Lớp 10 Toán 10 - Chân trời sáng tạo

Xác suất của biến cố sách CTST

1. Định nghĩa xác suất

Định nghĩa

Cho T là một phép thử ngẫu nhiên với không gian mẫu \Omega là một tập hữu hạn.

Giả sử A là một biến cố được mô tả bằng {{\Omega }_{A}}\subset \Omega. Xác suất của biến cố A, kí hiệu bởi P(A) cho bởi công thức:

P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}

Trong đó n(A) là số kết quả thuận lợi của biến cố A, n(\Omega) là số kết quả có thể xảy ra của phép thử (hay số phần tử không gian mẫu).

2. Tính chất của xác suất

Định lí

Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó ta có:

a) P\left( \emptyset \right) = 0;P\left( \Omega \right) = 1

b) 0 \leqslant P\left( A \right) \leqslant 1 với mọi biến cố A

Ví dụ: Hộp thứ nhất đựng 4 tấm thẻ cùng loại được đánh số từ 1 đến 4. Hộp thứ hai đựng 6 tấm thẻ cùng loại được đánh số từ 1 đến 6. Lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.

a) Hãy xác định không gian mẫu của phép thử

b) Gọi A là biến cố “Hai thẻ lấy ra có cùng số”. Hãy liệt kê các kết quả thuận lợi cho A và tính xác suất của biến cố A.

c) Gọi B là biến cố “Tổng hai số trên hai thẻ lấy ra lớn hơn 8”. Hãy liệt kê các kết quả thuận lợi cho B và tính xác suất của biến cố B.

Hướng dẫn giải

a) Kết quả của mỗi lần thử là một cặp (i; j) với i\in {1; 2; 3; 4} là số trên thẻ lấy ra từ hộp thứ nhất và j \in {1; 2; 3; 4; 5; 6} là số trên thẻ lấy ra từ hộp thứ hai. Không gian mẫu của phép thử là:

\Omega = \{(1;1); (1;2); 1; 3); (1; 4; (1; 5); (1; 6); 

(2; 1); (2; 2); (2; 3); 2; 4); (2; 5): (2; 6);

(3; 1); (3; 2); (3; 3); (3; 4); (3; 5); (3; 6),

(4; 1); (4; 2); (4; 3); (4; 4); (4; 5); (4: 6)\}

=> n(\Omega ) = 24

b) Không gian mẫu gồm có 24 kết quả, tức là n(\Omega ) = 24.

Biển cố A = \left \{ {(1; 1); (2; 2); (3; 3); (4; 4)} \right \}

Số các kết quả thuận lợi cho A là n(A) = 4.

Do đó, xác suất của biến cố A là:

P\left( A \right) = \frac{4}{{24}} = \frac{1}{6}

c) Biến cố B= \left \{ {(3; 6); (4; 5); (4; 6)}\right \}

Số các kết quả thuận lợi cho B là n(B) = 3.

Do đó, xác suất của biến cố B là

P\left( B \right) = \frac{3}{{24}} = \frac{1}{8}

3. Tính xác suất bằng sơ đồ hình cây

Trong chương VIII, chúng ta đã được làm quen với phương pháp sử dụng sơ đô hình cây để liệt kê các kết quả của một thí nghiệm. Ta cũng có thể sử dụng sơ đồ hình cây để tính xác suất

Ví dụ: Tung một đồng xu cân đối và đồng chất 3 lần liên tiếp. Tính xác suất của biến cố A: “Trong 3 lần tung có ít nhất 2 lần liên tiếp xuất hiện mặt sấp”.

Hướng dẫn giải

Kí hiệu S nếu tung được mặt sấp, N nếu tung được mặt ngửa. Các kết quả có thể xảy ra trong 3 lần tung được thể hiện ở sơ đồ hình cây như sau

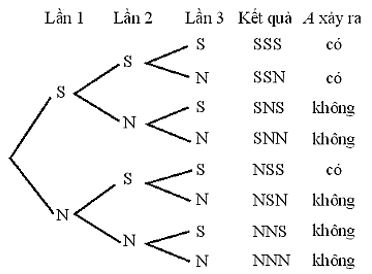
Toán 10 Bài 2: Xác suất của biến cố

Có tất cả 8 kết quả có thể xảy ra, trong đó có 3 kết quả thuận lợi cho A.

Do đó: P\left( A \right) = \frac{3}{8}

4. Biến cố đối

Giả sử A và B là hai biến cố liên quan đến một phép thử.

Định nghĩa

Tập Ω \setminus A được gọi là biến cố đối của biến cố A, kí hiệu \overline A

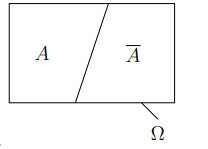
Xác suất của biến cố sách CTST

Chú ý: \overline A xảy ra khi và chỉ khi A không xảy ra.

Với mọi biến cố A ta có:

P\left( {\overline A } \right) = 1 - P\left( A \right)

Với {\overline A } là biến cố đối của biến cố A.

Ví dụ: Gieo đồng thời ba con xúc xắc cân đối và đồng chất. Gọi A là biến cố “Tích số chấm ở mặt xuất hiện trên ba con xúc xắc đó là số chẵn”

a) Hãy tìm biến cố đôi của biến cố A.

b) Hãy tính xác suất của biến cố A.

Hướng dẫn giải

a) Biến cố đối của biến cố A là biến cố “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc đó là số lẻ”,

b) Tổng số kết quả có thể xảy ra của phép thử là n\left( \Omega \right) = {6^3}.

\overline A xảy ra khi mặt xuất hiện trên cả ba con xúc xắc đều có số chấm là số lẻ. Số kết quả thuận lợi cho \overline A là n(\overline A ) = 33

Xác suất của biến cố \overline A là P\left( {\bar A{\rm{ }}} \right) = \frac{{{3^3}}}{{{6^3}}} = \frac{1}{8}

Xác suất của biến cố A là P\left( {A{\rm{ }}} \right) = 1 - P\left( {\overline {A{\rm{ }}} } \right) = \frac{7}{8}

5. Nguyên lí xác suất bé

Trong thực tế, các biến cố có xác suất xảy ra gần bằng 1 thì gần như là luôn xảy ra trong một phép thử. Ngược lại, các biến cố mà xác suất xảy ra gần bằng 0 thì gần như không xảy ra trong một phép thử.

Nguyên lí xác suất bé được phát biểu như sau:

Nếu một biến cố xác suất rất bé thì trong một phép thử, biến cố đó sẽ không xảy ra.

Ví dụ như khi một con tàu lưu thông trên biển, xác suất nó bị đâm là số dương. Tuy nhiên, nếu tuân thủ các quy tắc an toàn thì xác suất xảy ra biến cố này là rất nhỏ, con tàu có thể yên tâm hoạt động.

  • 14 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CTST