Lớp 10 Toán 10 - Chân trời sáng tạo

Các phép toán trên tập hợp sách CTST

1. Hợp và giao của các tập hợp

Cho hai tập hợp A và B. Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp A và B, kí hiệu là A \cup B

A \cup B = \left\{ {x|x \in A \text{ } \text{hoặc}\text{ } x\in B} \right\}

Hình vẽ minh họa

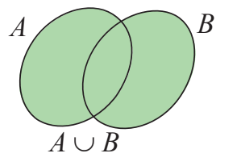
Hợp và giao của các tập hợp

Cho hai tập hợp A và B. Tập hợp các phần tử thuộc A và thuộc B gọi là giao của hai tập hợp A và B, kí hiệu là A \cap B

A \cap B = \left\{ {x|x \in A,x \in B} \right\}

Hình vẽ minh họa

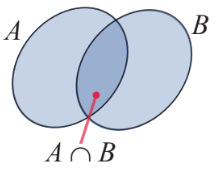
Hợp và giao của các tập hợp

Ví dụ: Cho hai tập hợp A = \left\{ {1;2;3;5;7} \right\}  và B = \{ n \in N|n là ước số của 12\}. Tìm A \cup B và A \cap B

Hướng dẫn giải

Ta có: B = \left\{ {1;2;3;4;6;12} \right\}

A \cap B = \left\{ {1;2;3} \right\}

A \cup B = \left\{ {1;2;3;4;5;6;7;12} \right\}

Nhận xét

Nếu A và B là hai tập hợp hữu hạn thì: 

  • n(A \cup B) = n(A) + n(B) - n(A \cap B)
  • Nếu A \cap B = \varnothing thì n(A \cup B) = n(A) + n(B)

Ví dụ: Lớp 10A có 15 bạn thích môn Văn, 20 bạn thích môn Toán. Trong số các bạn thích văn
hoặc toán có 8 bạn thích cả 2 môn. Trong lớp vẫn còn 10 bạn không thích môn nào trong 2 môn Văn và Toán. Hỏi lớp 10A có bao nhiêu bạn. 

Hướng dẫn giải

Sử dụng biểu đồ Ven để giải toán

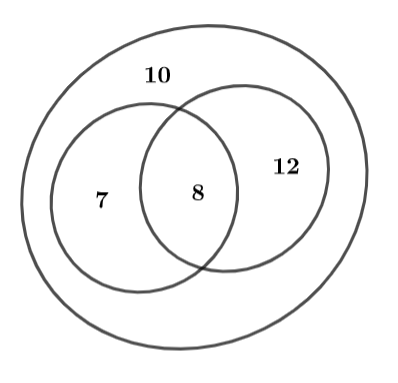
Các phép toán trên tập hợp

Ta có: Số bạn chỉ thích Văn là (bạn).

Số bạn chỉ thích Toán là 20 − 8 = 12 (bạn).

Số học sinh cả lớp là tổng các phần không giao nhau: 7 + 8 + 12 + 10 = 37.

Chú ý: Để tìm các tập hợp là hợp, giao, hiệu, phần bù của những tập con của tập số thực, ta thường sẽ vẽ sơ đồ trên trục số.

Ví dụ: Xác định các tập hợp sau đây bằng cách vẽ trục số:

a) (0; 3) ∪ (−3; 2)

b) A = \left \{ x ∈ \mathbb{R}||x +2| < 2 \right \} , B = \left \{ x ∈ \mathbb{R}||x +4| ≥ 3 \right \}. Tìm A∩B.

Hướng dẫn giải 

a) Biểu diễn tập hợp A trên trục số.

Biểu diễn tập B trên trục số.

Hình vẽ minh họa

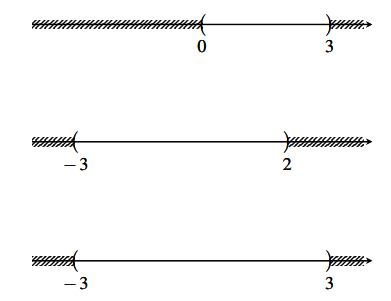
Các phép toán trên tập hợp

Kết hợp hai trục số trên ta được tập A∪B = (−3; 3)

b) Ta có: |x+2| < 2 ⇔ −2 < x+2 < 2 ⇔ −4 < x < 0

Do đó A = (−4; 0)|x+4| ≥ 3 

⇔ \left[ {\begin{array}{*{20}{l}} {x + 4 \leqslant - 3} \\ {x + 4 \geqslant 3} \end{array}} \right.

⇔ \left[ {\begin{array}{*{20}{l}} {x \leqslant - 7} \\ {x \geqslant - 1} \end{array}} \right.

Do đó B = (−∞;−7]∪[−1;+∞)

Biểu diễn tập A trên trục số

Biểu diễn tập B trên trục số

Hình vẽ minh họa

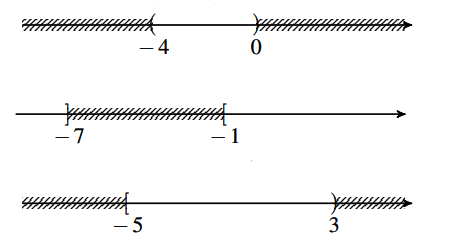
Các phép toán trên tập hợp

Biểu diễn tập C trên trục số => A \cap B = \left[ { - 5;3} \right)

2. Hiệu của hai tập hợp, phần bù của tập con

Cho hai tập hợp A và B. Tập hợp các phần tử thuộc A nhưng không thuộc B gọi là hiệu của hai tập hợp A và B, kí hiệu là A \setminus B.

A\setminus B = \left \{ x|x ∈ A \text{ }\text{và} \text{ } x ∉ B \right \}

Hình vẽ minh họa

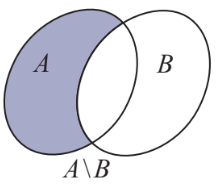
Hiệu của hai tập hợp, phần bù của tập con

Cho hai tập hợp A và E. Nếu A là tập con của E thì hiệu E\setminus A gọi là phần bù của A trong E, kí hiệu {C_E}A

Hình vẽ minh họa

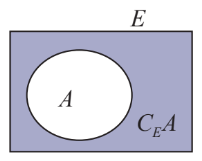
Hiệu của hai tập hợp, phần bù của tập con

Ví dụ: {C_\mathbb{Z}}\mathbb{N} = \mathbb{Z}{\rm{\backslash }}\mathbb{N} = \{ x|x \in \mathbb{Z} và x \notin \mathbb{N}\} = \{ ...; - 3; - 2; - 1\}

Đặc biệt: {C_S}S = \varnothing

Ví dụ: Xác định tập hợp (0; 3) \setminus (2; 4) và biểu diễn chúng trên trục số.

Hướng dẫn giải

Để xác định tập hợp ta biểu diễn trục số như sau:

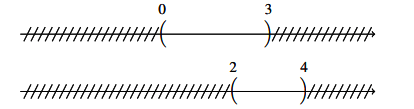
Các phép toán trên tập hợp

=> (0; 3)\setminus (2; 4) = (0; 2]

Ví dụ: Cho hai tập hợp A = \left \{ x ∈ \mathbb{R}|1 < x ≤ 4 \right \} , B = \left \{ x ∈ \mathbb{R}| −3 < x \right \}. Tìm C_BA.

Hướng dẫn giải

Để xác định tập hợp ta biểu diễn trục số như sau:

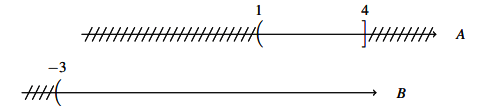
Các phép toán trên tập hợp

=> C_BA = (−3; 1]∪(4;+∞)

Câu trắc nghiệm mã số: 21019,21014,21003,21001
  • 31 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CTST