Lớp 10 Toán 10 - Chân trời sáng tạo

Giải tam giác và ứng dụng thực tế sách CTST

A. Giải tam giác

Định nghĩa

Giải tam giác là tìm số đo các cạnh và các góc chưa biết của tam giác.

Để giải tam giác ta thường sử dụng một cách hợp lí các hệ thức lượng như định lí sin, định lí cosin và các công thức tính diện tích tam giác.

Định lí cosin

Trong tam giác ABC:

\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}

Định lí sin

Trong tam giác ABC với BC=a,CA=b,AB=c ta có:

\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.

(R là bán kính đường tròn ngoại tiếp tam giác ABC)

Các công thức tính diện tích tam giác

  • \ S = \frac{1}{2}a{h_a} = \frac{1}{2}b{h_b} = \frac{1}{2}c{h_c}
  • \ S = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B = \frac{1}{2}ab\sin C
  • \ S = \frac{{abc}}{{4R}}
  • \ S = pr = \frac{{(a + b + c).r}}{2}
  • \ S = \sqrt {p(p - a)(p - b)(p - c)} (Công thức Heron)

Ví dụ:  Cho tam giác ABC có AC = 10cm, BC = 16 cm và C = 120^0, tính độ dài cạnh AB.

Hướng dẫn giải

Áp dụng định lí cosin ta có:

\begin{matrix} A{B^2} = C{A^2} + C{B^2} - 2CA.CB.\cos \widehat C \hfill \\ \Rightarrow AB = \sqrt {516} \left( {cm} \right) \hfill \\ \end{matrix}

B. Áp dụng giải tam giác vào thực tế

Ví dụ: Người ta dự định xây một cây cầu bắc qua một con sông tương đối rộng và chảy xiết. Trong một đợt khảo sát người ta muốn đo khoảng cách giữa hai điểm A và B ở hai bên bờ sông. Khó khăn là người ta không thể qua sông bằng bất kì phương tiện gì. Em hãy đặt mình vào vị trí của người khảo sát để giải quyết tình huống này. Biết rằng em có dụng cụ ngắm đo góc và thước dây.

Hướng dẫn giải

Hình vẽ minh họa

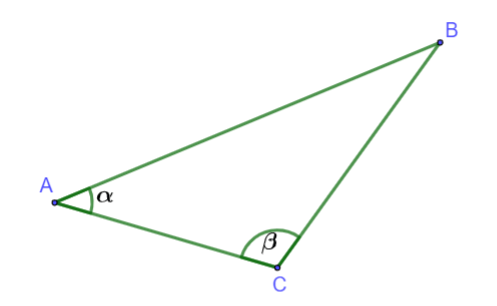
Giải tam giác và ứng dụng thực tế

Để tính được chiều dài AB ta sẽ tạo một tam giác mà có AB là một cạnh.

Ta chọn điểm C nằm bên bờ (có thể cùng phía với A hoặc với B) và ta xem trong tam giác này ba yếu tố nào ta đo được bằng các dụng cụ đã có.

Giả sử điểm C nằm cùng bờ với điểm A như hình vẽ. Các yếu tố đo được là cạnh AC và hai góc \widehat {BAC} = \alpha ,\widehat {ACB} = \beta

Áp dụng định lí sin trong tam giác ABC ta có:

\frac{{AB}}{{\sin \beta }} = \frac{{AC}}{{\sin \left( {\alpha + \beta } \right)}}

\Leftrightarrow \frac{{AB}}{{\sin \beta }} = \frac{{AC}}{{\sin \left( {\alpha + \beta } \right)}}

Ví dụ: Một hành khách ngồi trong một máy bay, bay ở độ cao 10km nhìn xuống hai thị trấn dưới mặt đất. Góc hợp bởi phương ngang và hai thị trấn lần lượt là 28^0 và 55^0 (hình vẽ). Tính khoảng cách giữa hai thị trấn.

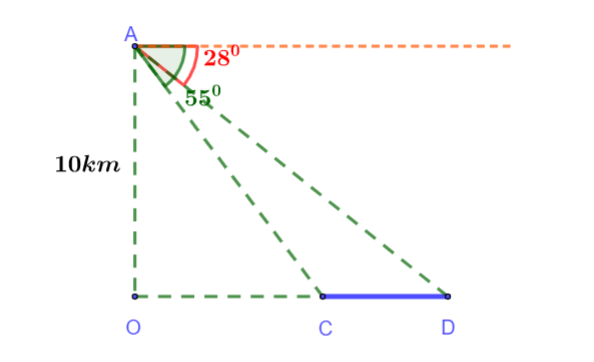
Giải tam giác và ứng dụng thực tế

Hướng dẫn giải

Ta có: \widehat {CAD} = {55^0} - {28^0} = {27^0}

Xét tam giác ACO ta có: 

\widehat {OAC} = {90^0} - {55^0} = {35^0}

\cos \widehat {OAC} = \frac{{AO}}{{AC}}

\Leftrightarrow AC = \frac{{10}}{{\cos {{35}^0}}} \approx 12,2km

Trong tam giác ACD ta có:

\widehat {ACD} = {180^0} - \widehat {OAC} = {125^0}

\Rightarrow \widehat {ADC} = {180^0} - \left( {{{125}^0} + {{27}^0}} \right) = {28^0}

Áp dụng định lý sin trong tam giác ACD, ta có:

\frac{{CD}}{{\sin {{27}^0}}} = \frac{{AC}}{{\sin {{28}^0}}}

\Leftrightarrow CD = \frac{{AC.\sin {{27}^0}}}{{\sin {{28}^0}}} \approx 11,79km

Vậy khoảng cách giữa hai thị trấn khoảng 11,9km.

Câu trắc nghiệm mã số: 21717,21718,21719
  • 33 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CTST