Lớp 10 Toán 10 - Cánh diều

Dấu của tam thức bậc hai

Dấu của tam thức bậc hai

  • Tam thức bậc hai là biểu thức có dạng f(x)=a{{x}^{2}}+bx+c(a\ne 0), a,b,c được gọi là các hệ số.
  • Nghiệm của phương trình bậc hai a{{x}^{2}}+bx+c=0 cũng được gọi là nghiệm của tam thức bậc hai a{{x}^{2}}+bx+c.

Cho tam thức bậc hai f(x)=a{{x}^{2}}+bx+c(a\ne 0). Ta có:

  • Nếu \Delta <0 thì f(x) cùng dấu với hệ số a với mọi x thuộc \mathbb{R}.
  • Nếu \Delta =0 thì f(x) cùng dấu với hệ số a với mọi x\ne -\frac{b}{2a} và f\left( -\frac{b}{2a} \right)=0.
  • Nếu \Delta >0 thì f(x) có hai nghiệm phân biệt {{x}_{1}};{{x}_{2}}({{x}_{1}}<{{x}_{2}}). Khi đó: f(x) cùng dấu với hệ số a với mọi x\in \left( -\infty ;{{x}_{1}} \right)\cup \left( {{x}_{2}};+\infty \right); f(x) trái dấu với hệ số a với mọi x\in \left( {{x}_{1}};{{x}_{2}} \right).

(Trong định lý trên, có thể thay \Delta bằng \Delta ').

Ví dụ:

Xét dấu các tam thức bậc hai sau:

a. {{x}^{2}}+x+2;

b. 2{{x}^{2}}+x-3.

Hướng dẫn giải

a. f(x)={{x}^{2}}+x+2 có \Delta =-7<0 và a=1>0 nên f(x)>0\,\,\forall x\in R.

b. g(x)=2{{x}^{2}}+x-3 có \Delta =25>0, a=2>0. g(x) có hai nghiệm phân biệt {x}_{1}=1,{x}_{2}=-\frac{3}{2}.

Bảng xét dấu:

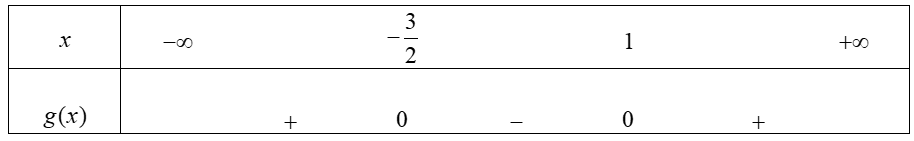
Suy ra g(x)>0\,\,\forall x\in \left( -\infty ;-\frac{3}{2} \right)\cup \left( \frac{3}{2};+\infty \right) và g(x)<0\,\,\forall x\in \left( -\frac{3}{2};1 \right).

 

  • 6 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CD