Quy tắc cộng, quy tắc nhân. Sơ đồ hình cây

1. Sơ đồ hình cây

Xét một ví dụ:

Trong một cửa hàng có hai loại kem: Kem que và kem ốc quế. Có 3 loại kem que là Kem sữa dừa, kem đậu xanh và kem ca cao. Có 4 loại kem ốc quế là kem vani, kem ca cao, kem sữa dừa và kem dâu. Hỏi có bao nhiêu cách chọn mua 1 cây kem?

Hướng dẫn giải

Ta có sơ đồ:

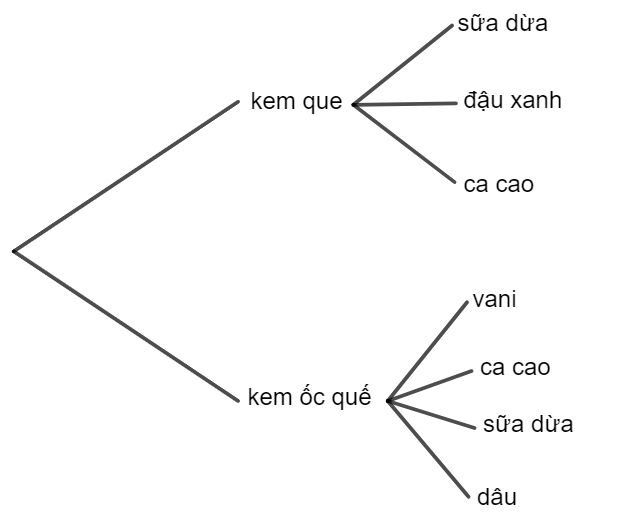
Nhận xét: có 7 cách chọn mua 1 cây kem (có 3 cách chọn kem que, 4 cách chọn kem ốc quế).

2. Quy tắc cộng

Chú ý:

• Quy tắc cộng có thể mở rộng cho công việc có nhiều hơn hai phương án.
• Ta áp dụng quy tắc cộng cho một công việc có nhiều phương án, các phương án đó phải tách rời nhau, độc lập với nhau (không trùng lặp).

Ví dụ: Một nhà hàng có 3 loại rượu, 4 loại bia và 6 loại nước ngọt. Thực khách cần chọn đúng 1 loại thức uống. Hỏi có mấy cách chọn?

Hướng dẫn giải

Thực khách có 3 phương án có thể chọn một đồ uống: rượu, bia, nước ngọt.

Rượu có 3 loại, bia có 4 loại, nước ngọt có 6 loại.

Do đó, áp dụng quy tắc cộng, số cách chọn một đồ uống là: 3+4+6 = 13 (cách).

3. Quy tắc nhân

Chú ý:

• Quy tắc nhân có thể mở rộng cho công việc có nhiều hơn hai công đoạn.
• Ta áp dụng quy tắc nhân cho công việc có nhiều công đoạn, các công đoạn nối tiếp nhau nhưng các công đoạn phải độc lập với nhau (không trùng lặp).

Ví dụ 1: Giữa thành phố A và thành phố B có 3 loại phương tiện giao thông. Giữa thành phố B và thành phố C có 4 loại phương tiện giao thông. Hỏi có bao nhiêu cách đi từ thành phố A đến thành phố C, biết rằng bắt buộc phải đi qua thành phố B mới đến được thành phố C.

Hướng dẫn giải

Công việc đi từ thành phố A đến thành phố C có 2 công đoạn.

Công đoạn 1: Đi từ A đến B có 3 cách chọn phương tiện.

Công đoạn 2: Đi từ B đến C có 4 cách chọn phương tiện.

Do đó, áp dụng quy tắc nhân, ta có: 3.4 = 12 (cách) đi từ thành phố A đến thành phố C.

Ví dụ 2: Từ các chữ số của tập A = {1; 2 ; 3; 4; 5}, có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số đôi một khác nhau và số đó là số lẻ ?

Hướng dẫn giải

Gọi số cần lập có dạng: .

Vì là số lẻ nên có 3 cách chọn (đó là 1; 3; 5).

có 4 cách chọn (vì tập A có 5 số, bỏ đi 1 số do chọn).

có 3 cách chọn (vì tập A có 5 số, bỏ đi 1 số do chọn, bỏ đi 1 số do chọn).

Do đó, áp dụng quy tắc nhân, ta có: 3.4.3 = 36 (số) thỏa mãn số tự nhiên gồm 3 chữ số đôi một khác nhau và số đó là số lẻ.

4. Kết hợp quy tắc cộng và nhân

Ở 2 ví dụ trên, chúng ta chỉ áp dụng 1 quy tắc đếm. Tuy nhiên, hầu hết các bài toán đếm trong thực tế thường phải áp dụng kết hợp cả 2 quy tắc.

Ví dụ: Một đội học sinh giỏi của trường THPT gồm 5 học sinh khối 12, 4 học sinh khối 11, 3 học sinh khối 10. Số cách chọn hai học sinh trong đó mỗi khối có một em là bao nhiêu?

Hướng dẫn giải

Trường hợp 1: Chọn 1 học sinh khối 10, 1 học sinh khối 11.

• Chọn 1 học sinh khối 10: có 3 cách
• Chọn 1 học sinh khối 11: có 4 cách

Áp dụng quy tắc nhân, số cách chọn 1 học sinh khối 10, 1 học sinh khối 11 là : 3.4 = 12 (cách).

Trường hợp 2: Chọn 1 học sinh khối 11, 1 học sinh khối 12.

• Chọn 1 học sinh khối 11: có 4 cách
• Chọn 1 học sinh khối 12: có 5 cách

Áp dụng quy tắc nhân, số cách chọn 1 học sinh khối 11, 1 học sinh khối 12 là : 4.5 = 20 cách.

Trường hợp 3: Chọn 1 học sinh khối 12, 1 học sinh khối 10.

• Chọn 1 học sinh khối 12: có 5 cách.
• Chọn 1 học sinh khối 10: có 3 cách.

Áp dụng quy tắc nhân, số cách chọn 1 học sinh khối 12, 1 học sinh khối 10 là : 5.3 = 15 cách.

Vậy, áp dụng quy tắc cộng, có (12+20+15) = 47 cách chọn hai học sinh trong đó mỗi khối có một em.