Lớp 10 Toán 10 - Cánh diều

Hệ bất phương trình bậc nhất hai ẩn

1. Khái niệm hệ bất phương trình bậc nhất hai ẩn

  • Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
  • Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.
  • Trên mặt phẳng tọa độ Oxy, tập hợp các điểm (x_0;y_0) có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của hệ bất phương trình đó.

Ví dụ: Cho hệ bất phương trình \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {2x + y > 0}\\ {x - 3y < 1} \end{array}}\\ {x \ge 2} \end{array}} \right.. Các cặp số sau đây có phải là nghiệm của hệ bất phương trình này hay không?

a) (x;y)=(0;0);

b) (x;y)=(3;4).

Hướng dẫn giải

a) Vì 2.0+0=0 không thỏa mãn bất phương trình số (1) nên cặp số (0;0) không là nghiệm của hệ bất phương trình.

b) Vì \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {2.3 + 4 = 10 > 0}\\ {3 - 3.4 = - 9 < 1} \end{array}}\\ {3 \ge 2} \end{array}} \right. thỏa mãn cả 3 bất phương trình nên cặp số (3;4) là nghiệm của hệ bất phương trình.

2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn

  • Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn, ta thực hiện như sau:
  • Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.
  • Miền không bị gạch còn sót lại là miền nghiệm của hệ bất phương trình đã cho.

Ví dụ: Biểu diễn miền nghiệm của hệ bất phương trình: \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {x \ge 0}\\ {y \ge 0}\\ {3x + y \le 6} \end{array}}\\ {x + y \le 4} \end{array}} \right..

Hướng dẫn giải

Xác định miền nghiệm của bất phương trình x \ge 0 là nửa mặt phẳng nằm bên phải trục tung, tính cả trục Oy. Gạch bỏ phần còn lại không phải là nghiệm.

Xác định miền nghiệm của bất phương trình y \ge 0 là nửa mặt phẳng nằm trên trục hoành, tính cả trục Ox. Gạch bỏ phần còn lại không phải là nghiệm.

Xác định miền nghiệm của bất phương trình 3x+y \le 6:

Vẽ đường thẳng d: 3x+y=6.

Xét điểm O(0;0) \notin d. Vì 3.0+0=3<6 nên nửa mặt phẳng chứa điểm O tính cả bờ d là miền nghiệm của bất phương trình 3x+y \le 6. Gạch bỏ phần còn lại không phải là nghiệm.

Tương tự, xác định miền nghiệm của bất phương trình x+y \le 4, sau đó gạch bỏ phần còn lại không phải là nghiệm.

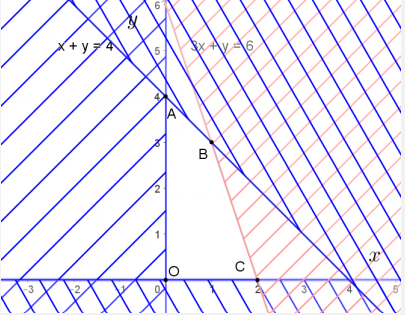
Miền không bị gạch còn sót lại chính là miền nghiệm của hệ bất phương trình ban đầu. Đó chính là tứ giác OABC (tính cả các cạnh của tứ giác).

3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F=Ax+By trên một miền đa giác

  • Hệ bất phương trình giúp mô tả được nhiều bài toán thực tế để tìm ra cách giải quyết tối ưu. Chúng thường được đưa về bài toán tìm giá trị lớn nhất (GTLN) hoặc giá trị nhỏ nhất (GTNN) của biểu thức F=Ax+By trên một miền đa giác.
  • Người ta chứng minh được F đạt GTLN hoặc GTNN tại một trong các đỉnh của đa giác.

Ví dụ: Anh Tú muốn trồng hoa hồng và hoa cúc trên mảnh vườn diện tích bằng 8 hecta để bán lấy tiền. Nếu trồng 1 hecta hoa hồng thì cần 20 ngày công đồng thời thu được 40 triệu đồng. Còn nếu trồng 1 hecta hoa cúc thì cần 30 ngày công đồng thời thu được 50 triệu đồng. Hỏi anh Tú cần trồng bao nhiêu hecta hoa mỗi loại để thu được số tiền lớn nhất? Biết rằng anh Tú chỉ có thể sử dụng tối đa 180 ngày công.

Hướng dẫn giải

Gọi x là số hecta trồng hoa hồng, y là số hecta trồng hoa cúc. Suy ra x \ge 0;y \ge0.

Diện tích mảnh vườn bằng 8 ha nên x+y \le 8.

Số ngày công huông vượt quá 180 nên 20x+30y \le 180.

Vậy ta có hệ bất phương trình: \left\{ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{x + y \le 8}\end{array}}\\{20x + 30y \le 180}\end{array}} \right.

Biểu diễn miền nghiệm của hệ này, ta được miền tứ giác OABC.

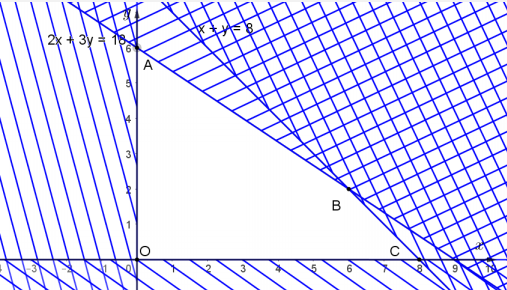
Bốn đỉnh của tứ giác có tọa độ O(0;0);A(0;6);B(6;2);C(8;0).

Gọi F là số tiền thu được khi bán sản phẩm (đơn vị triệu đồng). Ta có: F=40x+50y.

Giá trị lớn nhất của F sẽ đạt được tại một trong bốn đỉnh đa giác OABC.

Tính giá trị của biểu thức F=40x+50y tại các đỉnh OABC, ta có:

  • Tại O(0;0): F=40.0+50.0=0.
  • Tại A(0;6): F=40.0+50.6=300.
  • Tại B(6;2): F=40.6+50.2=340.
  • Tại C(8;0): F=40.8+50.0=320.

Do đó, F đạt giá trị lớn nhất bằng 340 tại B(6;2).

Vậy để thu được số tiền lớn nhất, anh Tú cần trồng 6 ha hoa hồng và 2 ha hoa cúc.

 

 

 

  • 13 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CD