Giải tam giác

1. Các công thức tính diện tam giác

Cho tam giác $ABC$ , ta kí hiệu:

$AB=c,BC=a,CA=b$ ;
$h_a,h_b,h_c$ lần lượt là độ dài các đường cao kẻ từ $A,B,C$ ;
$R$ là bán kính đường tròn ngoại tiếp;
$r$ là bán kính đường tròn nội tiếp;
$p= \frac{a+b+c}2$ là nửa chu vi;
$S$ là diện tích tam giác $ABC$ .

Ta có các công thức tính diện tích tam giác sau:

$S_{ABC}=\frac12 a.h_a=\frac12 b.h_b =\frac12 c.h_c$ ;
$S_{ABC}=\frac12bc\sin A=\frac12ac\sin B=\frac12ab\sin C$ ;
$S_{ABC}=\frac {abc}{4R}$ ;
$S_{ABC}=p.r$ ;
$S_{ABC}=\sqrt{p(p-a)(p-b))p-c)}$ (Công thức Heron).

Ví dụ 1: Cho tam giác $ABC$ có $a=5,b=6,c=7$ . Tính diện tích tam giác $ABC$ .

Hướng dẫn giải

(Khi biết 3 cạnh của tam giác, ta sử dụng công thức Heron)

Ta có: $p=\frac{a+b+c}2=\frac{5+6+7}2=9$ .

Áp dụng công thức Heron:

$S_{ABC}=\sqrt{p(p-a)(p-b))p-c)}$ $=\sqrt{9(9-5)(9-6)(9-7)} = 6\sqrt6$ .

Ví dụ 2: Cho tam giác $ABC$ có $c=3,b=4,\hat A=120^{\circ}$ . Tính diện tích tam giác này.

Hướng dẫn giải

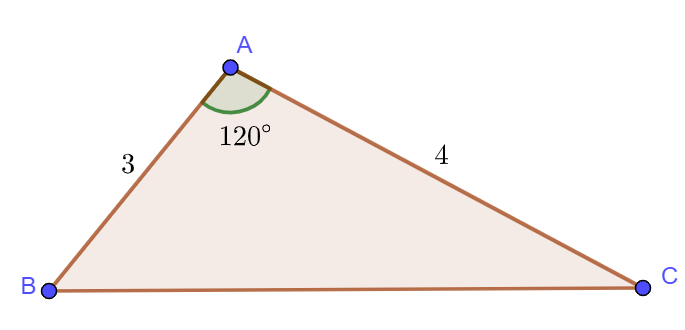
(Khi biết 2 cạnh và 1 góc xen giữa, ta sử dụng công thức số 2)

Ta có: $S_{ABC}=\frac12bc\sin A=\frac12.3.4\sin 120^{\circ} =3\sqrt3$ .

2. Giải tam giác

Giải tam giác là đi tìm số đo tất cả các cạnh và tất cả các góc của tam giác.

Ví dụ: Giải tam giác $ABC$ biết $a=4,\hat B=60^{\circ} ,\hat C=45^{\circ}$ .

Hướng dẫn giải

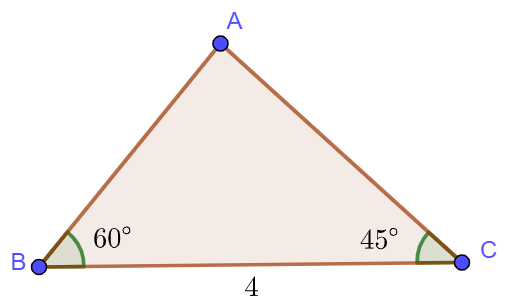
Ta có: $\hat A=180^{\circ} -(\hat B+\hat C)$ $=180^{\circ} -(60^{\circ} +45^{\circ} )=75^{\circ}$ .

Áp dụng định lý sin, ta có: $\frac{4}{\sin 75^{\circ} }=\frac b{\sin 60^{\circ}}=\frac c{\sin45^{\circ}}=2R$ .

Suy ra: $b=\sin 60^{\circ} .\frac 4{\sin 75^{\circ} } \approx 3,59$ , $x=\sin 45^{\circ} .\frac 4{\sin 75^{\circ} } \approx =2,93$ , $R=\frac 4{2\sin 75^{\circ} } \approx 2,07$ .

9 lượt xem

Sắp xếp theo

Xóa Gửi bình luận

Toán 10 CD