Tọa độ của vectơ
1. Tọa độ của vectơ
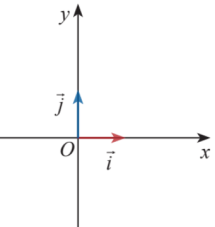
Cho hệ trục ![]() , ta có:
, ta có:
- Vectơ đơn vị của trục hoành là

- Vectơ đơn vị của trục tung là

- Với mỗi vectơ
 , ta luôn có:
, ta luôn có:  . Trong đó
. Trong đó  được gọi là hoành độ, tung độ của
được gọi là hoành độ, tung độ của  .
. - Cho hai điểm
 và
và  , khi đó
, khi đó  .
. - Hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau, tức là:
![]()
- Nếu điểm
 có tọa độ
có tọa độ  thì vectơ
thì vectơ 
Ví dụ 1: Trong mặt phẳng tọa độ ![]() , cho
, cho ![]() . Tìm
. Tìm ![]() sao cho tứ giác
sao cho tứ giác ![]() là hình bình hành.
là hình bình hành.
Hướng dẫn giải
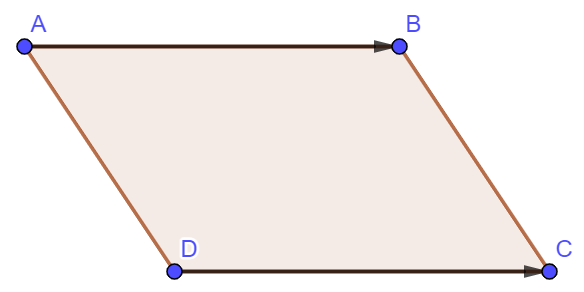
Vì tứ giác ![]() là hình bình hành nên
là hình bình hành nên ![]() .
.
Áp dụng công thức tính tọa độ vectơ khi biết hai điểm, ta có: ![]() và
và ![]() .
.
Ta có:![]()
![]()
![]() .
.
Vậy ![]() .
.
Ví dụ 2: Tìm tọa độ các vectơ sau:
a) ![]()
b) ![]()
Hướng dẫn giải
a) Ta có: ![]() .
.
b) Ta có: ![]() .
.
Ví dụ 3: Trong mặt phẳng tọa độ ![]() , cho điểm
, cho điểm ![]() . Tìm tọa độ điểm đối xứng của
. Tìm tọa độ điểm đối xứng của ![]() qua trục
qua trục ![]() và
và ![]() .
.
Hướng dẫn giải
Biểu diễn điểm ![]() lên hệ trục tọa độ và lấy các điểm đối xứng của
lên hệ trục tọa độ và lấy các điểm đối xứng của ![]() .
.
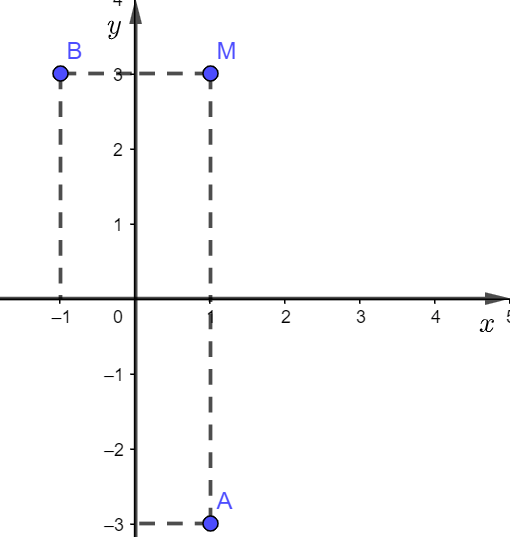
Vậy điểm đối xứng của ![]() qua trục
qua trục ![]() là điểm
là điểm ![]() .
.
Điểm đối xứng của ![]() qua trục
qua trục ![]() là điểm
là điểm ![]() .
.
Sắp xếp theo
Xóa
Gửi bình luận
-
Chương 1: Mệnh đề toán học. Tập hợp
-
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
-
Chương 3: Hàm số và đồ thị
-
Chương 4: Hệ thức lượng trong tam giác. Vectơ
-
Đề thi học kì 1
-
Chương 5: Đại số tổ hợp
-
Đề thi giữa học kì 2
-
Chương 6: Một số yếu tố thống kê và xác suất
-
Chương 7: Phương pháp tọa độ trong mặt phẳng
-
Đề thi học kì 2







