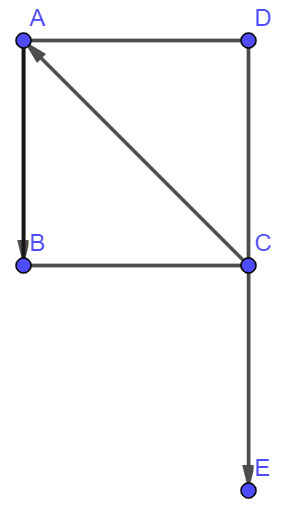
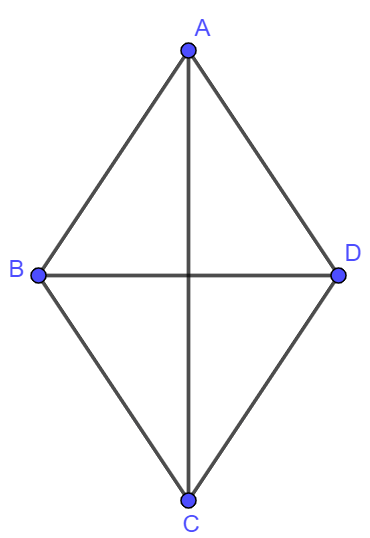
Biết ![]() và
và ![]() . Câu nào sau đây đúng?
. Câu nào sau đây đúng?
Hướng dẫn:
Ta có: .
Suy ra và
ngược hướng.