Trắc nghiệm Toán 10 Chương 2 Bài 1: Bất phương trình bậc nhất hai ẩn

 Thay (0; 1) vào bất phương trình, ta được: 1 < 1 (sai). Do đó cặp số này không là nghiệm của bất phương trình.

Ta có: .

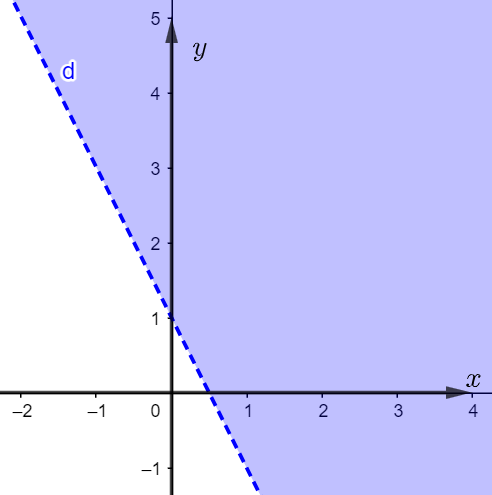
 Đường thẳng d đi qua hai điểm và nên nó là đường thẳng

Xét điểm . Thay tọa độ vào d ta được: . Suy ra miền tô đậm (không chứa d) là miền nghiệm của bất phương trình .

 Thay điểm (4; 2) vào bất phương trình, ta được: 14 < 10 (sai). Do đó điểm này không thuộc miền nghiệm của bất phương trình.

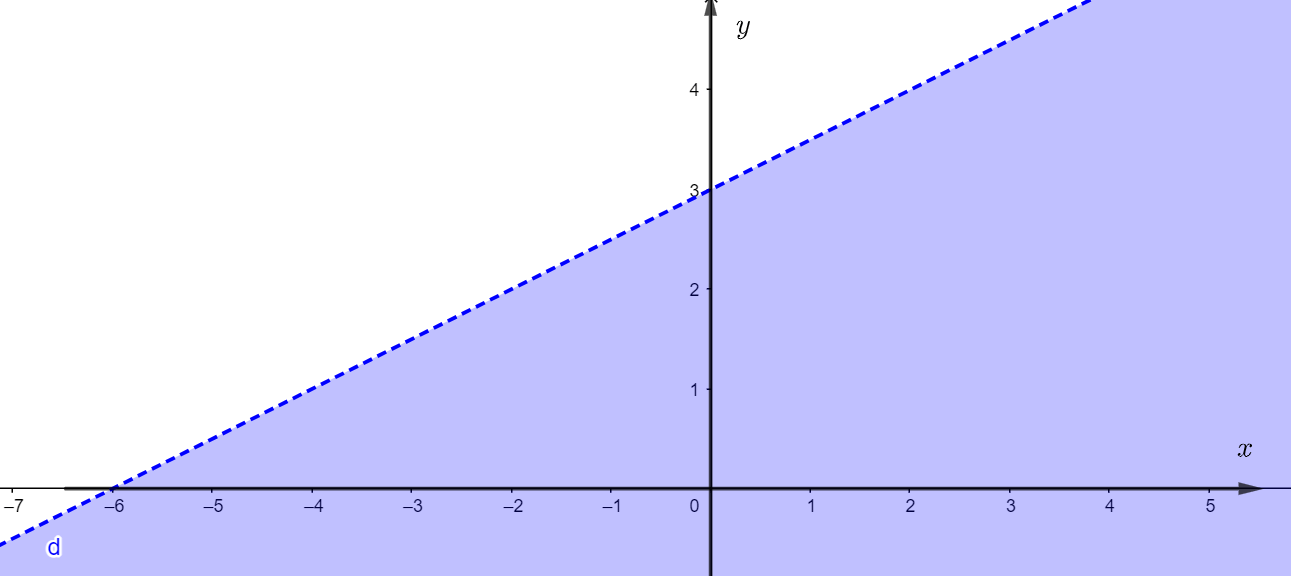
 Đường thẳng d đi qua 2 điểm và nên nó có dạng: .

Xét điểm , thay vào d ta được: . Suy ra miền tô đậm (chứa O) là miền nghiệm của bất phương trình .

 Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

 Thay cặp số (1; – 1) vào bất phương trình ta được: thỏa mãn. Suy ra cặp số này là nghiệm của bất phương trình.

 Bất phương trình bậc nhất hai ẩn là:

 Thay điểm O(0;0) thuộc phần tô đậm vào bất phương trình , ta được: (loại).

Thay điểm (-4;1) thuộc phần tô đậm vào bất phương trình ta được:  (loại).

Thay điểm (-5;1) thuộc phần tô đậm vào bất phương trình ta được: (loại).

Vậy chọn