Lớp 10 Toán 10 - Cánh diều

Tập hợp. Các phép toán trên tập hợp

1. Khái niệm tập hợp

a. Tập hợp và phần tử

Trong toán học, người ta thường dùng từ tập hợp để chỉ một nhóm đối tượng nào đó hoàn toàn xác định. Mỗi đối tượng trong nhóm gọi là một phần tử của tập hợp đó.

Ví dụ: 

+ Các học sinh lớp 10B tạo thành một tập hợp.

+ Phương trình x^2-9=0 có hai nghiệm x=\pm 3. Các nghiệm này tạo thành tập hợp nghiệm của phương trình trên. Tập hợp này có hai phần tử là x=3 và x=-3.

Người ta thường kí hiệu tập hợp bằng các chữ cái in hoa, kí hiệu phần tử bằng các chữ cái in thường.

Giả sử cho trước tập A. Kí hiệu:

  • a \in A: phần tử a thuộc tập A.
  • a \notin A: phần tử a không thuộc tập A.

b. Các cách xác định tập hợp

Thường có hai cách để cho một tập hợp:

  • Liệt kê

Ví dụ: A=\{2;4;6;8\}.

  • Chỉ ra tính chất đặc trưng

Ví dụ 1: Tập hợp A các nghiệm của phương trình x^2+2x-3=0 được viết là B=\{x \in \mathbb{R}|x^2+2x-3=0\}.

Ví dụ 2: Hãy viết tập hợp sau bằng cách nêu tính chất đặc trưng:

A=\{0;2;4;6;8;10\}.

Hướng dẫn giải

Các phần tử thuộc tập A là các số chia hết cho 2 và nhỏ hoặc bằng 10 nên ta có:

A=\{x|x \vdots2,x \le10\}.

c. Tập hợp rỗng

Là tập hợp không chứa phần tử nào. Kí hiệu: \varnothing.

Ví dụ: Tập  A= \{x \in \mathbb{N}| x^2-3=0\} có phải là tập hợp rỗng hay không?

Hướng dẫn giải

Ta có: x^2-3=0 \Leftrightarrow x=\pm \sqrt3 (loại vì x \in \mathbb{N}).

Vậy tập A không chứa phần tử nào nên nó là tập rỗng.

d. Số phần tử của một tập hợp

Nếu tập A là tập hợp hữu hạn phần tử thì số phần tử của A được kí hiệu là n(A).

Ví dụ: A=\{1;2;3\} \Rightarrow n(A)=3.

 

2. Tập con và tập hợp bằng nhau

a. Tập con

Tập A được gọi là tập con của tập B nếu mọi phần tử của A đều là phần tử của B.

  • Kí hiệu: A \subset B.
  • Như vậy: A \subset B \Leftrightarrow \forall x,x \in A \Rightarrow x \in B.

Nhận xét:

  • A \subset A và \varnothing \subset A với mọi tập A.
  • Nếu A \subset B,B \subset C \Rightarrow A \subset C.
  • Nếu A không là tập con của B thì kí hiệu A \not\subset B.

Biểu đồ Ven minh họa tập A là tập con của tập B:

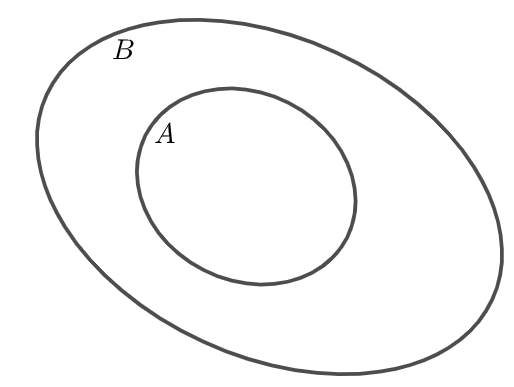
b. Tập hợp bằng nhau

Khi A \subset B và B \subset A thì ta nói tập hợp A bằng tập hợp B.

  • Kí hiệu A=B.
  • Như vậy, A=B \Leftrightarrow \forall x,x\in A \Rightarrow x \in B.

Ví dụ: Cho A=\{3;4\};B=\{3;x\};C=\{y;4\}. Tìm x và y để A=B=C.

Hướng dẫn giải

Để A=B=C thì các phần tử của ba tập hợp này phải giống nhau. Do đó x=4;y=3.

3. Một số tập con của tập số thực \mathbb{R}

Tập số thực (-\infty;+\infty) = \mathbb{R}

Đoạn [a;b]=\{x \in \mathbb{R}|a\le x \le b\}

Khoảng (a;b)=\{x \in \mathbb{R}|a< x < b\}

Nửa khoảng [a;b)=\{x \in \mathbb{R}|a\le x < b\}

Nửa khoảng (-\infty;a] =\{x \in \mathbb{R}| x\le a \}

Nửa khoảng [a;+\infty)=\{x \in \mathbb{R}|x \ge a\}

Khoảng (-\infty;a) =\{x \in \mathbb{R}| x< a \}

Khoảng (a;+\infty)=\{x \in \mathbb{R}|x > a\}

4. Các phép toán trên tập hợp

a. Phép giao

  • Giao của hai tập hợp A và B, kí hiệu là A \cap B. 
  • Là tập hợp bao gồm các phần tử thuộc cả A và B.
  • A \cap B=\{x,x\in A và x\in B \}.

Biểu đồ Ven minh họa A \cap B

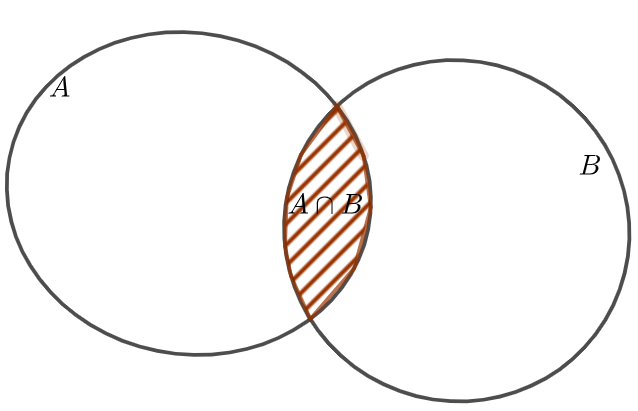
Ví dụ 1: Cho tập A=\{0;1;2;3;4\} và B=\{2;3;4;5\}. Tìm tập hợp A \cap B.

Hướng dẫn giải

Ta có: A \cap B = \{2;3;4\}.

Ví dụ 2: Xác định tập hợp và biểu diễn trên trục số: [-2;1) \cap (0;4].

Hướng dẫn giải

Ta có: [-2;1) \cap (0;4] =(0;1).

Biểu diễn trên trục số

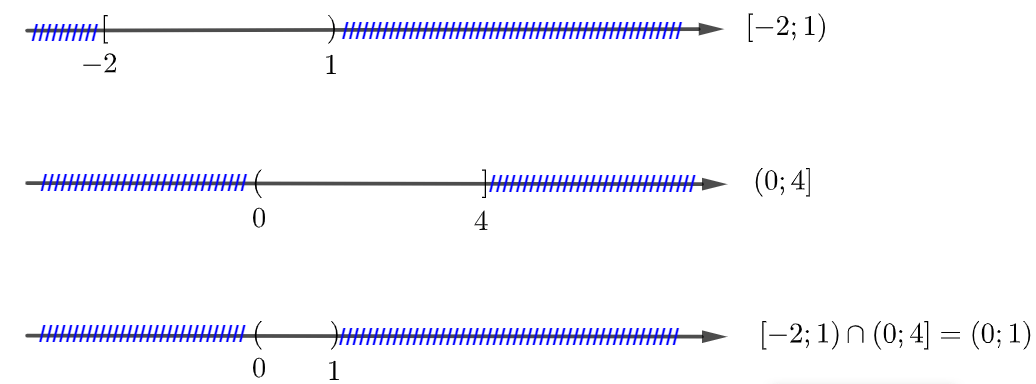
b. Phép hợp

  • Hợp của hai tập hợp A và B, kí hiệu là A\cup B.
  • Là tập hợp bao gồm tất cả các phần tử thuộc A hoặc thuộc B.
  • A \cup B= \{x|x\in A hoặc x \in B \}.

Biểu đồ Ven minh họa A \cup B

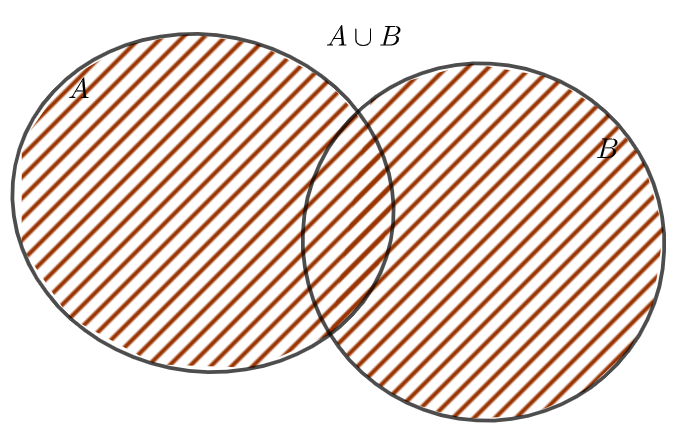
Ví dụ 1: Cho tập A=\{0;1;2;3;4\} và tập B=\{2;3;4;5\}. Tìm tập hợp A \cup B.

Hướng dẫn giải

Ta có: A \cup B =\{0;1;2;3;4;5\}.

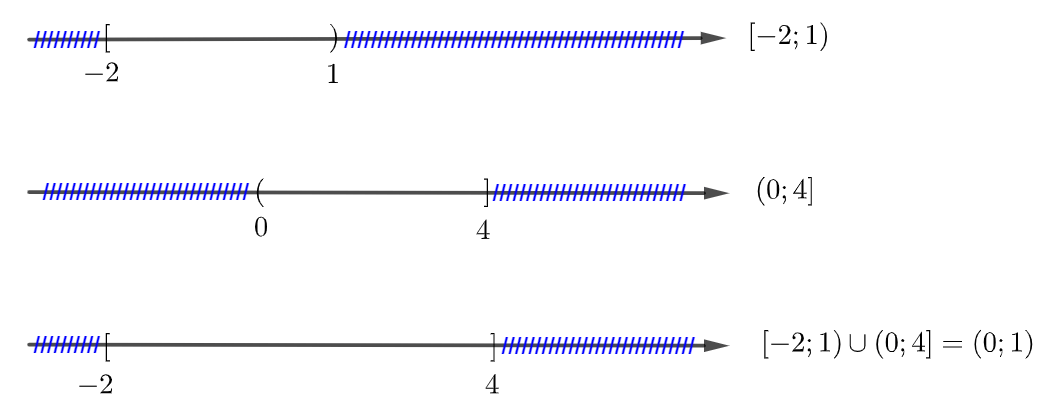
Ví dụ 2: Xác định tập hợp và biểu diễn trên trục số: [-2;1) \cup (0;4].

Hướng dẫn giải

Ta có: [-2;1) \cap (0;4] =[-2;4].

Biểu diễn trên trục số

c. Phép hiệu

  • Hiệu của hai tập hợp A và B, kí hiệu là A \setminus B.
  • Là tập hợp bao gồm những phần tử thuộc A nhưng không thuộc B.
  • A \setminus B=\{x|x \in A và x \notin B\}.
  • Khi B \subset A thì A\setminus B được gọi là phần bù của B trong A. Kí hiệu C_A^B.

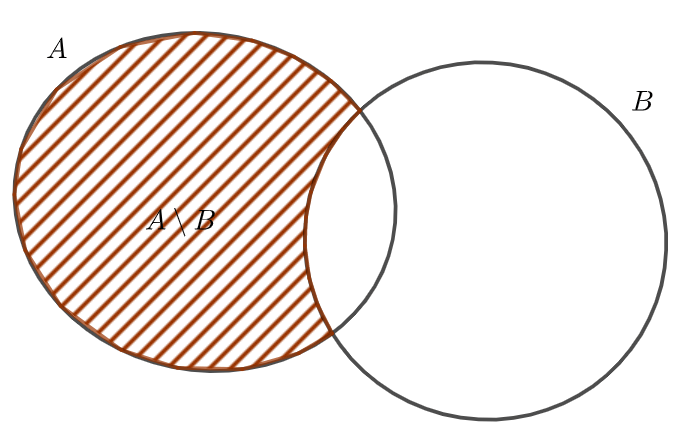
Biểu đồ Ven minh họa A\setminus B

Ví dụ 1: Cho tập A=\{0;1;2;3;4\} và tập B=\{2;3;4;5\}. Tìm tập hợp A\setminus B.

Hướng dẫn giải

Ta có: A \setminus B = \{0;1\}.

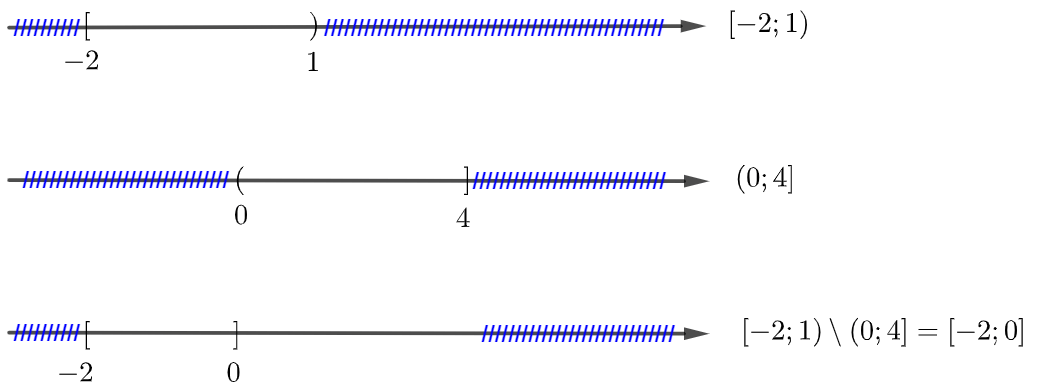
Ví dụ 2: Xác định tập hợp và biểu diễn trên trục số: [-2;1) \setminus (0;4].

Hướng dẫn giải

Ta có: [-2;1) \setminus (0;4] =[-2;0].

Biểu diễn trục số

 

 

 

 

  • 21 lượt xem

Toán 10 CD