Lớp 10 Toán 10 - Cánh diều

Hàm số và đồ thị

Bài học: Lí thuyết toán 10: Hàm số (Kết nối tri thức) đã giới thiệu cho các em về khái niệm hàm số, đồ thị hàm số và sự đồng biến nghịch biến của hàm số. Bên cạnh đó là một số ví dụ bài tập có lời giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình toán 10 Kết nối tri thức.

1. Hàm số. Tập xác định và giá trị của hàm số

Định nghĩa: Nếu với mỗi giá trị x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập hợp số thực R thì ta có một hàm số.

  • Ta gọi x là biến số, y là hàm số của x.
  • Tập hợp D được gọi là tập xác định của hàm số.
  • Tập hợp T gồm tất cả các giá trị y gọi là tập giá trị của hàm số.
  • Ta thường dùng kí hiệu f(x) để chỉ giá trị tương ứng với x, nên hàm số còn được viết là y=f(x).
  • Một hàm số có thể cho bằng bảng, biểu đồ, hoặc bằng công thức.

Ví dụ: 

  • Hàm số cho bởi bảng

Bảng dữ liệu thời tiết ngày 01/06/2020 tại thành phố Nha Trang.

Bảng trên biểu thị một hàm số, vì ứng với mỗi thời điểm (giờ) trong bảng thì đều có một giá trị báo nhiệt độ duy nhất.

Hàm số có tập xác định D=\{1;4;7;10;13;16;19;22\}.

Hàm số có tập giá trị T=\{27;28;29;31;32\}.

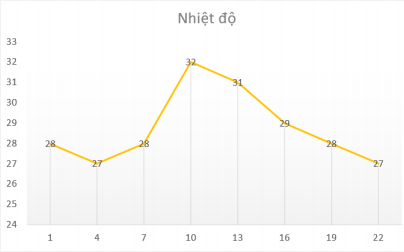
  • Hàm số cho bởi biểu đồ

Tương tự, biểu đồ "Dự báo nhiệt độ ngày 01/06/2020 tại thành phố Nha Trang" cũng là một hàm số, ta cũng có tập xác định và tập giá trị như ví dụ trên.

  • Hàm số cho bởi công thức

Ví dụ: y=2x-3 hay y=-x^2.

2. Đồ thị của hàm số

Đồ thị của hàm số y=f(x) xác định trên tập D là tập hợp tất cả các điểm M(x;f(x)) trên mặt phẳng tọa độ với mọi x thuộc D.

Chú ý: Điểm M(x_M;y_M) thuộc đồ thị hàm số  y=f(x) khi và chỉ khi x_M\in D và y_M=f(x_M).

Ví dụ: Đồ thị hàm số y=\dfrac{1}{2}x^2 đi qua điểm nào trong những điểm sau: A(1;1);B(\dfrac{1}{2};1)?

Giải:

Thay tọa độ điểm A vào công thức hàm số, ta được: 1\neq\dfrac{1}{2} .1 nên đồ thị hàm số không đi qua điểm A.

Thay tọa độ điểm B vào công thức hàm số, ta được: \frac12=1.\frac12 nên đồ thị hàm số đi qua điểm B .

3. Sự đồng biến, nghịch biến của hàm số

  • Hàm số f(x) được gọi là đồng biến (tăng) trên khoảng (a;b), nếu \forall x_1;x_2\in(a;b),x_1< x_2 \rightarrow f(x_1) < f(x_2).

Suy ra f(x) đồng biến trên (a;b) nếu: \forall x_1;x_2\in(a;b),x_1 \neq x_2 thì \frac{{f({x_2}) - f({x_1})}}{{{x_2} - {x_1}}} > 0.

  • Hàm số f(x) được gọi là nghịch biến (giảm) trên khoảng (a;b) , nếu \forall x_1;x_2\in(a;b),x_1< x_2 \rightarrow f(x_1) > f(x_2).

Suy ra f(x) nghịch biến trên (a;b) nếu: \forall x_1;x_2\in(a;b),x_1 \neq x_2 thì \frac{{f({x_2}) - f({x_1})}}{{{x_2} - {x_1}}} < 0.

Nhận xét

  • Nếu f (x) là hàm số đồng biến thì đồ thị đi lên (từ trái sáng phải).
  • Nếu f(x) là hàm số nghịch biến thì đồ thị đi xuống (từ trái sáng phải).
  • Nếu f(x) là hàm số hằng thì đồ thị là một đường thẳng song song / trùng với trục Ox.

Ví dụ 1: Khảo sát sự biến thiên của các hàm số sau:

  1. y=x+9 trên khoảng (0;+\infty)
  2. y=x^2-2 trên khoảng (-\infty;0)

Hướng dẫn giải

a. \forall x_1;x_2\in(0;+\infty ),x_1 \neq x_2 ta xét thương

\frac{{f({x_2}) - f({x_1})}}{{{x_2} - {x_1}}}= \frac{{({x_2} + 9) - ({x_1} + 9)}}{{{x_2} - {x_1}}} = 1 > 0.

Suy ra hàm số đồng biến trên khoảng (0;+\infty).

b. \forall x_1;x_2\in(-\infty;0 ),x_1 \neq x_2 ta xét thương

\frac{{f({x_2}) - f({x_1})}}{{{x_2} - {x_1}}} = \frac{{({x_2}^2 - 2) - ({x_1}^2 - 2)}}{{{x_2} - {x_1}}}= \frac{{{x_2}^2 - {x_1}^2}}{{{x_2} - {x_1}}} = {x_2} + {x_1} < 0.

Suy ra hàm số nghịch biến trên khoảng (-\infty;0).

Ví dụ 2: Tìm tập xác định của các hàm số sau:

  1. y=\frac{2x+3}{2x-1}
  2. y = \frac{{\sqrt { - 3x + 1} }}{{{x^2} + 2}}

Hướng dẫn giải

a. Điều kiện xác định:

2x - 1 \ne 0 \Leftrightarrow x \ne \frac{1}{2}.

Tập xác định của hàm số là D = \mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}.

b. Điều kiện xác định:

- 3x + 1 \ge 0 \Leftrightarrow x \le \frac{1}{3}.

Tập xác định của hàm số là D = \left[ {\frac{1}{3}; + \infty } \right).

Câu trắc nghiệm mã số: 7730,7731,7732,7733,7734
  • 11 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CD