Tam giác đều nội tiếp đường tròn bán kính 
cm có diện tích bằng:
Áp dụng định lí sin cho tam giác đều :
.
Diện tích tam giác :
.
Tam giác có . Diện tích của tam giác bằng:
Ta có: .
Diện tích tam giác: . (công thức Herong)
Tam giác có ,. Tính diện tích tam giác .
Diện tích tam giác: .
Tam giác cân có ,. Tính độ dài đường cao xuất phát từ đỉnh của tam giác.
Tam giác cân có 1 góc bằng
nên suy ra tam giác
đều.
Diện tích tam giác: .
Mặt khác: .
Hình bình hành có , và . Khi đó hình bình hành có diện tích bằng:
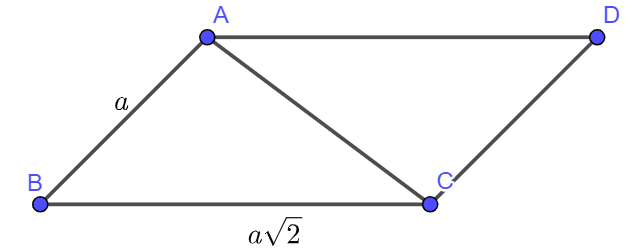
Ta có: .
Diện tích tam giác :
. Suy ra diện tích hình bình hành
.
Tam giác có . Tam giác có diện tích lớn nhất khi góc bằng:
Diện tích tam giác: mà
không đổi. Suy ra
khi
. Do đó
.
Cho tam giác có . Chọn khẳng định đúng:
Ta có: .
Diện tích tam giác: . (công thức Herong)
Tam giác cân có cạnh bên bằng và góc ở đỉnh bằng thì có diện tích là
Diện tích tam giác: .
Cho tam giác có ,. Chọn khẳng định đúng (kết quả làm tròn đến hàng phần chục)
Ta có: .
Áp dụng định lí sin:
Diện tích tam giác: .
Tam giác vuông tại có . Hai đường trung tuyến và cắt nhau tại . Diện tích tam giác bằng:
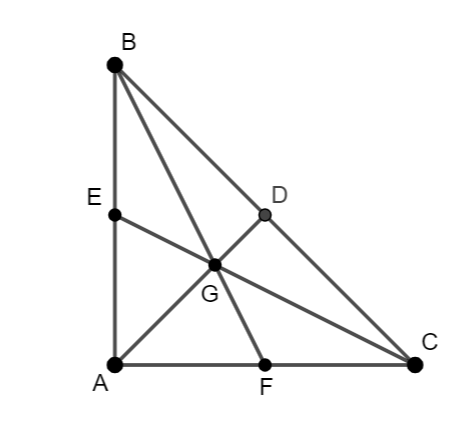
Gọi là trung điểm
. Suy ra
.
Tam giác vuông cân có cạnh bằng
. Suy ra
(cạnh huyền).
Vì là đường trung tuyến ứng với cạnh huyền nên
.
Ta có: .
Diện tích tam giác :
.
