Trắc nghiệm Toán 10 Chương 3 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

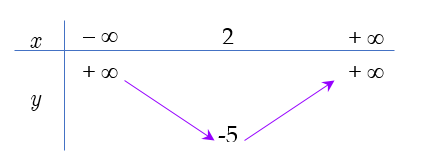
 Nhận xét: Từ bảng biến thiên ta suy ra đỉnh .

Chỉ có hàm số thỏa mãn tọa độ đỉnh này khi thay vào.

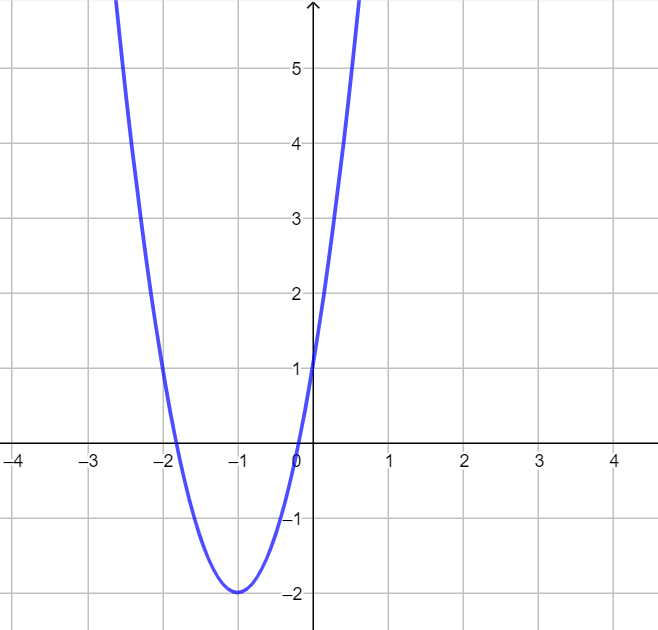
 Nhận xét: Từ hình vẽ suy ra đỉnh .

Thay tọa độ đỉnh vào các hàm số ở các đáp án, chỉ có hàm số thỏa mãn.

 Khi đồ thị hàm số hoàn toàn nằm phía trên trục hoành thì phương trình vô nghiệm Suy ra và (bề lõm hướng lên trên).

 Thay tọa độ và vào . Ta có:

.

Do đó .

Vì hàm số có trục đối xứng và đi qua điểm nên: 

và .

Nhận xét: Trong 4 đáp án, chỉ có thỏa mãn 2 điều kiện trên.

 Vì hàm số bậc hai có đỉnh nên:

và .

Suy ra .

 Nhận xét: Đồ thị hàm số bậc hai cắt trục hoành tại 2 điểm phân biệt nên suy ra phương trình có 2 nghiệm phân biệt. Suy ra .

Đỉnh nằm phía trên trục hoành nên suy ra (bề lõm hướng xuống). 

 Thay tọa độ và vào hàm số, ta được:

.

Vậy đó là hàm số .

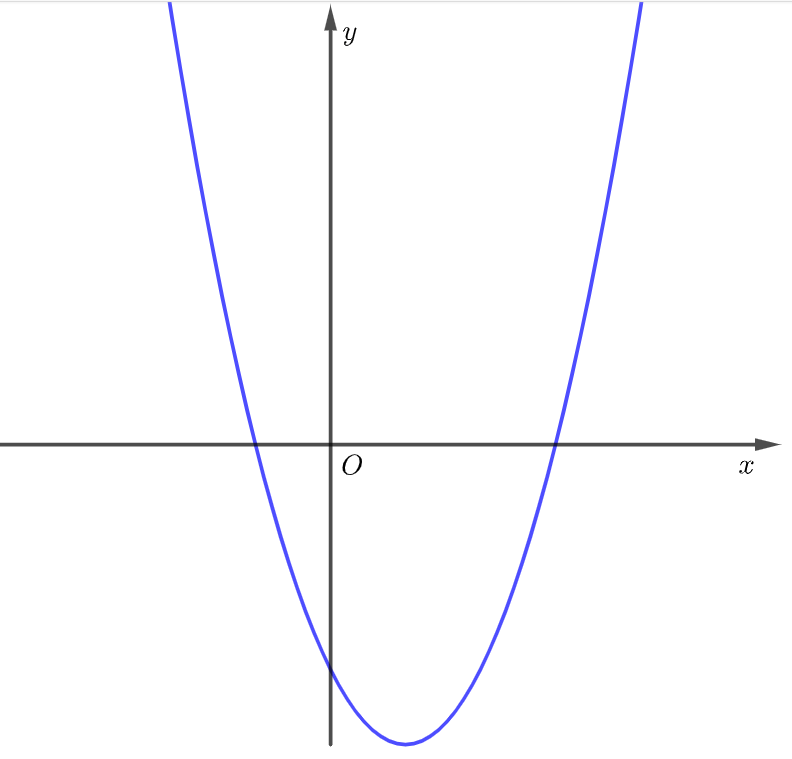
 Từ đồ thị hàm số, nhận xét:

Bề lõm hướng lên trên suy ra .

Hàm số cắt trục tung tại tung độ âm .

Chọn đáp án .