Khái niệm vectơ
1. Vectơ
- Là một đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu và điểm cuối.
- Kí hiệu: Nếu vectơ có điểm đầu là
 , điểm cuối là
, điểm cuối là  thì ta kí hiệu vectơ đó là
thì ta kí hiệu vectơ đó là  .
. - Đối với vectơ
 , ta gọi:
, ta gọi: - Đường thẳng đi qua hai điểm
 là giá của vectơ
là giá của vectơ  .
. - Độ dài đoạn thẳng
 là độ dài của vectơ
là độ dài của vectơ  , kí hiệu là
, kí hiệu là  .
. - Vectơ còn được kí hiệu là
 nếu không chỉ rõ điểm đầu điểm cuối.
nếu không chỉ rõ điểm đầu điểm cuối.
Ví dụ: Cho hình vuông ![]() tâm
tâm ![]() và có độ dài cạnh bằng
và có độ dài cạnh bằng ![]() . Tính độ dài các vectơ
. Tính độ dài các vectơ ![]() .
.
Hướng dẫn giải
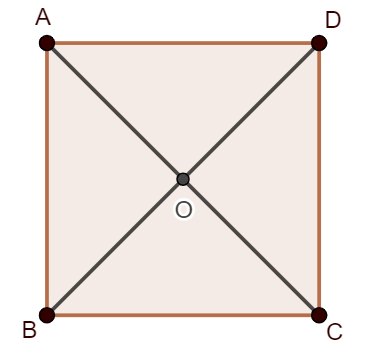
Vì cạnh của hình vuông bằng ![]() nên độ dài đường chéo bằng
nên độ dài đường chéo bằng ![]() . Do đó
. Do đó ![]() .
.
Vậy ![]() .
.
2. Phương và hướng của vectơ
- Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
- Hai vectơ cùng phương thì chúng hoặc là cùng hướng, hoặc là ngược hướng.
- Nhận xét: Ba điểm phân biệt
 thẳng hàng khi và chỉ khi hai vectơ
thẳng hàng khi và chỉ khi hai vectơ  cùng phương.
cùng phương.
Ví dụ: Hình vẽ bên mô tả hoạt động của ròng rọc khi dùng lực kéo một đầu. Chuyển động của các sợi dây tương ứng với các vectơ ![]() .
.
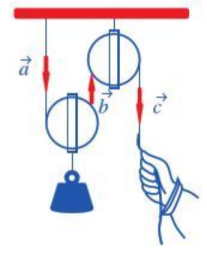
a) Hãy chỉ ra các vectơ cùng phương.
b) Hãy chỉ ra các vectơ cùng hướng, ngược hướng.
Hướng dẫn giải
a) Các vectơ ![]() có giá song song nên chúng cùng phương với nhau.
có giá song song nên chúng cùng phương với nhau.
b) Hai vectơ ![]() là hai vectơ cùng hướng. Hai vectơ
là hai vectơ cùng hướng. Hai vectơ ![]() là hai vectơ ngược hướng. Hai vectơ
là hai vectơ ngược hướng. Hai vectơ ![]() là hai vectơ ngược hướng.
là hai vectơ ngược hướng.
3. Hai vectơ bằng nhau, hai vectơ đối nhau
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng hướng và cùng độ dài, kí hiệu
 .
. - Hai vectơ được gọi là đối nhau nếu chúng ngược hướng và cùng độ dài, kí hiệu
 . Khi đó
. Khi đó  được gọi là vectơ đối của
được gọi là vectơ đối của  .
. - Cho vectơ
 và điểm
và điểm  , ta luôn tìm được một điểm
, ta luôn tìm được một điểm  duy nhất sao cho
duy nhất sao cho  . Khi đó độ dài của vectơ
. Khi đó độ dài của vectơ  là độ dài đoạn
là độ dài đoạn  , kí hiệu
, kí hiệu  .
. - Cho đoạn thẳng
 , ta luôn có:
, ta luôn có:  .
.
Ví dụ: Cho hình vuông ![]() có tâm
có tâm ![]() . Hãy chỉ ra bốn cặp vectơ bằng nhau, bốn cặp vectơ đối nhau.
. Hãy chỉ ra bốn cặp vectơ bằng nhau, bốn cặp vectơ đối nhau.
Hướng dẫn giải
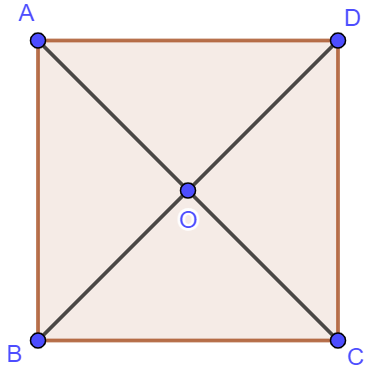
Bốn cặp vectơ bằng nhau là: ![]() và
và ![]() ;
; ![]() và
và ![]() ;
; ![]() và
và ![]() ;
; ![]() và
và ![]() .
.
Bốn cặp vectơ đối nhau là: ![]() và
và ![]() ;
; ![]() và
và ![]() ;
; ![]() và
và ![]() ;
; ![]() và
và ![]() .
.
4. Vectơ - không
Vectơ có điểm đầu và điểm cuối trùng nhau gọi là vectơ - không, kí hiệu ![]() . Ta có:
. Ta có:
 .
.- Vectơ - không luôn cùng phương, cùng hướng với mọi vectơ.
- Vectơ đối của vectơ - không là chính nó.
-
Chương 1: Mệnh đề toán học. Tập hợp
-
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
-
Chương 3: Hàm số và đồ thị
-
Chương 4: Hệ thức lượng trong tam giác. Vectơ
-
Đề thi học kì 1
-
Chương 5: Đại số tổ hợp
-
Đề thi giữa học kì 2
-
Chương 6: Một số yếu tố thống kê và xác suất
-
Chương 7: Phương pháp tọa độ trong mặt phẳng
-
Đề thi học kì 2







