Biến cố hợp, biến cố giao, biến cố độc lập Kết nối tri thức

Bộ tài liệu Lí thuyết Toán 11 Kết nối tri thức: Biến cố hợp, biến cố giao, biến cố độc lập bao gồm định nghĩa và cách xác định các dạng biến cố áp dụng tính xác suất. Ngoài ra có các bài tập ứng dụng có hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 11 KNTT giúp các em dễ dàng ôn tập củng cố.

1. Biến cố hợp

Hình vẽ minh họa

Ví dụ: Có hai chiếc hộp A B, mỗi hộp đựng 30 tấm thẻ, đánh số từ 1 đến 30. Từ mỗi hộp rút ngẫu nhiên một tấm thẻ. Kí hiệu a b, là số ghi trên thẻ tương ứng rút từ hộp A và hộp B.

Gọi M là biến cố: " a là số chẵn"; N là biến cố: "b là số chẵn".

Xét biến cố E: "  là số lẻ”.

Chứng minh rằng .

Hướng dẫn giải

Nếu xảy ra thì a là số chẵn, b là số lẻ, do đó a + b lẻ tức là E xảy ra.

Nếu xảy ra thì a là số lẻ, b là số chẵn, do đó a + b lẻ tức là E xảy ra.

Ngược lại, nếu E xảy ra thì a và b phải khác tính chẵn lẻ.

Nếu a chẵn, b lẻ thì xảy ra.

Nếu a lẻ, b chẵn thì xảy ra.

Vậy

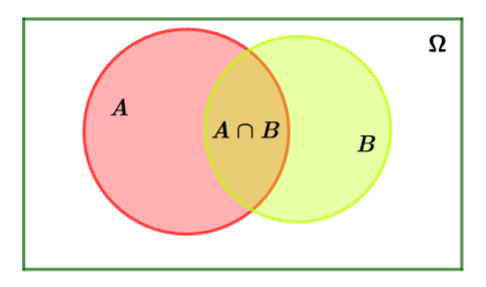
2. Biến cố giao

Hình vẽ minh họa

Ví dụ: Một hộp đựng 70 tấm thẻ, đánh số từ 1 đến 70. Rút ngẫu nhiên một tấm thẻ. Kí hiệu a là số ghi trên thẻ.

Gọi A là biến cố: "a là ước của 28", B là biến cố: "a là ước của 70". Xét biến cố

C: "a là ước của 14".

Chứng tỏ C là biến cố giao của A và B.

Hướng dẫn giải

Ta có:

Ta có:

Vậy C là biến cố giao của A và B.

3. Biến cố độc lập

Chú ý: Nếu cặp biến cố và độc lập thì các cặp biến cố cũng độc lập.

Ví dụ: Có hai lọ hoa. Lọ thứ nhất cắm 5 bông hoa hồng và 3 bông hoa cúc. Lọ thứ hai cắm 4 bông hoa hồng và 5 bông hoa thược dược. Lấy ngẫu nhiên đồng thời từ mỗi lọ một bông hoa. Xét hai biến cố sau:

A: "Lấy được bông hoa hồng từ lọ thứ nhất"

B: "Lấy bông hoa hồng từ lọ thứ hai".

Chứng minh rằng hai biến cố A, B độc lập.

Hướng dẫn giải

Dù A có xảy ra (lấy được bông hoa hồng) hay A không xảy ra (lấy được bông hoa cúc) ta đều có

Dù B có xảy ra (lấy được được bông hoa hồng) hay B không xảy ra (lấy được bông hoa thược dược) ta đều có

Việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia.

Vậy A và B độc lập.