Gọi ![]() là giao tuyến của mặt phẳng
là giao tuyến của mặt phẳng ![]() và
và ![]() . Nếu đường thẳng
. Nếu đường thẳng ![]() song song với cả hai mặt phẳng thì:
song song với cả hai mặt phẳng thì:
Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
Gọi ![]() là giao tuyến của mặt phẳng
là giao tuyến của mặt phẳng ![]() và
và ![]() . Nếu đường thẳng
. Nếu đường thẳng ![]() song song với cả hai mặt phẳng thì:
song song với cả hai mặt phẳng thì:
Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Khẳng định nào sau đây là đúng?
Hình vẽ minh họa
Ta có:
và d đi qua S
Cho ba mặt phẳng ![]() lần lượt giao nhau theo các giao tuyến phân biệt
lần lượt giao nhau theo các giao tuyến phân biệt ![]() . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng?
Theo định lí về giao tuyến của ba mặt phẳng thì đôi một song song hoặc đồng quy.
Cho hình chóp ![]() có đáy là hình thang có cạnh đáy là
có đáy là hình thang có cạnh đáy là ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() , điểm
, điểm ![]() . Xác định giao tuyến của hai mặt phẳng
. Xác định giao tuyến của hai mặt phẳng ![]() .
.
Hình vẽ minh họa
Ta có:
với
.
Vậy giao tuyến của hai mặt phẳng là đường thẳng qua P và song song với AB.
Cho hai đường thẳng song song a và b. Có bao nhiêu mặt phẳng chứa a và song song với b?
Tất cả những mặt phẳng chứa a và không chứa b đều là những mặt phẳng song song với b.
Cho hình hộp ![]() và điểm
và điểm ![]() nằm giữa
nằm giữa ![]() và
và ![]() . Giả sử
. Giả sử ![]() là mặt phẳng đi qua
là mặt phẳng đi qua ![]() và song song với mặt phẳng
và song song với mặt phẳng ![]() . Xác định các giao tuyến của mặt phẳng
. Xác định các giao tuyến của mặt phẳng ![]() tạo với các mặt của hình hộp. Hình xác định bởi các giao tuyến đó là hình gì?
tạo với các mặt của hình hộp. Hình xác định bởi các giao tuyến đó là hình gì?
Hình vẽ minh họa
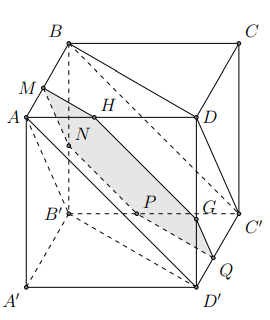
Nhận thấy
Do (1), ta giả sử (P) cắt BB’ tại N, suy ra , kết hợp với
suy ra
, suy ra N thuộc cạnh BB’.
Tương tự, giả sử suy ra
.
Kết hợp với (1) suy ra
Tương tự, sao cho
;
sao cho
;
sao cho
.
Từ đó suy ra thiết diện là lục giác .
Cho hình lập phương ![]() cạnh a. Gọi M là trung điểm của AB, N là tâm hình vuông
cạnh a. Gọi M là trung điểm của AB, N là tâm hình vuông ![]() . Xác định các giao tuyến của hình lập phương
. Xác định các giao tuyến của hình lập phương ![]() tạo với mặt phẳng
tạo với mặt phẳng ![]() . Tính diện tích hình tạo bởi các giao tuyến.
. Tính diện tích hình tạo bởi các giao tuyến.
Hình vẽ minh họa
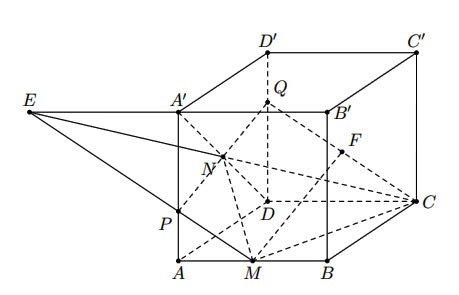
Hình tạo bởi các giao tuyến được biểu diễn như hình vẽ.
Tứ giác là hình thang có
Ta có:
với
Thay giá trị các cạnh ta có
Cho hình hộp ![]() . Tìm mặt phẳng song song với mặt phẳng
. Tìm mặt phẳng song song với mặt phẳng ![]() .
.
Hình vẽ minh họa
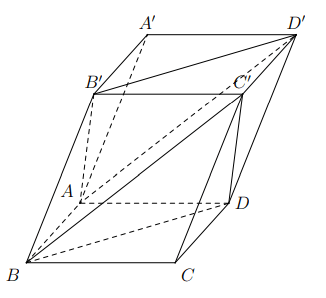
Ta có là hình bình hành nên
Tương tự ta có . Từ đó suy ra
và
.
Vậy
Cho hình chóp ![]() có đáy
có đáy ![]() là hình thang với đáy nhỏ
là hình thang với đáy nhỏ ![]() . Lấy các điểm
. Lấy các điểm ![]() sao cho
sao cho ![]() ,
, ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() . Để giao tuyến của mặt phẳng
. Để giao tuyến của mặt phẳng ![]() với các mặt của hình chóp
với các mặt của hình chóp ![]() là hình bình hành thì tỉ số độ dài cạnh
là hình bình hành thì tỉ số độ dài cạnh ![]() bằng:
bằng:
Hình biểu diễn
Ta có: với
và đi qua
, song song với
.
=> Giao tuyến của mặt phẳng với các mặt của hình chóp
là hình thang
. Tính
Để hình thang là hình bình hành thì
Cho hình chóp tứ giác ![]() , đáy
, đáy ![]() là tứ giác lồi. Gọi
là tứ giác lồi. Gọi ![]()
![]()
![]() . Xác định giao tuyến của hai mặt phẳng
. Xác định giao tuyến của hai mặt phẳng ![]() và
và ![]() ?
?
Hình vẽ minh họa
Nhận thấy S và M lần lượt là hai điểm chung của hai mặt phẳng (SAB) và (SCD).
Do đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là SM.
Cho ba mặt phẳng phân biệt cắt nhau từng đôi theo ba giao tuyến a, b, c, trong đó a song song với b. Khi đó vị trí tương đối của b và c là
Theo nội dung hệ quả của định lý về ba giao tuyến ta suy ra vị trí tương đối của b và c là song song.
Số cạnh của một hình chóp có đáy là một bát giác là:
Do đáy hình chóp là bát giác nên số cạnh đáy và số cạnh bên của hình chóp đều bằng 8.
Vậy hình chóp có 16 cạnh.
Cho tứ diện ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm
lần lượt là trung điểm ![]() và
và ![]() , G là trọng tâm tam giác BCD. Tìm giao tuyến d của hai mặt phẳng
, G là trọng tâm tam giác BCD. Tìm giao tuyến d của hai mặt phẳng ![]() và
và ![]() .
.
Hình vẽ minh họa
Hai mặt phẳng phân biệt (GMN) và (BCD) chứa hai đường thẳng song song MN và CD, đồng thời có điểm chung là G
=> Giao tuyến của chúng là đường thẳng d qua G và song song với CD (cắt BC, BD lần lượt tại P và Q).
Cho hình chóp tứ giác ![]() , đáy
, đáy ![]() là tứ giác (
là tứ giác (![]() không song song với
không song song với ![]() ),
), ![]() . Lấy
. Lấy ![]() là trung điểm của
là trung điểm của ![]() , lấy
, lấy ![]() sao cho
sao cho ![]() . Khi đó các cặp cạnh nào dưới đây cắt nhau?
. Khi đó các cặp cạnh nào dưới đây cắt nhau?
Hình vẽ minh hoạ
Các cặp đường thẳng SO và AD, MN và SC, SA và BC là các cặp đường thẳng chéo nhau.
Hai đường thẳng MN và SO nằm trên cùng mặt phẳng và là hai đường thẳng cắt nhau.
Trong không gian cho các đường thẳng a, b và các mặt phẳng (α), (β). Trong các khẳng định sau đây, đâu là khẳng định đúng?
Mệnh đề “a // (β) và (β) // b thì a // b” là sai vì a và b có thể cắt nhau.
Mệnh đề “a // b và b ⊂ (α) thì a // (α)” là sai vì có thể a ⊂ (α).
Mệnh đề “a // b và b // (α) thì a // (α)” là sai vì có thể a ⊂ (α).
