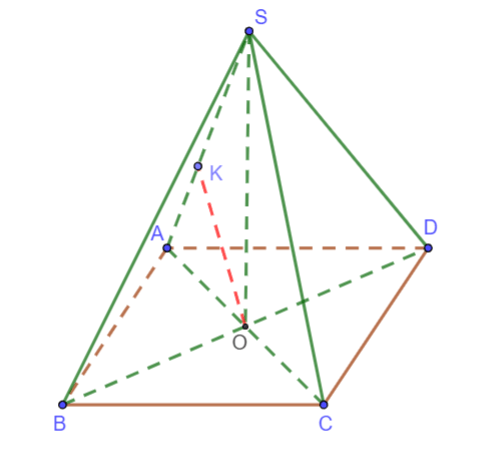
Cho tứ diện ABCD có AC = AD = BC = BD = a, (ACD) ⊥ (BCD) và (ABC) ⊥ (ABD). Tính độ dài cạnh CD.
Gọi M, N lần lượt là trung điểm của CD, AB, ∆ACD và ∆BCD cân
=> AM ⊥ CD, BM ⊥ CD. Ta có:
=> AM ⊥ BM
Và ta dễ dàng chứng minh được ∆ACD = ∆BCD (c – c - c)
=> AM = BM => ∆ABM vuông cân tại M
=> MN ⊥ AB
Đặt CD = x
Áp dụng định lý Py-ta-go ta có:
Xét ∆ABM vuông cân tại M
Áp dụng định lý Py-ta-go ta có:
Xét ∆CDN vuông cân tại N