Lớp 11 Toán 11 - Kết nối tri thức với cuộc sống

Luyện tập Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Nhận biết
    Chọn mệnh đề đúng?

    Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD). Mệnh đề nào sau đây là mệnh đề đúng?

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có: SA ⊥ (ABCD) nên tam giác SAB và tam giác SAD là tam giác vuông.

    Ta có: CD ⊥ DA mà DA là hình chiếu của DA trên (ABCD) nên CD vuông góc với DS

    => Mặt bên SDC là tam giác vuông tại D

    Tương tự ta có: mặt bên SBC là tam giác vuông tại B. Như vậy chỉ có khẳng định ”Mặt bên của hình chóp là những tam giác vuông” là chắc chắn đúng.

  • Câu 2: Vận dụng cao
    Tính sin γ

    Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và \widehat{ABC} = 60^{0}, SB = a. Hình chiếu vuông góc của điểm S lên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Gọi γ là góc giữa đường thẳng SB và mặt phẳng (SCD). Tính sinγ.

    Hướng dẫn:

    Hình vẽ minh họa:

    Gọi M là trung điểm của SD

    Góc giữa SB và (SCD) cùng bằng góc giữa OM và (SCD)

    (Vì OM // SB)

    Gọi H là hình chiếu của O trên (SCD) => (OM; (SCD)) = (OM; MH) = OMH

    Trong (SBD) kẻ OE // SK, trong đó K là hình chiếu của S lên mặt đáy, khi đó tứ diện OECD là tứ diện vuông cân nên

    \begin{matrix}\dfrac{1}{OH^{2}} = \dfrac{1}{OC^{2}} + \dfrac{1}{OD^{2}} +\dfrac{1}{OE^{2}}\hfill \\OC = \dfrac{a}{2},OD = \dfrac{a\sqrt{3}}{2}\hfill \\\dfrac{OE}{SK} = \dfrac{OD}{KD} = \dfrac{3}{4} \Rightarrow OE =\dfrac{3}{4}SK\hfill \\\Rightarrow SK = \sqrt{SB^{2} - BK^{2}} = \sqrt{a^{2} - \left(\dfrac{a\sqrt{3}}{3} ight)^{2}} = \dfrac{a\sqrt{6}}{3} \hfill\\\Rightarrow OE = \dfrac{3}{4}SK = \dfrac{3}{4} \cdot \dfrac{a\sqrt{6}}{3} =\dfrac{a\sqrt{6}}{4}\hfill \\\Rightarrow \dfrac{1}{OH^{2}} = \dfrac{1}{\left( \dfrac{a}{2} ight)^{2}}+ \dfrac{1}{\left( \dfrac{a\sqrt{3}}{2} ight)^{2}} + \dfrac{1}{\left(\dfrac{a\sqrt{6}}{4} ight)^{2}} = \dfrac{a^{2}}{8}\hfill \\\Rightarrow OH = \dfrac{a\sqrt{2}}{4}\hfill \\\end{matrix}

    Vì tam giác AOM vuông tại H

    \begin{matrix}\Rightarrow OM = \dfrac{1}{2}SB = \dfrac{a}{2},OH = \dfrac{a\sqrt{2}}{4}\hfill \hfill\\\Rightarrow \sin\widehat{OMH} = \dfrac{OH}{OM} = \dfrac{\sqrt{2}}{2}\Rightarrow \sin\varphi = \dfrac{\sqrt{2}}{2}\hfill \\\end{matrix}

  • Câu 3: Nhận biết
    Mệnh đề nào sau đây là mệnh đề đúng?

    Cho tam giác ABC vuông tại A và có hai đỉnh B và C nằm trên mặt phẳng (P). Gọi C’ là hình chiếu vuông góc của đỉnh C lên mặt phẳng (P). Trong các mệnh đề sau mệnh đề nào đúng?

    Hướng dẫn:

    Vì C’ trùng với C nên tam giác ABC’ là tam giác vuông tại A.

  • Câu 4: Nhận biết
    Chọn khẳng định đúng?

    Cho tam giác ABC vuông tại A và có hai đỉnh B và C nằm trên mặt phẳng (P). Gọi A’ là hình chiếu vuông góc của đỉnh A lên mặt phẳng (P). Trong các mệnh đề sau mệnh đề nào đúng?

    Hướng dẫn:

    \begin{matrix} \overrightarrow{A'B}.\overrightarrow{A'C} = \overrightarrow{A'A}.\overrightarrow{A'C} + \overrightarrow{AB}.\overrightarrow{A'C} \\ = \overrightarrow{AB}.\overrightarrow{A'C} = \overrightarrow{AB}.\left( \overrightarrow{A'A} + \overrightarrow{AC} ight) \\ = \overrightarrow{AB}.\overrightarrow{A'A} = - \overrightarrow{AB}.\overrightarrow{AA'} < 0 \\ \end{matrix}

    => Góc BA’C là góc tù.

  • Câu 5: Thông hiểu
    Hoàn thành mệnh đề

    Cho hình chóp S.ABC có đáy ABC là tam giác nhọn, SA = SB = SC. Gọi I là hình chiếu vuông góc của S trên mặt phẳng đáy. Khi đó:

    Hướng dẫn:

    Hình vẽ minh họa:

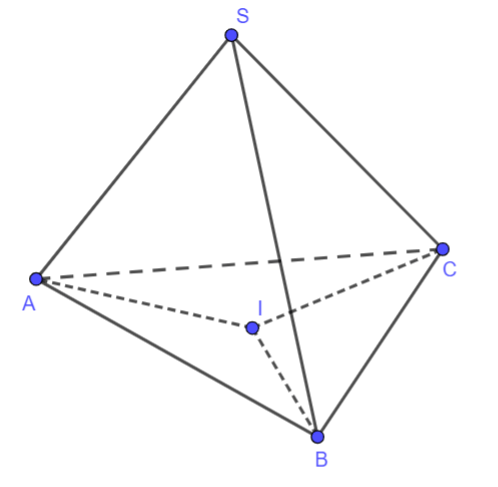
    Hoàn thành mệnh đề

    Ta có I là hình chiếu vuông góc của S trên mặt phẳng (ABC)

    Tam giác SAI vuông tại I

    => SA2 = AI2 + SI2

    Tam giác SBI vuông tại I

    => SB2 = BI2 + SI2

    Tam giác SCI vuông tại I

    => SC2 = CI2 + SI2

    Kết hợp với điều kiện: SA = SB = SC

    => I là tâm đường tròn ngoại tiếp tam giác ABC.

  • Câu 6: Thông hiểu
    Chọn khẳng định đúng

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC). Gọi I là tâm đường tròn ngoại tiếp tam giác SBC, H là hình chiếu của I trên mặt phẳng đáy. Chọn khẳng định đúng trong các khẳng định dưới đây?

    Hướng dẫn:

    Hình vẽ minh họa:

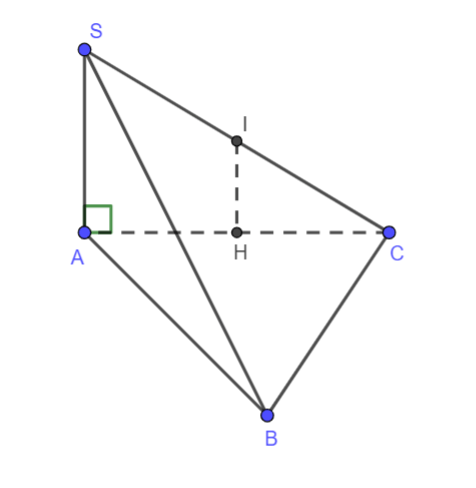
    Chọn khẳng định đúng

    Ta có: SA ⊥ (ABC) => SA ⊥ BC

    Mà AB ⊥ BC => BC ⊥ (SAB) => BC ⊥ SB

    => Tam giác SBC vuông tại B => I là trung điểm của SC

    Theo bài ra ta có: IH ⊥ (ABC) => IH // SA

    => H là trung điểm của cạnh AC,

    Mà tam giác ABC vuông tại B => H là tâm đường tròn ngoại tiếp tam giác ABC.

  • Câu 7: Thông hiểu
    Hoàn thành mệnh đề

    Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Nếu H là hình chiếu vuông góc của điểm O trên mặt phẳng (ABC) thì H là:

    Hướng dẫn:

    Vì \left\{ \begin{matrix} AB\bot OH \\ AB\bot OC \\ \end{matrix} ight.\ \Rightarrow AB\bot CH

    Tương tự: BC\bot AH

    Vậy H là trực tâm tam giác ABC.

  • Câu 8: Nhận biết
    Chọn khẳng định sai?

    Cho hình lập phương ABCD.A1B1C1D1. Chọn khẳng định sai?

    Hướng dẫn:

    Hình vẽ minh họa:

    Dễ thấy

    Góc giữa B1D1 và AC bằng 900

    Góc giữa AD và C1B bằng 450

    Góc giữa BD và CA1 bằng 900

    Đều là các đáp án đúng

    Góc giữa B1D1 và AA1 bằng 600 sai vì \widehat{\left( B_{1}D_{1};AA_{1} ight)} = 90^{0}

  • Câu 9: Vận dụng cao
    Diện tích thiết diện

    Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh a, tâm O, đường cao AA’, SO = 2a. Gọi M là điểm thuộc đoạn OA’ (M khác O và A’). Mặt phẳng (α) đi qua M và vuông góc với AA’. Đặt MA = x. Tính diện tích S thiết diện tạo bởi mặt phẳng (α) và hình chóp.

    Hướng dẫn:

    Hình vẽ minh họa:

    Vì S.ABC là hình chóp đều => SO⊥(ABC) (với O là tâm của tam giác ABC)

    Do đó: SO ⊥ AA’ mà (α) ⊥ AA’ => SO // (α)

    Tương tự ta cũng có BC // (α)

    Qua M kẻ IJ // BC (I thuộc AB, J thuộc AC), kẻ MN // SO với N thuộc SA’

    Qua N kẻ EF // BC với E thuộc SB và F thuộc SC

    Khi đó thiết diện là hình thang IJEF

    Diện tích hình thang là:

    S_{IJEF} = \frac{1}{2}(IJ + EF).MN

    Xét tam giác ABC ta có:

    \frac{IJ}{BC} = \frac{AM}{AA'} \Rightarrow IJ = \frac{AM.BC}{AA'} = \frac{2x\sqrt{3}}{3}

    Xét tam giác SBC ta có:

    \frac{EF}{BC} = \frac{SN}{SA'} = \frac{OM}{OA'} \Rightarrow EF = \frac{OM.BC}{OA'} = 2\left( x\sqrt{3} - a ight)

    Xét tam giác SOA’ có:

    \frac{MN}{SO} = \frac{MA'}{OA'} \Rightarrow MN = \frac{OS.MA'}{OA'} = 2\left( 3a - 2x\sqrt{3} ight)

    \begin{matrix}S_{IJEF} = \dfrac{1}{2}(IJ + EF).MN \hfill \\= \dfrac{2}{3}\left( 4x\sqrt{3} - 3a ight)\left( 3a - 2x\sqrt{3}ight) \hfill\\= - 2\left( 8x^{2} - 6\sqrt{3}x + 3a^{2} ight) \hfill\\\end{matrix}

  • Câu 10: Thông hiểu
    Xác định góc giữa đường thẳng và mặt phẳng

    Cho hình chóp S.ABC có SA ⊥(ABC). Biết α là góc giữa SB và mặt phẳng (ABC). Xác định góc α.

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có SA ⊥(ABC) => Hình chiếu của SB trên mặt phẳng (ABC) là đường thẳng AB.

    => Góc giữa đường thẳng SB và (ABC) là góc giữa hai đường thẳng SB và AB

    Tức là \alpha = \widehat{SBA}

  • Câu 11: Vận dụng
    Tính góc giữa đường thẳng và mặt phẳng

    Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA = a\sqrt{2}, SA ⊥ (ABCD). Tính góc giữa đường thẳng SC và mặt phẳng (SAD).

    Hướng dẫn:

    Hình vẽ minh họa:

    Gọi M là trung điểm của AD

    => ABCM là hình vuông => CM ⊥ AD

    Ta có: \left\{ \begin{matrix} CM\bot AC \\ CM\bot SA \\ \end{matrix} ight.\ \Rightarrow CM\bot(SAD)

    Suy ra hình chiếu vuông góc của SC trên mặt phẳng (SAD) là SM

    \Rightarrow \left( SC;(SAD) ight) = (SC;SM) = \widehat{CSM}

    => \tan\widehat{CSM} = \frac{CM}{SM} = \frac{AB}{\sqrt{SA^{2} + AM^{2}}} = \frac{1}{\sqrt{3}}

    => \widehat{CSM} = 30^{0}

  • Câu 12: Thông hiểu
    Chọn đáp án đúng

    Cho hình chóp S.ABC có các mặt bên tạo với đáy một góc bằng nhau. Hình chiếu vuông góc của điểm S trên mặt phẳng (ABC) là:

    Hướng dẫn:

    Gọi I là hình chiếu vuông góc của S trên mặt phẳng (ABCD)

    M, N, P lần lượt là hình chiếu vuông góc của S trên các cạnh AB, AC, BC.

    Khi đó ta có: \left\{ \begin{matrix}SI\bot AB \\SM\bot AB \\\end{matrix} ight.\ \Rightarrow AB\bot(SIM) \Rightarrow AB\botIM

    Tương tự ta có: AC\bot IN,IP\botBC

    Khi đó \left( (SAB);(ABC) ight) =(SM,IM) = \widehat{SMI}

    Tương tự suy ra \widehat{SMI} =\widehat{SNI} = \widehat{SPI}

    => \Delta SMI = \Delta SNI = \DeltaSPI \Rightarrow IM = IN = IP

    => I là tâm đường tròn nội tiếp tam giác ABC.

  • Câu 13: Thông hiểu
    Kết luận nào sau đây đúng?

    Trong mặt phẳng (P) cho tam giác ABC, M là điểm không nằm trên (P) sao cho MA = MB = MC, d là đường thẳng đi qua M và vuông góc với (P). Khi đó đường thẳng d đi qua:

    Hướng dẫn:

    Gọi H là giao điểm của đường thẳng d và mặt phẳng (P)

    => H là hình chiếu của M trên (P) nên từ MA = MB = MC

    => HA = HB = HC

    => Khi đó đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC.

  • Câu 14: Vận dụng
    Tính góc giữa cạnh bên và mặt đáy

    Cho lăng trụ ABCD.A’B’C’D’ có đáy là hình thoi cạnh a, \widehat{BAD} = 60^{0}. Hình chiếu vuông góc của B’ xuống mặt đáy trùng với giao điểm hai đường chéo của đáy và cạnh bên BB’ = a. Tính góc giữa cạnh bên và mặt đáy.

    Hướng dẫn:

    Hình vẽ minh họa:

    Gọi O là giao điểm của AC và BD

    Theo giả thiết ta có: B’O ⊥ (ABCD)

    Dó đó \left( BB';(ABCD) ight) = (BB';BO) = \widehat{B'BO}

    Vì tam giác ABD đều cạnh a => BO = \frac{BD}{2} = \frac{a}{2}

    Tam giác B’BO vuông ta có:

    \begin{matrix}\cos\widehat{B'BO} = \dfrac{BO}{BB'} = \dfrac{1}{2} \hfill \\\Rightarrow \widehat{B'BO} = 60^{0} \hfill \\\end{matrix}

  • Câu 15: Vận dụng
    Chọn khẳng định đúng

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm của AB, AD. Gọi α là góc giữa SA và (SHK). Chọn mệnh đề đúng?

    Hướng dẫn:

    Hình vẽ minh họa:

    Gọi I là giao điểm của HK và AC

    Dễ dàng suy ra HK // BD => HK ⊥ AC

    Ta lại có: AC ⊥ SH

    => AC ⊥ (SHK)

    => \left( SA;(SHK) ight) = (SA;SI) = \widehat{ASI}

    Tam giác SIA vuông tại I ta có:

    \tan\widehat{ASI} = \dfrac{AI}{SI} =\dfrac{\dfrac{1}{4}AC}{\sqrt{SA^{2} - AI^{2}}} =\dfrac{\sqrt{7}}{7}

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (27%):
    2/3
  • Thông hiểu (40%):
    2/3
  • Vận dụng (20%):
    2/3
  • Vận dụng cao (13%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 3 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 KNTT

Đăng nhập