Cho a, b, c là các đường thẳng trong không gian. Mệnh đề nào dưới đây sai?
Nếu a ⊥ b, b ⊥ c thì a // c hoặc a cắt c hoặc a trùng với c hoặc a chéo c.
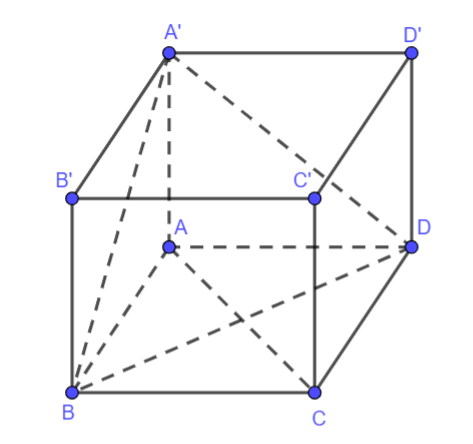
Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc với nhau. Điểm nào cách đều bốn đỉnh của A, B, C, D của tứ diện ABCD?
Hình vẽ minh họa:
Ta có:
=> Tam giác ABD vuông tại B.
=> IA = IB = ID = AD/2 (với I là trung điểm của AD)
Ta có:
=> Tam giác BCD vuông tại C.
=> EA = EC = ED = AD/2 (E là trung điểm của AD)
Vậy I trùng với E
Vậy điểm cách đều bốn đỉnh của A, B, C, D của tứ diện ABCD là trung điểm của đoạn thẳng AD.
Cho hình chóp S.ABCD có SA ⊥ (ABCD) có đáy ABCD là hình thoi tâm O. Mệnh đề nào sai?
Hình vẽ minh họa:
Ta có: SA ⊥ (ABCD) => SA vuông góc với BD.
Do tứ giác ABCD là hình thoi nên BD vuông góc với AC mà SA⊥BD => BD ⊥ (SAC)
=> BD ⊥ SC, BD ⊥ SO
Dễ thấy AD không vuông góc với SC vì nếu AD vuông góc với SC thì AD ⊥ AC vô lí
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy. Trực tâm của tam giác SBC và ABC lần lượt là H và K. Khẳng định nào dưới đây là khẳng định sai?
Ta có: BC ⊥ SA, BC ⊥ SH => BC ⊥ (SAH)
CK ⊥ AB, CK ⊥ SA => CK ⊥ (SAB) => CK ⊥ SB
Mặt khác CH ⊥ SB => SB ⊥ (CHK)
Ta có: BC ⊥ (SAH) => BC ⊥ HK
SB ⊥ (CHK) => SB ⊥ HK
=> HK ⊥ (SBC)
Dùng phương pháp loại trừ ta suy ra: BC ⊥ (SAB) là đáp án sai.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ⊥ (ABCD). Gọi AM, AN lần lượt là đường cao của tam giác SAB và tam giác SAD. Khẳng định nào dưới đây là khẳng định đúng?
Hình vẽ minh họa:
Ta có: SA ⊥ (ABCD) => SA ⊥ BC
Mà AB ⊥ BC => BC ⊥ (SAB)
=> BC ⊥ AE
Mà AM nằm trong mặt phẳng (SAB)
Xét tam giác SAB có:
AM ⊥ SB
Mà BC ⊥ AM => AM ⊥ (SBC) => AM ⊥ SC
Chứng minh tương tự ta được: AN ⊥ SC
=> SC ⊥ (AMN)
Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc với nhau và AB = a, BC = b, CD = c. Độ dài đoạn thẳng AD bằng bao nhiêu?
Hình vẽ minh họa:
Ta có:
=> Tam giác ABD vuông tại B.
Ta có:
=> Tam giác BCD vuông tại C.
Ta có:
Trong không gian cho đường thẳng a và điểm M. Có bao nhiêu đường thẳng đi qua M và vuông góc với a?
Trong không gian cho đường thẳng a và điểm M. Gọi (P) là mặt phẳng đi qua M vuông góc với a. Khi đó mọi đường thẳng nằm trong mặt phẳng (P) và đi qua M đều vuông góc với a.
=> Vậy có vô số đường thẳng đi qua M và vuông góc với a.
Cho hình chóp S.ABCD có ABCD là hình thoi tâm O, SA = SC; SB = SD. Khẳng định nào dưới đây là khẳng định sai?
Hình vẽ minh họa:
Ta có: Tam giác SAC và tam giác SBD lần lượt là tam giác cân tại S
=> SO ⊥ AC, SO ⊥ BD
=> SO ⊥ (ABCD)
Dễ thấy:
SO ⊥ (ABCD)
AC ⊥ BD
BD ⊥ (SAC)
Là những khẳng định đúng.
Cho hình chóp đều S.ABC có cạnh đáy bằng x, cạnh bên bằng y. Mặt phẳng (α) đi qua A và vuông góc với SC. Tìm hệ thức liên hệ giữa x và y để (α) cắt SC tại điểm C1 nằm giữa S và C.
Hình vẽ minh họa:
Gọi G là trọng tâm của tam giác ABC
Do S.ABC là hình chóp đều nên SG ⊥ (ABC). Gọi C’ là trung điểm của AB
=> C, C’, G thẳng hàng
Ta có:
Trong tam giác SAC kẻ AC1⊥SC
=> SC ⊥ (ABC1)
=> Thiết diện cần tìm là tam giác ABC1 thỏa mãn đi qua A và vuông góc với SC. Tam giác SAC cân tại S nên để C1 nằm giữa S và C khi và chỉ khi .
Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1. Gọi (P) là mặt phẳng chứa CD’ và tạo với mặt phẳng BDD’B’ một góc x nhỏ nhất, cắt hình lập phương theo một thiết diện có diện tích S. Giá trị của S bằng:
Hình vẽ minh họa:
Góc của (P) qua CD’ hợp với (BB’D’D) một góc nhỏ nhất bằng với góc giữa đường thẳng CD’ và (BB’D’D).
Ta có:
=> D là trung điểm của BM.
Kéo dài MD’ cắt BB’ tại N. Đường thẳng CN cắt B’C’ tại I, ta được I là trung điểm B’C’.
Ta được thiết diện cần tìm là tam giác ICD’
Tính được:
Khẳng định nào sau đây là sai?
Mệnh đề sai là: “Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong (α) thì d ⊥ (α).”
Vì thiếu điều kiện “cắt nhau” của hai đường thẳng nằm trong (α).
Ví dụ đường thẳng a vuông góc với hai đường thẳng b và c nằm trong (α) nhưng b và c song song với nhau thì khi đó a chưa chắc vuông góc với (α).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC), H là chân đường cao kẻ từ A của tam giác SAB. Khẳng định nào dưới đây là khẳng định sai?
Hình vẽ minh họa:
Ta có: SA ⊥ (ABC) mà BC thuộc (ABC)
=> SA ⊥ BC
Xét tam giác ABC vuông tại B ta có:
AB ⊥ BC
=> BC ⊥ (SAB) => BC ⊥ AH
Khi đó: AH ⊥ SB, AH ⊥ BC => AH ⊥ (SBC) => AH ⊥ SC
Nếu có: AH ⊥ AC trong khi SA ⊥ AC thì AC ⊥ (SAB)
=> AC ⊥ AB (vô lí)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, SA ⊥ (ABCD), AD = CD = a, AB = 2a. Gọi E là trung điểm của AB. Chỉ ra mệnh đề sai trong các mệnh đề dưới đây.
Từ giả thiết suy ra ADCE là hình vuông
=> CE ⊥ AB, CE = AD = a
Ta có: CE ⊥ AB, CE ⊥ SA => CE ⊥ (SAB)
Vì CE = AD = a =>
=> Tam giác ABC vuông tại C => CB ⊥ AB
Kết hợp với CB ⊥ SA => CB ⊥ (SAC)
Ta có:
CD ⊥ AD, CD ⊥ SA => CD ⊥ (SAD)
=> Tam giác SDC vuông tại D
Dùng phương pháp loại trừ nên ta có: CE ⊥ (SDC) là khẳng định sai.
Cho hình lập phương ABCD.A’B’C’D’. Đường thẳng AC’ vuông góc với mặt phẳng nào sau đây?
Hình vẽ minh họa:
Ta có: AA’D’A là hình vuông => AD’ ⊥ A’D
ABCD.A’B’C’D là hình lập phương => AB ⊥ A’D
=> A’D ⊥ (ABC’D’) => A’D ⊥ AC’
Ta lại có: ABCD là hình vuông => AC ⊥ BD
Mà A’A ⊥ BD => BD ⊥ (AA’C’C) => BD ⊥ AC’
Kết hợp với A’D ⊥ AC’ => A’C ⊥ (A’BD)
Trong các mệnh đề sau, mệnh đề nào đúng?
Mệnh đề: “Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng và đường thẳng b với b vuông góc với (P).” sai vì hai góc này phụ nhau.
Mệnh đề: “Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng a và mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q).” sai vì (P) có thể trùng với (Q).
Mệnh đề: “Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) thì a song song với b.” sai vì a có thể trùng với b.
