Lớp 11 Toán 11 - Kết nối tri thức với cuộc sống

Giá trị lượng giác của góc lượng giác KNTT

Bộ tài liệu Lí thuyết Toán 11 Kết nối tri thức: Giá trị lượng giác của góc lượng giác bao gồm định nghĩa, tính chất và các công thức lượng giác và các bài tập ứng dụng có hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 11 KNTT giúp các em dễ dàng ôn tập củng cố.

1. Góc lượng giác

a) Khái niệm góc lượng giác và số đo của góc lượng giác

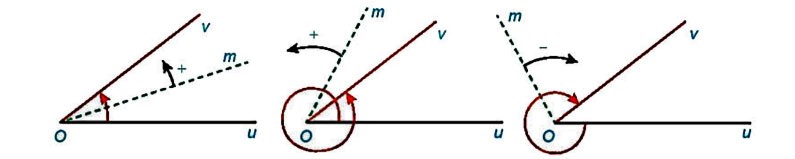
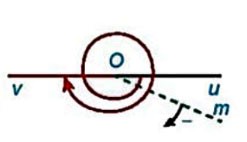
Trong mặt phẳng cho hai tia Ou,Ov. Xét tia Om cùng nằm trong mặt phẳng này. Nếu tia Om Om quay quanh điểm O, theo một chiều nhất định từ O đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou, tia cuối Ov và kí hiệu là \left( {Ou,Ov} \right).

Ta quy ước: Chiều quay ngược với chiều quay của kim đồng hồ là chiều dương, chiều quay cùng chiều kim đồng hồ là chiều âm.

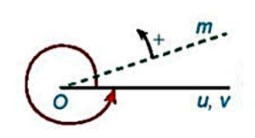
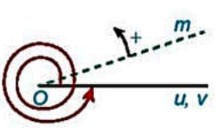
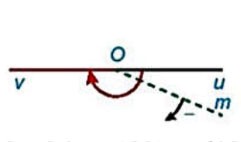
Giá trị lượng giác của góc lượng giác KNTT

Khi đó tia Om quay theo chiều dương đúng nửa vòng ta nói tia Om quay góc {180^0}, quay đúng 1 vòng ta nói nó quay được góc {360^0}; quay theo chiều âm 1 vòng ta nói nó quay góc - {360^0}; quay theo chiều âm hai vòng ta nói nó quay được góc - {2.360^0} = - {720^0}; …

Khi tia Om quay được một góc {\alpha ^0} ta nói góc lượng giác mà tia đó quét nên có số đo là {\alpha ^0}. Số đo của góc lượng giác có tia đầu Ou, tia cuối Ov được kí hiệu là sd\left( {Ou,Ov} \right)

Giá trị lượng giác của góc lượng giác KNTT sd\left( {Ou,Ov} \right) = {360^0}
Giá trị lượng giác của góc lượng giác KNTT sd\left( {Ou,Ov} \right) = {720^0}
Giá trị lượng giác của góc lượng giác KNTT sd\left( {Ou,Ov} \right) = - {180^0}
Giá trị lượng giác của góc lượng giác KNTT sd\left( {Ou,Ov} \right) = - {540^0}

Chú ý: Cho hai tia Ou,Ov thì có vô số góc lượng giác tia đầu Ou và tia cuối Ov. Số đo của các góc lượng giác này khác nhau một bội số nguyên của {360^0}.

Ví dụ: Cho góc hình học AOM có số đo {45^0}. Xác định số đo góc của các góc lượng giác \left( {OA,OM} \right) và \left( {OM,OA} \right)?

Hướng dẫn giải

Hình vẽ minh họa

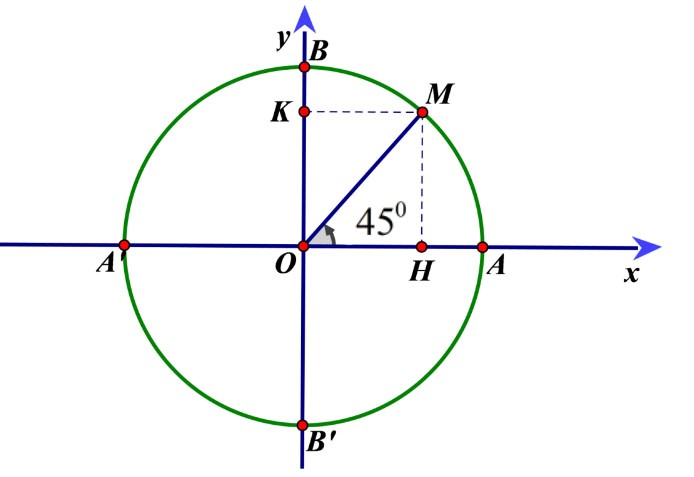
Giá trị lượng giác của góc lượng giác KNTT

Ta có:

Các góc lượng giác có tia đầu OA, tia cuối OM có số đo là

sd\left( {OA,OM} \right) = {45^0} + k{.360^0};\left( {k \in \mathbb{Z}} \right)

Các góc lượng giác có tia đầu OM, tia cuối OA có số đo là

sd\left( {OM,OA} \right) = - {45^0} + k{.360^0};\left( {k \in \mathbb{Z}} \right)

b) Hệ thức Chasles

Hệ thức Chasles: Với ba tia bất kì Ou,Ov,Ow, ta có:

sd\left( {Ou,Ov} \right) + sd\left( {Ov,Ow} \right) = sd\left( {Ou,Ow} \right) + k{.360^0};\left( {k \in \mathbb{Z}} \right)

2. Đơn vị đo góc và đo độ dài cung tròn

a) Đơn vị đo góc và cung tròn

Đơn vị độ: Để đo góc, ta dùng đơn vị độ. Ta đã biết: Góc bằng \frac{1}{{180}} góc bẹt.

Đơn vị radian: Cho đường tròn \left( O \right) tâm O, bán kính R và một cung AB .

Ta nói cung tròn AB có số đo bằng 1 radian nếu độ dài của nó đùng bằng bán kính R.

Khi đó ta cũng nói góc  có số đo bằng 1 radian và viết: \widehat {AOB} = 1rad

Quan hệ giữa độ và radian

{1^0} = \frac{\pi }{{180}};1rad = {\left( {\frac{{180}}{\pi }} \right)^0}

Ví dụ: a) Đổi từ độ sang radian các số đo: {360^0}; - {450^0}

b) Đổi từ radian sang độ các số đo sau: 3\pi ;\frac{{ - 11\pi }}{5}

Hướng dẫn giải

a) Đổi từ độ sang radian các số đo:

{360^0} = 360.\frac{\pi }{{180}} = 2\pi

- {450^0} = - 450.\frac{\pi }{{180}} = - \frac{\pi }{4}

b) Đổi từ radian sang độ các số đo sau:

3\pi = 3\pi .{\left( {\frac{{180}}{\pi }} \right)^0} = {540^0}

\frac{{ - 11\pi }}{5} = \frac{{ - 11\pi }}{5}.{\left( {\frac{{180}}{\pi }} \right)^0} = - {396^0}

b) Độ dài cung tròn

Một cung của đường tròn bán kính R và có số đo  thì có độ dài là: 

l = R.\alpha

Ví dụ: Bánh xe của người đi xe đáp quay được 12 vòng trong 6 giây.

a) Tính góc (theo độ và radian) mà bánh xe quay được trong 1 giây.

b) Tính độ dài quãng đường mà người đi xe đạp đã đi được trong 1 phút, biết rằng đường kính của bánh xe đạp là 600mm.

Hướng dẫn giải

a) 1 giây bánh xe quay được: \frac{{12}}{6} = 2 vòng

Góc mà bánh xe quay được trong giây là {2.360^0} = {720^0} = 4\pi \left( {rad} \right)

b) Ta có: 1 phút = 60 giây 

Trong 1 phút bánh xe quay được 60.2 = 120 vòng

Chu vi bánh xe đạp là 600\pi .120 = 72000\pi \left( {mm} \right) = 72\pi \left( m \right)

Quãng đường mà người đi xe đạp đi được trong phút là:

3. Giá trị lượng giác của góc lượng giác

a) Đường tròn lượng giác

+ Đường tròn lượng giác là đường tròn có tâm tại gốc tọa độ, bán kính bằng 1, được định hướng và lấy điểm A(1; 0) làm điểm gốc của đường tròn.

+ Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \alpha (độ hoặc radian) là điểm M trên đường tròn lượng giác sao cho sd\left( {OA;OM} \right) = \alpha.

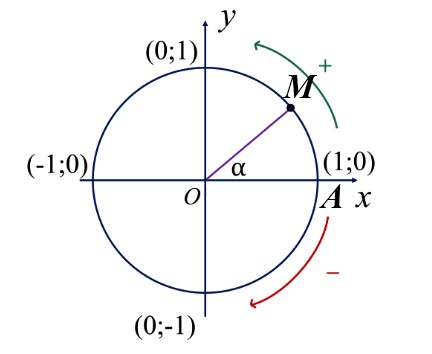
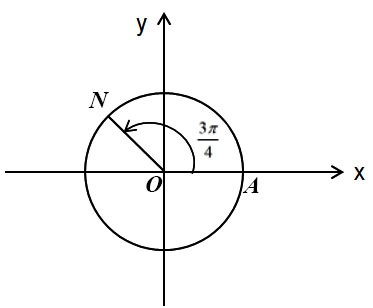
Giá trị lượng giác của góc lượng giác KNTT

Ví dụ: Trên đường tròn lượng giác, xác định điểm M và điểm N lần lượt biểu diễn các góc lượng giác {120^0};\frac{{3\pi }}{4}.

Hướng dẫn giải

Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo  bằng {120^0} được xác định trong hình vẽ:

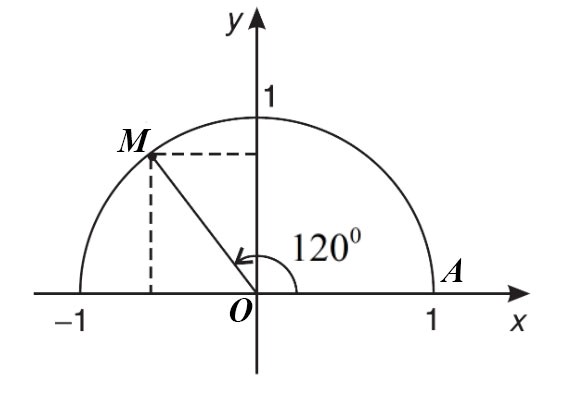
Giá trị lượng giác của góc lượng giác KNTT

Điểm N trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng \frac{{3\pi }}{4} được xác định trong hình:

Giá trị lượng giác của góc lượng giác KNTT

b) Các giá trị lượng giác của góc lượng giác

Giả sử điểm A\left( {x;y} \right) là điểm trên đường tròn lượng giác, biểu diễn góc lượng giác có số đo \alpha (như hình vẽ):

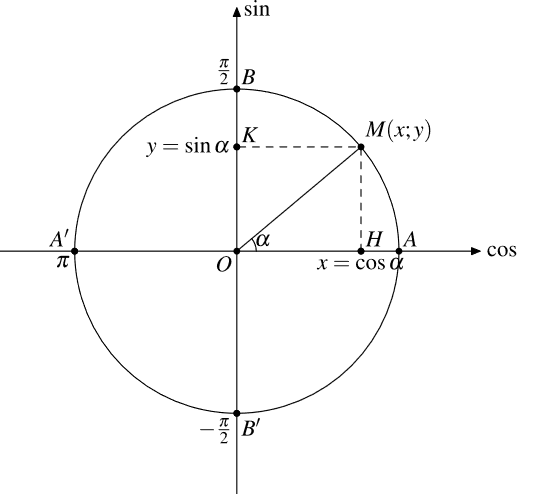
Giá trị lượng giác của góc lượng giác KNTT

  • Hoành độ x = \cos \alpha
  • Tung độ y = \sin \alpha
  • \tan \alpha = \frac{y}{x} = \frac{{\sin \alpha }}{{\cos \alpha }};\left( {x \ne 0} \right) hay \tan \alpha xác định khi \alpha \ne \frac{\pi }{2} + k\pi ;\left( {k \in \mathbb{Z}} \right)
  • \cot \alpha = \frac{x}{y} = \frac{{\cos \alpha }}{{\sin \alpha }};\left( {y \ne 0} \right) hay \cot \alpha xác định khi \alpha \ne k\pi ;\left( {k \in \mathbb{Z}} \right)

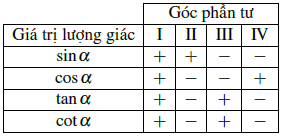
Chú ý: Dấu của các giá trị lượng giác của một góc lượng giác phụ thuộc vào vị trí điểm biểu diễn A trên đường tròn lượng giác.

Giá trị lượng giác của góc lượng giác KNTT

Ví dụ: Tính các giá trị lượng giác của góc lượng giác - \frac{\pi }{4}?

Hướng dẫn giải

Ta có:

\cos \left( {\frac{{ - \pi }}{4}} \right) = \frac{{\sqrt 2 }}{2}

\sin \left( {\frac{{ - \pi }}{4}} \right) = - \frac{{\sqrt 2 }}{2}

\tan \left( {\dfrac{{ - \pi }}{4}} \right) = \dfrac{{\sin \left( {\dfrac{{ - \pi }}{4}} \right)}}{{\cos \left( {\dfrac{{ - \pi }}{4}} \right)}} = \dfrac{{ - \dfrac{{\sqrt 2 }}{2}}}{{\dfrac{{\sqrt 2 }}{2}}} = - 1

\cot \left( {\dfrac{{ - \pi }}{4}} \right) = \dfrac{{\cos \left( {\dfrac{{ - \pi }}{4}} \right)}}{{\sin \left( {\dfrac{{ - \pi }}{4}} \right)}} = \dfrac{{\dfrac{{\sqrt 2 }}{2}}}{{ - \dfrac{{\sqrt 2 }}{2}}} = - 1

Ví dụ: Cho góc 0 < \alpha < \frac{\pi }{2}. Xét dấu biểu thức: A = \cos \left( {\alpha + \pi } \right) và B = \sin \left( {\alpha + \frac{{2\pi }}{5}} \right)?

Hướng dẫn giải

A = \cos \left( {\alpha + \pi } \right)

Ta có:

 0 < \alpha < \frac{\pi }{2} \Rightarrow \pi < \alpha + \pi < \frac{{3\pi }}{2} \Rightarrow \cos \left( {\alpha + \pi } \right) < 0

B = \sin \left( {\alpha + \frac{{2\pi }}{5}} \right)

0 < \alpha < \frac{\pi }{2} \Rightarrow \frac{{2\pi }}{5} < \alpha + \frac{{2\pi }}{5} < \frac{{9\pi }}{{10}} \Rightarrow \sin \left( {\alpha + \frac{{2\pi }}{5}} \right) > 0

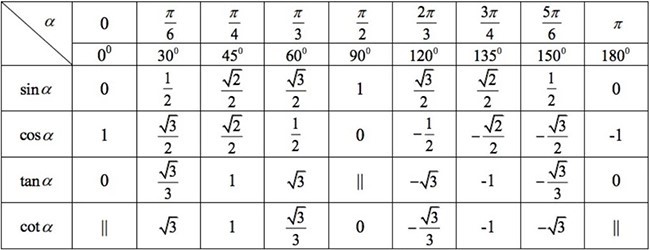
c) Giá trị lượng giác của các góc đặc biệt

Giá trị lượng giác của góc lượng giác KNTT

4. Quan hệ giữa các giá trị lượng giác

a) Các công thức lượng giác cơ bản

{\sin ^2}\alpha + {\cos ^2}\alpha = 1

1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }};\left( {\alpha \ne \frac{\pi }{2} + k\pi ;k \in \mathbb{Z}} \right)

1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }};\left( {\alpha \ne k\pi ;k \in \mathbb{Z}} \right)

\tan \alpha .\cot \alpha = 1;\left( {\alpha \ne \frac{{k\pi }}{2};k \in \mathbb{Z}} \right)

Ví dụ: Rút gọn biểu thức D = \tan x + \frac{{\cos x}}{{1 + \sin x}}

Hướng dẫn giải

Ta có:

D = \tan x + \frac{{\cos x}}{{1 + \sin x}}

= \frac{{\sin x}}{{\cos x}} + \frac{{\cos x}}{{1 + \sin x}}

= \frac{{\sin x\left( {1 + \sin x} \right) + {{\cos }^2}x}}{{\cos x\left( {1 + \sin x} \right)}}

= \frac{{\sin x + {{\sin }^2}x + {{\cos }^2}x}}{{\cos x\left( {1 + \sin x} \right)}}

= \frac{{\sin x + 1}}{{\cos x\left( {1 + \sin x} \right)}} = \frac{1}{{\cos x}}

b) Giá trị lượng giác của các góc có liên quan đặc biệt

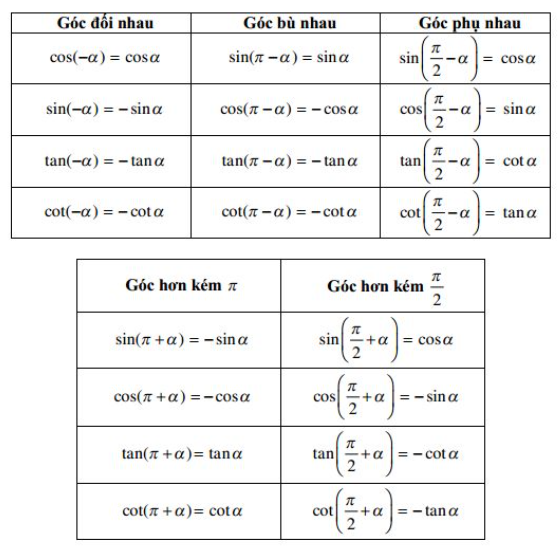
Giá trị lượng giác của góc lượng giác KNTT

Ví dụ: Biểu thức lượng giác {\left[ {\sin \left( {\frac{\pi }{2} - x} \right) + \sin \left( {10\pi + x} \right)} \right]^2} + {\left[ {\cos \left( {\frac{{3\pi }}{2} - x} \right) + \cos \left( {8\pi - x} \right)} \right]^2} có giá trị bằng bao nhiêu?

Hướng dẫn giải

Ta có:

\sin \left( {\frac{\pi }{2} - x} \right) = \cos x

\sin \left( {10\pi + x} \right) = \sin x

\cos \left( {\frac{{3\pi }}{2} - x} \right) = \cos \left( {2\pi - \frac{\pi }{2} - x} \right) = \cos \left( {\frac{\pi }{2} + x} \right) = - \sin x

\cos \left( {8\pi - x} \right) = \cos x

Khi đó

{\left[ {\sin \left( {\frac{\pi }{2} - x} \right) + \sin \left( {10\pi + x} \right)} \right]^2} + {\left[ {\cos \left( {\frac{{3\pi }}{2} - x} \right) + \cos \left( {8\pi - x} \right)} \right]^2}

= {\left( {\cos x + \sin x} \right)^2} + {\left( {\cos x - \sin x} \right)^2}

= \cos {x^2} + 2\sin x\cos x + {\sin ^2}x + {\cos ^2}x - 2\sin x\cos x + {\sin ^2}x = 2

Câu trắc nghiệm mã số: 44632,44629,44634
  • 82 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 KNTT