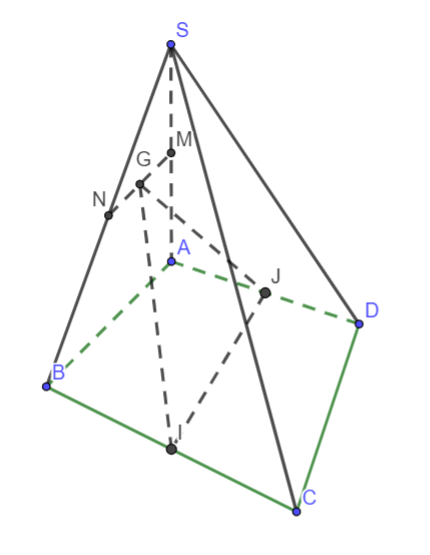
Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (GIJ) với hình chóp S.ABCD là hình bình hành.
Hướng dẫn:
Hình vẽ minh họa

Ta có ABCD là hình thang và I, J là trung điểm của AD và BC nên IJ là đường trung bình của hình thang ABCD
=> IJ // AB // CD
=> Trong (SAB) qua G kẻ MN // AB (M ∈ SA, N ∈ SB)
=> (SAB) ∩ (IJG) = MN và MN // IJ // AB // CD
Dễ thấy thiết diện của (IJG) và hình chóp là hình thang MNJI.
G là trọng tâm của tam giác SAB và MN // AB nên theo định lí Ta - lét ta có:
 (Với E là trung điểm của AB)
(Với E là trung điểm của AB)
=> 
Ta lại có: IJ là đường trung bình của hình thang ABCD nên: 
Để hình thang MNIJ trở thành hình bình hành thì điều kiện cần là MN = IJ
%20%5Chfill%20%5C%5C%0A%20%20%20%5CLeftrightarrow%20%5Cdfrac%7B1%7D%7B6%7DAB%20%3D%20%5Cdfrac%7B1%7D%7B2%7DCD%20%5Chfill%20%5C%5C%0A%20%20%20%5CLeftrightarrow%20AB%20%3D%203CD%20%5Chfill%20%5C%5C%20%0A%5Cend%7Bmatrix%7D)
(1)
(2)