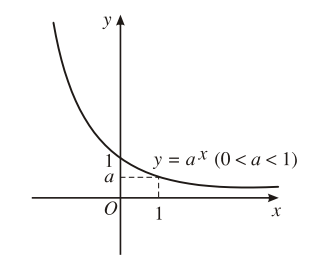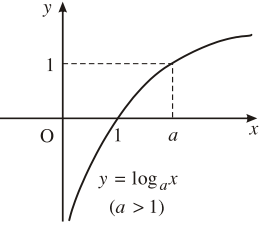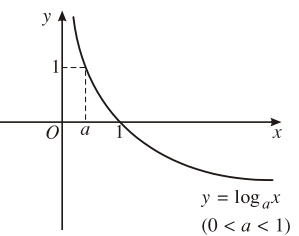Hàm số mũ và hàm số Lôgarit Kết nối tri thức
Bộ tài liệu Lí thuyết Toán 11 Kết nối tri thức: Hàm số mũ và hàm số Lôgarit bao gồm định nghĩa, tính chất và đồ thị hàm số của hàm số mũ và hàm số lôgarit. Ngoài ra có các bài tập ứng dụng có hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 11 KNTT giúp các em dễ dàng ôn tập củng cố.
1. Hàm số mũ
Định nghĩa: Cho số thực dương ![]() . Hàm số
. Hàm số ![]() được gọi là hàm số mũ cơ số
được gọi là hàm số mũ cơ số ![]() .
.
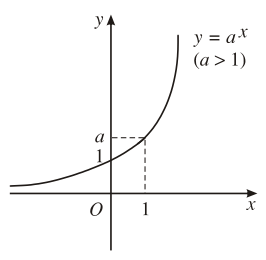
Tính chất biến thiên của hàm số mũ
|
|
|
|
| 1. Tập xác định |
|
|
| 2. Sự biến thiên | Đồng biến trên |
Nghịch biến trên |
| 3. Sự liên tục | ||
| 4. Giới hạn đặc biệt |  |
 |
|
5. Đồ thị hàm số |
Đồ thị luôn đi qua các điểm |
Đồ thị luôn đi qua các điểm |
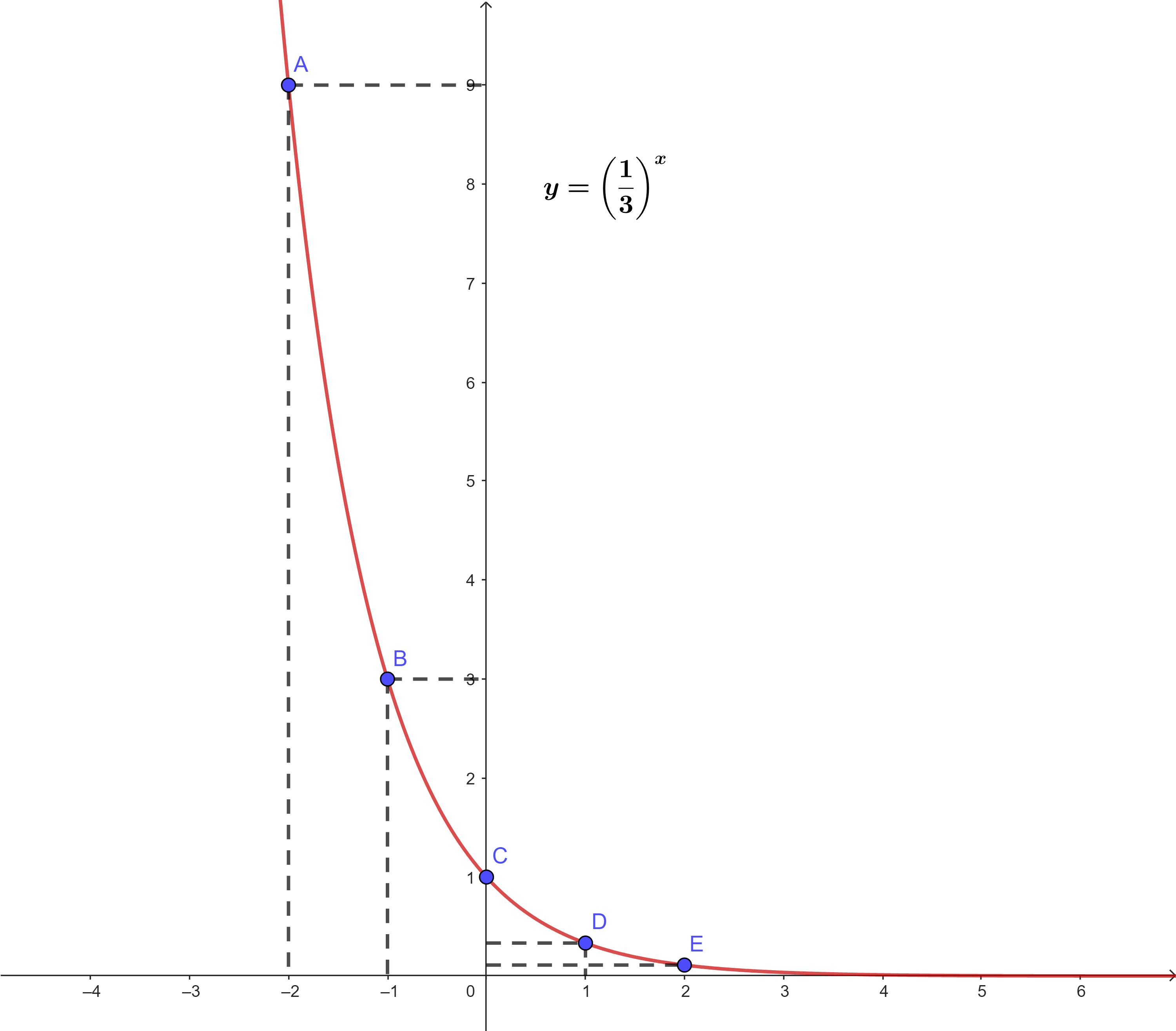
Ví dụ: Vẽ đồ thị hàm số ![]()
Hướng dẫn giải
Lập bảng giá trị của hàm số tại một số điểm như sau:
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
9 |
3 |
1 |
Đồ thị hàm số
2. Hàm số Lôgarit
Định nghĩa: Cho ![]() là số thực dương và
là số thực dương và ![]() .
.
Hàm số ![]() được gọi là hàm số lôgarit cơ số
được gọi là hàm số lôgarit cơ số ![]() .
.
Tính chất biến thiên của hàm số lôgarit
|
|
|
|
| 1. Tập xác định |
|
|
| 2. Sự biến thiên | Đồng biến trên |
Nghịch biến trên |
| 3. Sự liên tục | ||
| 4. Giới hạn đặc biệt |
|
|
|
5. Đồ thị hàm số |
Đi qua các điểm |
Đi qua các điểm |
Ví dụ: Tìm tập xác định của hàm số ![]() .
.
Hướng dẫn giải
Điều kiện xác định của hàm số ![]()

![]()
Vậy tập xác định của hàm số là ![]() .
.
Ví dụ: Cho đồ thị của ba hàm số ![]() như hình vẽ:
như hình vẽ:
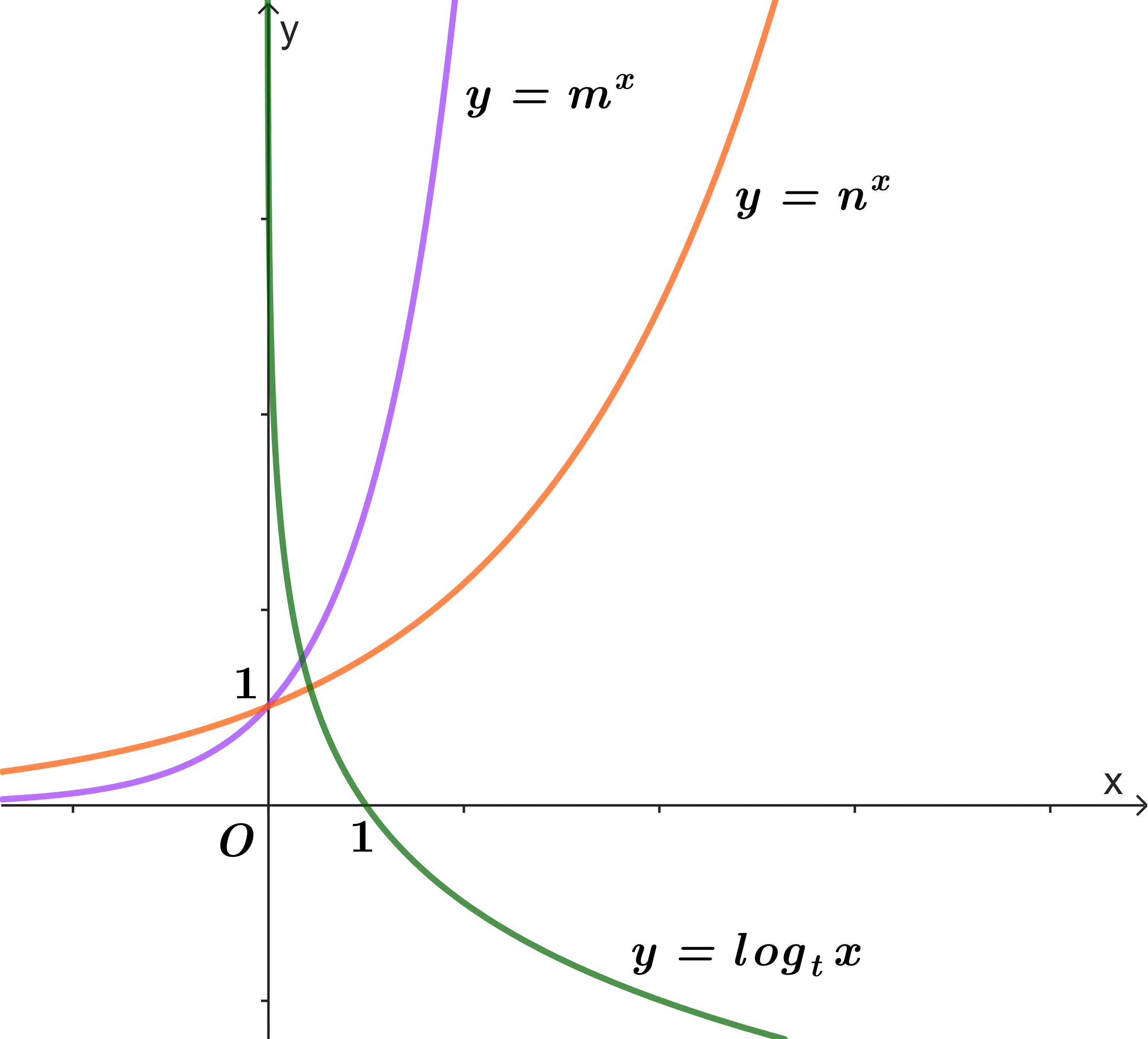
Tìm mối liên hệ giữa ![]() ?
?
Hướng dẫn giải:
Quan sát đồ thị ta thấy
Hàm số ![]() là hàm số đồng biến nên
là hàm số đồng biến nên ![]()
Hàm số ![]() là hàm số đồng biến nên
là hàm số đồng biến nên ![]()
Hàm số ![]() là hàm nghịch biến nên
là hàm nghịch biến nên ![]()
Vậy ta có: ![]()
Khi thay x = 1 vào hai hàm số ![]() ta thu được m > n
ta thu được m > n
Vậy ![]() .
.
Nội dung cùng chủ đề
-
Đề khảo sát chất lượng
-
Chương 1: Hàm số lượng giác và phương trình lượng giác
-
Chương 2: Dãy số. Cấp số cộng và cấp số nhân
-
Chương 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu ghép nhóm
-
Chương 4: Quan hệ song song trong không gian
-
Chương 5: Giới hạn. Hàm số liên tục
-
Chương 6: Hàm số mũ và hàm số lôgarit
-
Chương 7: Quan hệ vuông góc trong không gian
-
Chương 8: Các quy tắc tính xác suất
-
Chương 9: Đạo hàm
-
Đề thi Học kì
-
Đề thi giữa HK1
-
Đề thi Học kì 1
-
Đề thi học kì 1 Toán 11 Kết nối tri thức Đề 1
-
Đề thi học kì 1 Toán 11 Kết nối tri thức Đề 2
-
Đề thi học kì 1 Toán 11 Kết nối tri thức Đề 3
-
Đề thi học kì 1 Toán 11 Kết nối tri thức Đề 4
-
Đề thi học kì 1 Toán 11 Kết nối tri thức Đề 5
-
Đề thi học kì 1 Toán 11 Kết nối tri thức Đề 6
-
Đề thi học kì 1 Toán 11 Kết nối tri thức Đề 7
-
-
Đề thi giữa Học kì 2
-
Đề thi Học kì 2
-