Lớp 11 Toán 11 - Chân trời sáng tạo

Đường thẳng và mặt phẳng song song CTST

1. Đường thẳng song song với mặt phẳng

Cho đường thẳng d và mặt phẳng (P):

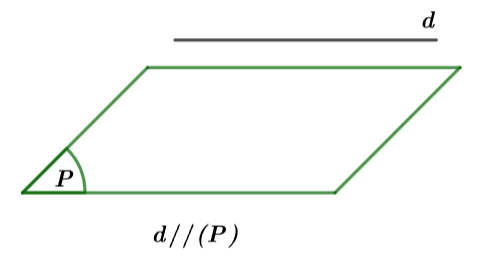
Trường hợp 1:

Nếu d và (P) không có điểm chung thì ta nói d song song với (P) hay (P) song song với d. Kí hiệu là d//(P) hay (P)//d.

 

Hình vẽ minh họa

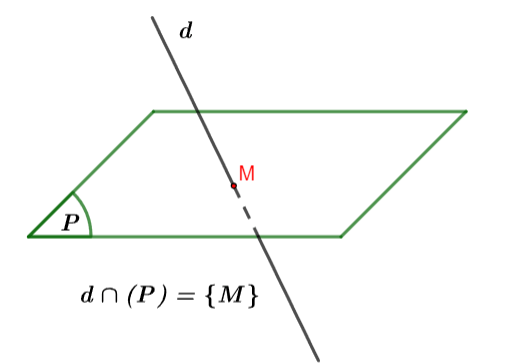
Đường thẳng và mặt phẳng song song CTST

Trường hợp 2:

Nếu d và (P) có một điểm chung duy nhất M thì ta nói d và (P) cắt nhau tại điểm M và kí hiệu là: d \cap \left( P \right) = \left\{ M \right\} hoặc d \cap \left( P \right) = M.

 

Hình vẽ minh họa

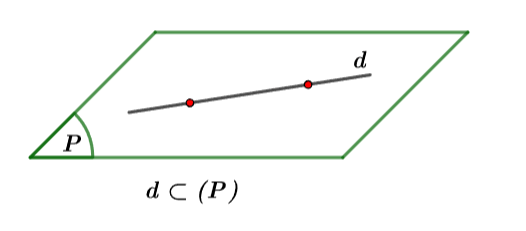
Đường thẳng và mặt phẳng song song CTST

Trường hợp 3:

Nếu d và (P) có nhiều hơn một điểm chung thì ta nói d nằm trong (P) hay (P) chứa d và kí hiệu là d \subset \left( P \right) hoặc \left( P \right) \supset d.

Hình vẽ minh họa

Đường thẳng và mặt phẳng song song CTST

Đường thẳng d song song với mặt phẳng (P) nếu chúng không có điểm chung.

2. Điều kiện để một đường thẳng song song với một mặt phẳng

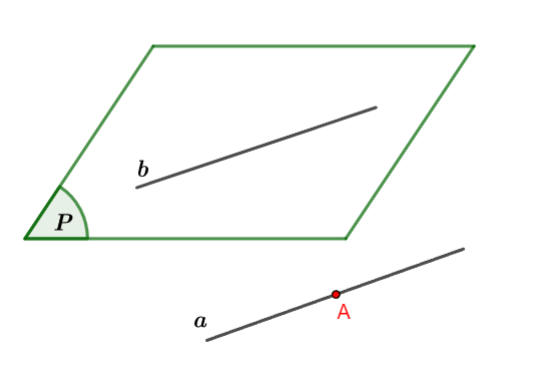
Định lí 1: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với đường thẳng b nào đó nằm trong (P) thì a song song với (P).

Hình vẽ minh họa

Đường thẳng và mặt phẳng song song CTST

3. Tính chất cơ bản của đường thẳng và mặt phẳng song song

Định lí 2: Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a, cắt (P) theo giao tuyến d thì a song song với d.

Hệ quả 1: Cho đường thẳng a song song với mặt phẳng (P). Nếu qua điểm M thuộc (P) ta vẽ đường thẳng b song song với a thì b phải nằm trong (P).

Hệ quả 2: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Ví dụ: Cho tứ diện ABCD. Giả sử G_1, G_2 lần lượt là trọng tâm tam giác ABD và ACD. Tìm giao tuyến của hai mặt phẳng (AG_1G_2) với mặt phẳng (ABC).

Hướng dẫn giải

Hình vẽ minh họa

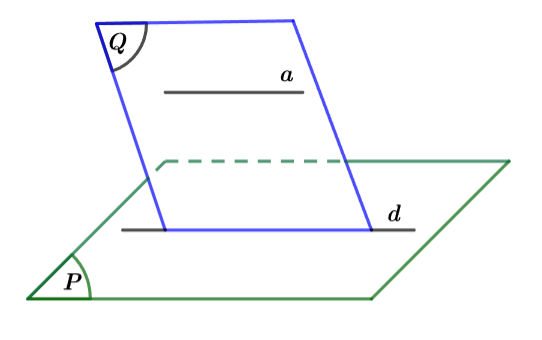
Đường thẳng và mặt phẳng song song CTST

Gọi M và N theo thứ tự là trung điểm của BD và CD.

Trong tam giác ΔAMN, ta có:

\frac{{A{G_1}}}{{AM}} = \frac{{A{G_2}}}{{AN}} = \frac{2}{3}\Rightarrow {G_1}{G_2}//MN

Do MN//BC;{G_1}{G_2}//MN

Mà \left\{ \begin{gathered} A \in \left( {A{G_1}{G_2}} \right) \cap \left( {ABC} \right) \hfill \\ {G_1}{G_2}//BC \hfill \\ \end{gathered} \right.

\Rightarrow \left( {A{G_1}{G_2}} \right) \cap \left( {ABC} \right) = Ax//{G_1}{G_2}//BC

Định lí 3: Nếu a và b là hai đường thẳng chéo nhau thì qua a, có một và chỉ một mặt phẳng song song với b.

Hình vẽ minh họa

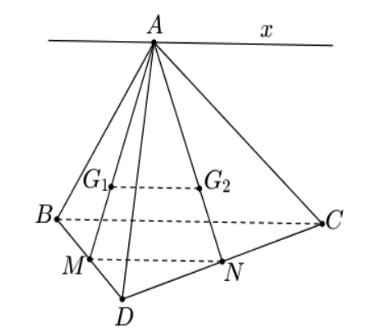
Đường thẳng và mặt phẳng song song CTST

Ví dụ: Cho tứ diện ABCD. Giả sử M thuộc đoạn thẳng BC. Xác định thiết diện của tứ diện ABCD cắt bởi mặt phẳng (α) qua M song song với AB và CD.

Hướng dẫn giải

Hình vẽ minh họa

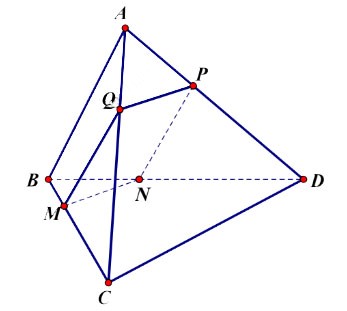
Đường thẳng và mặt phẳng song song CTST

Ta có:

(α) // AB nên giao tuyến của (α) với (ABC) là đường thẳng đi qua M và song song với AB và

cắt AC tại Q.

(α) // CD nên giao tuyến của (α) với (BCD) là đường thẳng đi qua M và song song với CD và

cắt BD tại N.

(α) // AB nên giao tuyến của (α) với (ABD) là đường thẳng đi qua N và song song với AB và

cắt AD tại P.

Ta có MN // PQ // CD // MQ // PN // AB

Vậy thiết diện là hình bình hành MNPQ.

Câu trắc nghiệm mã số: 34946,34940,34938
  • 9 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CTST