Lớp 11 Toán 11 - Chân trời sáng tạo

Hai mặt phẳng vuông góc CTST

1. Góc giữa hai mặt phẳng

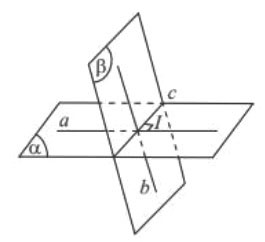
Góc giữa hai mặt phẳng (α) và (β) là góc giữa hai đường thẳng lần lượt vuông góc với (α) và (β). Kí hiệu là: ((α); (β)).

Hình vẽ minh họa

Hai mặt phẳng vuông góc CTST

2. Hai mặt phẳng vuông góc

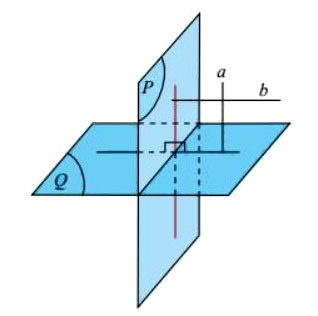
Hai mặt phẳng (P) và (Q) được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90^0. Kí hiệu là \left( P \right) \bot \left( Q \right).

Hình vẽ minh họa

Hai mặt phẳng vuông góc CTST

Chú ý: Nếu δ là góc giữa hai mặt phẳng (P) và (Q) thì {0^0} \leqslant \delta \leqslant {90^0}.

Điều kiện hai mặt phẳng vuông góc

Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Câu trắc nghiệm mã số: 9077

3. Tính chất cơ bản về hai mặt phẳng vuông góc

Định lí 1

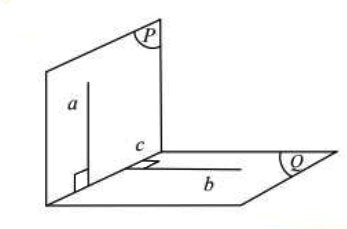
Nếu hai mặt phẳng vuông góc với nhau thì bất kì đường thẳng nào nằm trong mặt phẳng này mà vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.

Hình vẽ minh họa

Hai mặt phẳng vuông góc CTST

Định lí 2

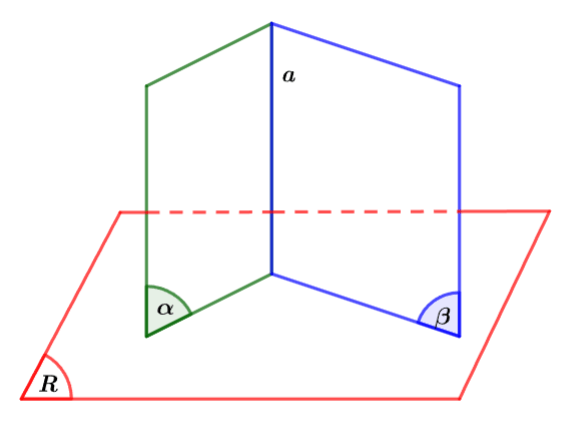
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

Hình vẽ minh họa

Hai mặt phẳng vuông góc CTST

Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 2a, AD = DC = a; cạnh bên SA = a và vuông góc với đáy. Mặt phẳng (α) qua SD và vuông góc với mặt phẳng (SAC). Tính diện tích (α) của thiết diện tạo bởi (α) với hình chóp đã cho.

Hướng dẫn giải

Hình vẽ minh họa:

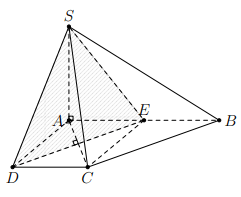
Hai mặt phẳng vuông góc CTST

Gọi E là trung điểm AB, suy ra AECD là hình vuông nên DE ⊥ AC (1)

Mặt khác SA ⊥ (ABCD) => SA ⊥ DE\text{ } (2)

Từ (1) và (2) suy ra DE ⊥ (SAC) => (SAD) ⊥ (SAC)

Ta có: \left\{ \begin{matrix} (SDE) \supset S \\ (SDE)\bot(SAC) \\ \end{matrix} ight.\ \Rightarrow (\alpha) \equiv (SDE)

Vậy thiết diện là tam giác SDE.

Ta có:

\begin{matrix} SD = \sqrt{SA^{2} + DA^{2}} = a\sqrt{2} \\ SE = \sqrt{SA^{2} + AE^{2}} = a\sqrt{2} \\ DE = AC = DC\sqrt{2} = a\sqrt{2} \\ \end{matrix}

Do đó tam giác SDE đều có cạnh a\sqrt 2 nên S_{SDE} = \frac{SD^{2}\sqrt{3}}{4} = \frac{a^{2}\sqrt{3}}{2}

Câu trắc nghiệm mã số: 9199

4. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương

a) Hình lăng trụ đứng

  • Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt đáy.
  • Hình lăng trụ đứng có các mặt bên là các hình chữ nhật và vuông góc với đáy.

Hình vẽ minh họa

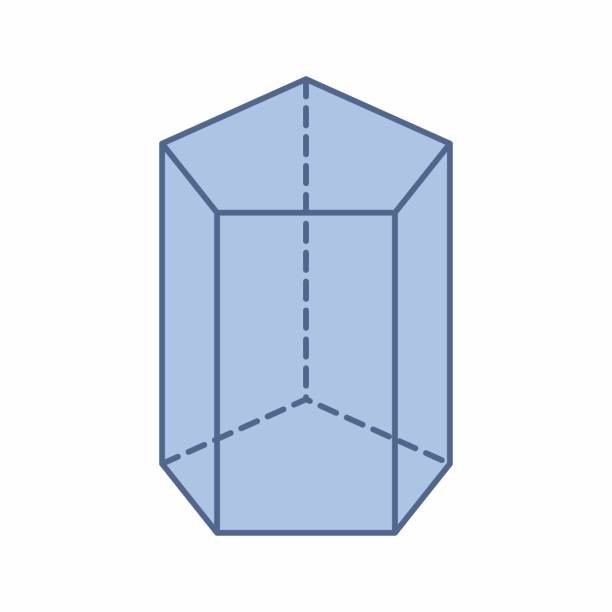
Hai mặt phẳng vuông góc CTST

b) Hình lăng trụ đều

  • Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.
  • Hình lăng trụ đều có các mặt bên là các hình chữ nhật có cùng kích thước.

Hình vẽ minh họa

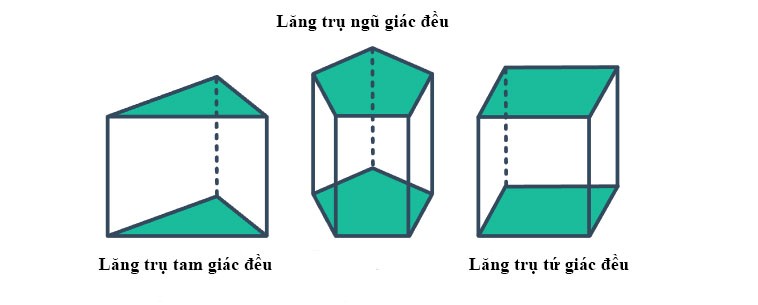
Hai mặt phẳng vuông góc CTST

c) Hình hộp đứng

  • Hình hộp đứng là hình lăng trụ đứng, có đáy là hình bình hành.
  • Hình hộp đứng có các mặt bên là các hình chữ nhật.

d) Hình hộp chữ nhật

  • Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.
  • Hình hộp chữ nhật có các mặt bên là hình chữ nhật.
  • Các đường chéo của hình hộp chữ nhật có độ dài bằng nhau và chúng cắt nhau tại trung điểm của mỗi đường.

Hình vẽ minh họa

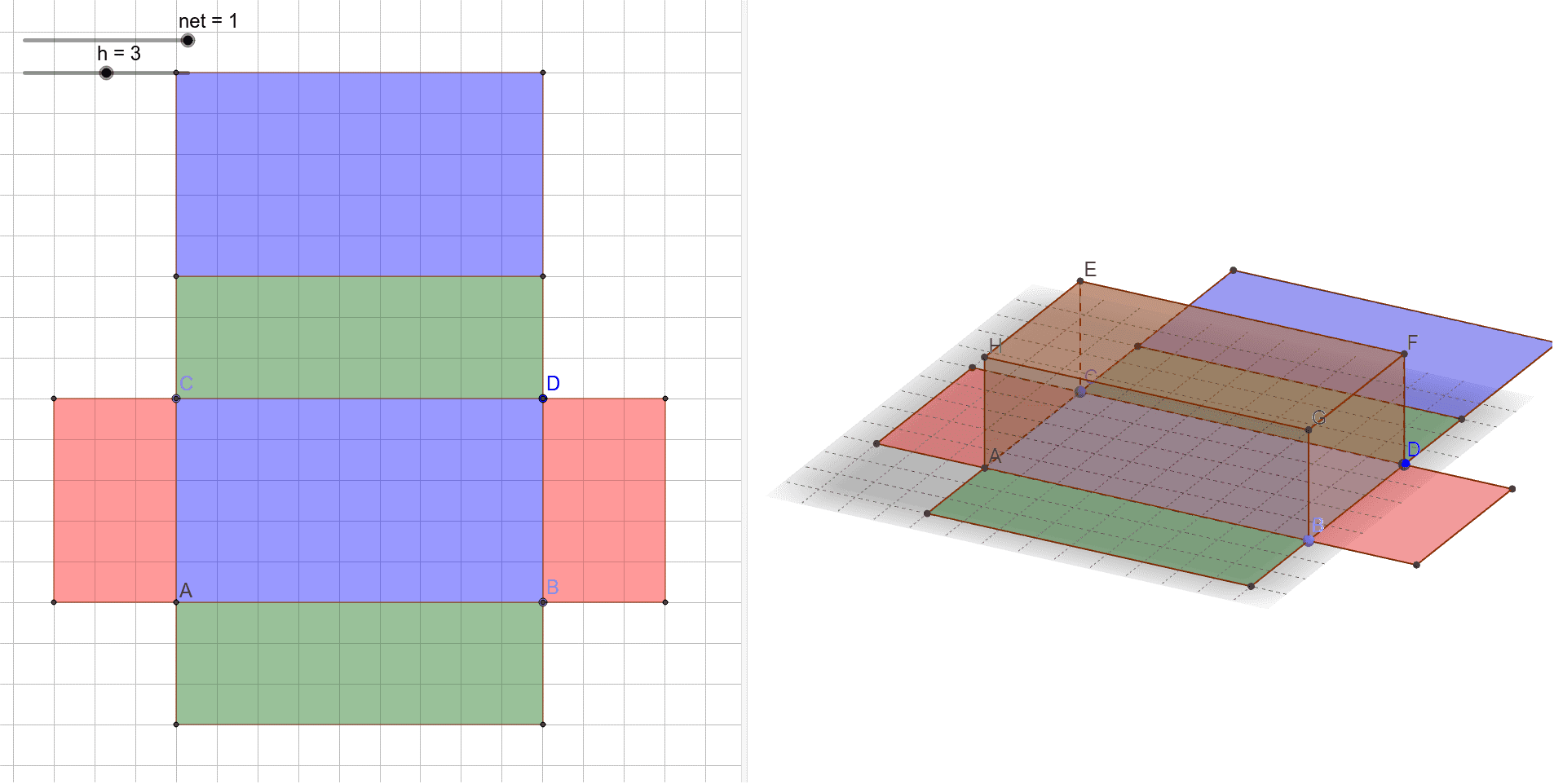
Hai mặt phẳng vuông góc CTST

e) Hình lập phương

  • Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau.
  • Hình lập phương có các mặt là hình vuông.

Hình vẽ minh họa

Hai mặt phẳng vuông góc CTST

5. Hình chóp đều. Hình chóp cụt đều

a) Hình chóp đều

Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.

Hình vẽ minh họa

Hai mặt phẳng vuông góc CTST

Một hình chóp là đều khi và chỉ khi đáy của nó là một hình đa giác đều và hình chiếu của đỉnh trên mặt phẳng đáy là tâm của mặt đáy.

Đặc điểm của hình chóp đều

  • Các mặt bên là các tam giác cân tại đỉnh hình chóp và bằng nhau.
  • Đoạn thẳng nối từ đỉnh hình chóp đến tâm của đáy thì vuông góc với mặt đáy và gọi là đường cao của hình chóp.
  • Độ dài đường cao là chiều cao của hình chóp đều.

Ví dụ: Cho hình chóp đều S.ABCD. Mặt phẳng   qua AB và vuông góc với mặt phẳng (SCD). Thiết diện tạo bởi   với hình chóp đã cho là hình gì? 

Hướng dẫn giải

Hình vẽ minh họa:

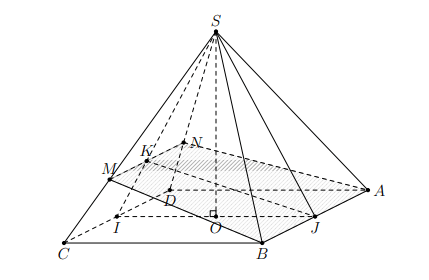
Hai mặt phẳng vuông góc CTST

Gọi I, J lần lượt là trung điểm của CD và AB.

Trong tam giác SIJ kẻ JK ⊥ SI.

Trong tam giác SIJ, qua K kẻ đường thẳng song song với CD cắt SC tại M, cắt SD tại N.

Ta dễ dàng chứng minh được (ABMN) ⊥ (SCD). Khi đó thiết diện cần tìm là hình thang ABMN. Vì hình chóp đã cho là hình chóp đều nên suy ra AN = BM.

Vậy thiết diện là hình thang cân.

b) Hình chóp cụt đều

Hình gồm các đa giác đều {A_1}{A_2}{A_3}...{A_n}.{B_1}{B_2}{B_3}...{B_n} và các hình thang cân {A_1}{A_2}{B_1}{B_2};{A_2}{A_3}{B_3}{B_2}; …; {A_n}{A_1}{B_1}{B_n} được tạo thành như hình vẽ được gọi là hình chóp cụt đều (nói đơn giản là hình chóp cụt được tạo thành từ hình chóp đều S.{A_1}{A_2}{A_3}...{A_n} sau khi cắt đi chóp đều S.{B_1}{B_2}{B_3}...{B_n}), kí hiệu là {A_1}{A_2}{A_3}...{A_n}.{B_1}{B_2}{B_3}...{B_n}.

Hình vẽ minh họa

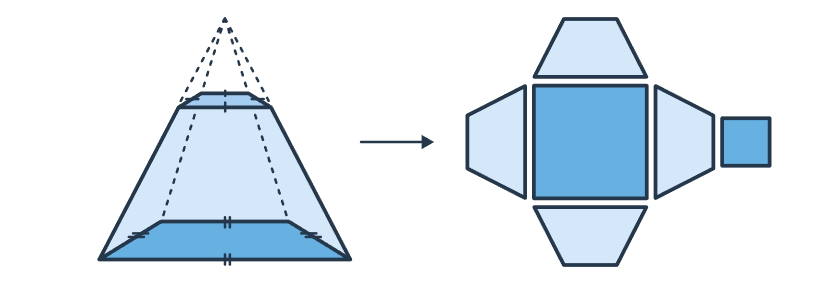
Hai mặt phẳng vuông góc CTST

Đặc điểm hình chóp cụt đều

  • Các đa giác {A_1}{A_2}{A_3}...{A_n};{B_1}{B_2}{B_3}...{B_n} được gọi là hai mặt đáy, các hình thang {A_1}{A_2}{B_1}{B_2};{A_2}{A_3}{B_3}{B_2}; …; {A_n}{A_1}{B_1}{B_n} được gọi là mặt bên của hình chóp cụt.
  • Các đoạn thẳng {A_1}{B_1};{A_2}{B_2};...;{A_n}{B_n} được gọi là các cạnh bên, cạnh của các mặt đáy được gọi là các cạnh đáy của hình chóp cụt.
  • Đoạn thẳng nối hai tâm của đáy được gọi là đường cao của hình chóp cụt đều. Độ dài của đường cao được gọi là chiều cao của hình chóp cụt.
  • 25 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CTST