Lớp 11 Toán 11 - Chân trời sáng tạo

Luyện tập Phương trình lượng giác cơ bản CTST

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Tìm giá trị nguyên của tham số m

    Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình \sqrt{3} \cos x + m - 1 = 0 có nghiệm:

    Hướng dẫn:

     Ta có:

    \sqrt 3 \cos x + m - 1 = 0 \Rightarrow \cos x = \frac{{1 - m}}{{\sqrt 3 }}

    Mặt khác \cos x \in \left[ { - 1;1} ight]

    Vậy để phương trình lượng giác có nghiệm thì

     \begin{matrix} \Rightarrow 1 - \sqrt 3 \leqslant m \leqslant 1 + \sqrt 3 \hfill \\ m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2} ight\} \hfill \\ \end{matrix}

    Vậy có 3 giá trị nguyên của tham số m thỏa mãn điều kiện đề bài.

  • Câu 2: Vận dụng
    Tìm số nghiệm của phương trình

    Với x thuộc \left ( 0;1  ight ) hỏi phương trình cos^{2}\left ( 6\pi x ight )=\frac{3}{4} có bao nhiêu nghiệm:

    Hướng dẫn:

     Giải phương trình:

    \begin{matrix} {\cos ^2}\left( {6\pi x} ight) = \dfrac{3}{4} \hfill \\ \Leftrightarrow \dfrac{{\cos \left( {12\pi x} ight) + 1}}{2} = \dfrac{3}{4} \hfill \\ \Leftrightarrow 2\cos \left( {12\pi x} ight) + 2 = 3 \hfill \\ \Leftrightarrow \cos \left( {12\pi x} ight) = \dfrac{1}{2} \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {12\pi x = \dfrac{\pi }{3} + k2\pi } \\ {12\pi x = - \dfrac{\pi }{3} + k2\pi } \end{array}} ight. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \dfrac{1}{{36}} + \dfrac{k}{6}} \\ {x = - \dfrac{1}{{36}} + \dfrac{k}{6}} \end{array}} ight.;\left( {k \in \mathbb{Z}} ight) \hfill \\ \end{matrix}

    Xét nghiệm {x = \frac{1}{{36}} + \frac{k}{6}}

    Do x \in \left( {0;1} ight) => 0 < \frac{1}{{36}} + \frac{k}{6} < 1 \Rightarrow k \in \left\{ {0;1;2;3;4;5} ight\}

    Xét nghiệm {x = -\frac{1}{{36}} + \frac{k}{6}}

    Do x \in \left( {0;1} ight) =>0 < -\frac{1}{{36}} + \frac{k}{6} < 1 \Rightarrow k \in \left\{ {1;2;3;4;5;6} ight\}

    Vậy có tất cả 12 giá trị x thỏa mãn

  • Câu 3: Thông hiểu
    Tìm điều kiện của tham số m thỏa mãn điều kiện

    Điều kiện để phương trình 3.sinx + m.cosx = 5 có nghiệm là:

    Hướng dẫn:

     Điều kiện để phương trình 3.sinx + m.cosx = 5 có nghiệm là

    \begin{matrix} {3^2} + {m^2} < {5^2} \hfill \\ \Leftrightarrow {m^2} < 16 \Leftrightarrow - 4 < m < 4 \hfill \\ \end{matrix}

    Vậy −4 < m < 4 thì phương trình đã cho có nghiệm.

  • Câu 4: Thông hiểu
    Giải phương trình

    Nghiệm của phương trình 2\sin^{2}x+5 \sin x + 3=0 là

    Hướng dẫn:

      \begin{matrix} 2{\sin ^2}x + 5\sin x + 3 = 0 \hfill \\ \Leftrightarrow \left( {\sin x + 1} ight).\left( {2\sin x + 3} ight) = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\sin x + 1 = 0} \\ {2\sin x + 3 = 0} \end{array}} ight. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\sin x = - 1} \\ {\sin x = - \dfrac{3}{2}\left( L ight)} \end{array}} ight. \hfill \\ \Rightarrow \sin x = - 1 \hfill \\ \Rightarrow x = - \dfrac{\pi }{2} + k2\pi ;\left( {k \in \mathbb{Z}} ight) \hfill \\ \end{matrix}

  • Câu 5: Thông hiểu
    Giải phương trình lượng giác

    Phương trình \sqrt{3} \sin 3x+\cos3x=-1

    Hướng dẫn:

     \begin{matrix} \sqrt 3 \sin 3x + \cos 3x = - 1 \hfill \\ \Leftrightarrow \dfrac{{\sqrt 3 }}{2}\sin 3x + \dfrac{1}{2}\cos 3x = - \dfrac{1}{2} \hfill \\ \Leftrightarrow \cos \dfrac{\pi }{6}.\sin 3x + \sin \dfrac{\pi }{6}.\cos 3x = - \dfrac{1}{2} \hfill \\ \Leftrightarrow \sin \left( {3x + \dfrac{\pi }{6}} ight) = - \dfrac{1}{2} \hfill \\ \end{matrix}

  • Câu 6: Thông hiểu
    Giải phương trình lượng giác

    Nghiệm của phương trình sinx + cosx = 1 là:

    Hướng dẫn:

     \begin{matrix} \sin x + \cos x = 1 \hfill \\ \Leftrightarrow \sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} ight) = 1 \hfill \\ \Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} ight) = \dfrac{1}{{\sqrt 2 }} \hfill \\ \Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} ight) = \sin \left( {\dfrac{\pi }{4}} ight) \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x + \dfrac{\pi }{4} = \dfrac{\pi }{4} + k2\pi } \\ {x + \dfrac{\pi }{4} = \pi - \dfrac{\pi }{4} + k2\pi } \end{array}} ight. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \dfrac{\pi }{4} - \dfrac{\pi }{4} + k2\pi } \\ {x = \pi - \dfrac{\pi }{4} - \dfrac{\pi }{4} + k2\pi } \end{array}} ight. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = k2\pi } \\ {x = \dfrac{\pi }{2} + k2\pi } \end{array}} ight.;\left( {k \in \mathbb{Z}} ight) \hfill \\ \end{matrix}

  • Câu 7: Vận dụng cao
    Biểu diễn nghiệm trên đường tròn lượng giác?

    Xét đường tròn lượng giác như hình vẽ. Biết \widehat {AOC} = \widehat {AOF} = 30^\circ, E và D lần lượt là các điểm đối xứng của C và F qua gốc O. Nghiệm của phương trình 2 \sin x -1 = 0 được biểu diễn trên đường tròn lượng giác là những điểm nào?

    Gợi ý:

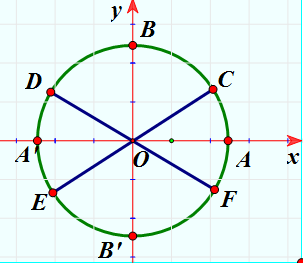
     Áp dụng Công thức lượng giác cơ bản của hàm sin(x); sau đó xét các nghiệm trên đường tròn lượng giác.

    Hướng dẫn:

     

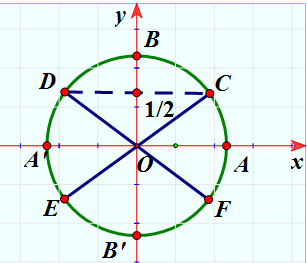
    Ta có: 2\sin x - 1 = 0 \Leftrightarrow \sin x = \frac{1}{2}

    \Leftrightarrow \left[ \begin{gathered} x = \frac{\pi }{6} + k2\pi \hfill \\ x = \frac{{5\pi }}{6} + k2\pi \hfill \\ \end{gathered} ight.\,\,\,,\,k \in \mathbb{Z}

    Dựa vào đường tròn lượng giác ta có điểm biểu diễn nghiệm của phương trình là điểm C và điểm D.

  • Câu 8: Nhận biết
    PT có tập nghiệm trùng?

    Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình {\tan ^2}x = 3?

    Gợi ý:

     Áp dụng giải phương trình bậc nhất đối với một hàm số lượng giác bằng cách sử dụng các công thức lượng giác cơ bản để biến đổi.

    Hướng dẫn:

     Ta có {\tan ^2}x = 3 \Leftrightarrow \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}} = 3 \Leftrightarrow {\sin ^2}x = 3{\cos ^2}x

    \Leftrightarrow 1 - {\cos ^2}x = 3{\cos ^2}x \Leftrightarrow 4{\cos ^2}x = 1

    Vậy {\tan ^2}x = 3 \Leftrightarrow 4{\cos ^2}x = 1.

  • Câu 9: Nhận biết
    Tìm PT tương đương

    Trong các phương trình sau, phương trình nào tương đương với phương trình 2{\cos ^2}x = 1?

    Gợi ý:

     Áp dụng giải phương trình bậc nhất đối với một hàm số lượng giác bằng cách sử dụng các công thức lượng giác cơ bản để biến đổi.

    Hướng dẫn:

    Ta có 2{\cos ^2}x = 1 \Leftrightarrow {\cos ^2}x = \frac{1}{2} . Mà {\sin ^2}x + {\cos ^2}x = 1 \to {\sin ^2}x = \frac{1}{2}.

    Do đó {\tan ^2}x = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}} = 1. Vậy 2{\cos ^2}x = 1 \Leftrightarrow {\tan ^2}x = 1.

  • Câu 10: Nhận biết
    Đếm số nghiệm trên đoạn

    Hỏi trên đoạn [0; 2023 \pi], phương trình \sqrt 3 \cot x - 3 = 0 có bao nhiêu nghiệm? 

    Gợi ý:

     Áp dụng Giải phương trình bậc nhất đối với một hàm số lượng giác, cụ thể là hàm cotang của f(x); sau đó xét nghiệm của x trên đoạn [0; 2023 \pi]

    Hướng dẫn:

     Ta có \cot x = \sqrt 3 \Leftrightarrow \cot x = \cot \frac{\pi }{6}

    \Leftrightarrow x = \frac{\pi }{6} + k\pi {\text{ }}\left( {k \in \mathbb{Z}} ight)

    Theo giả thiết, ta có

    0 \leqslant \frac{\pi }{6} + k\pi \leqslant 2023\pi \xrightarrow{{{\text{xap xi}}}} - \frac{1}{6} \leqslant k \leqslant 2022,833

    \xrightarrow{{k \in \mathbb{Z}}}k \in \left\{ {0;1;...;2022} ight\}.

    Vậy có tất cả 2023 giá trị nguyên của k tương ứng với có 2023 nghiệm thỏa mãn yêu cầu bài toán.

  • Câu 11: Nhận biết
    Đếm số vị trí biểu diễn điểm?

    Số vị trí biểu diễn các nghiệm của phương trình \tan \left( {2x - \frac{\pi }{3}} ight) + \sqrt 3 = 0 trên đường tròn lượng giác là?

    Gợi ý:

    Áp dụng Giải phương trình bậc nhất đối với một hàm số lượng giác, cụ thể là hàm tan của f(x)

    Hướng dẫn:

     Ta có \tan \left( {2x - \frac{\pi }{3}} ight) + \sqrt 3 = 0 \Leftrightarrow \tan \left( {2x - \frac{\pi }{3}} ight) = - \sqrt 3

    \Leftrightarrow \tan \left( {2x - \frac{\pi }{3}} ight) = \tan \left( { - \frac{\pi }{3}} ight)

    \Leftrightarrow 2x - \frac{\pi }{3} = - \,\frac{\pi }{3} + k\pi

    \Leftrightarrow 2x = k\pi \Leftrightarrow x = \frac{{k\pi }}{2}{\text{ }}\left( {k \in \mathbb{Z}} ight)

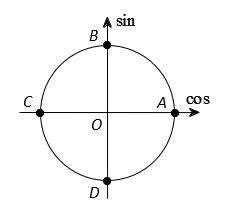
    Ta xét có 4 vị trí biểu diễn các nghiệm của phương trình đã cho trên đường tròn lượng giác là A, B, C, D.

  • Câu 12: Nhận biết
    Có phải là 1 nghiệm

    Hỏi x = \frac{{7\pi }}{3} là một nghiệm của phương trình nào sau đây?

    Gợi ý:

    Áp dụng Giải phương trình bậc nhất đối với một hàm số lượng giác, cụ thể là hàm sin(x) và cosin(x)

    Hướng dẫn:

     Với x = \frac{{7\pi }}{3}, suy ra \left\{ \begin{gathered} \sin x = \sin \frac{{7\pi }}{3} = \frac{{\sqrt 3 }}{2} \hfill \\ \cos x = \cos \frac{{7\pi }}{3} = \frac{1}{2} \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} 2\sin x - \sqrt 3 = 0 \hfill \\ 2\cos x - 1 = 0 \hfill \\ \end{gathered} ight.

  • Câu 13: Thông hiểu
    Tìm nghiệm dương nhỏ nhất

    Tìm nghiệm dương nhỏ nhất của phương trình 2\sin \left( {4x - \frac{\pi }{3}} ight) - 1 = 0.

    Gợi ý:

    Áp dụng Giải phương trình bậc nhất đối với một hàm số lượng giác, cụ thể là hàm sin của f(x).

    Hướng dẫn:

     Ta có 2\sin \left( {4x - \frac{\pi }{3}} ight) - 1 = 0 \Leftrightarrow \sin \left( {4x - \frac{\pi }{3}} ight) = \frac{1}{2}

    \Leftrightarrow \sin \left( {4x - \frac{\pi }{3}} ight) = \sin \frac{\pi }{6}

    \Leftrightarrow \left[ \begin{gathered} 4x - \frac{\pi }{3} = \frac{\pi }{6} + k2\pi \hfill \\ 4x - \frac{\pi }{3} = \pi - \frac{\pi }{6} + k2\pi \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left[ \begin{gathered} 4x = \frac{\pi }{2} + k2\pi \hfill \\ 4x = \frac{{7\pi }}{6} + k2\pi \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = \frac{\pi }{8} + \frac{{k\pi }}{2} \hfill \\ x = \frac{{7\pi }}{{24}} + \frac{{k\pi }}{2} \hfill \\ \end{gathered} ight.{\text{ }}\left( {k \in \mathbb{Z}} ight).

    TH1. Với x = \frac{\pi }{8} + \frac{{k\pi }}{2}\xrightarrow{{{\text{Cho}} > 0}}\frac{\pi }{8} + \frac{{k\pi }}{2} > 0

    \Leftrightarrow k > - \frac{1}{4} \to {k_{\min }} = 0 \Rightarrow x = \frac{\pi }{8}

    TH2. Với x = \frac{{7\pi }}{{24}} + \frac{{k\pi }}{2}\xrightarrow{{{\text{Cho}} > 0}}\frac{{7\pi }}{{24}} + \frac{{k\pi }}{2} > 0

    \Leftrightarrow k > - \frac{7}{{12}} \to {k_{\min }} = 0 \Rightarrow x = \frac{{7\pi }}{{24}}

    So sánh hai nghiệm ta được x = \frac{\pi }{8} là nghiệm dương nhỏ nhất.

  • Câu 14: Nhận biết
    Tìm tập nghiệm

    Tập nghiệm của phương trình \sin \left( {x + \frac{\pi }{4}} ight) = \frac{{\sqrt 3 }}{2}là?

    Gợi ý:

     Áp dụng Công thức lượng giác cơ bản của hàm sin (f(x)).

    Hướng dẫn:

     Ta có:   \sin \left( {x + \frac{\pi }{4}} ight) = \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{gathered} x + \frac{\pi }{4} = \frac{\pi }{3} + k2\pi \hfill \\ x + \frac{\pi }{4} = \pi - \frac{\pi }{3} + k2\pi \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left[ \begin{gathered} x = \frac{\pi }{{12}} + k2\pi \hfill \\ x = \frac{{5\pi }}{{12}} + k2\pi \hfill \\ \end{gathered} ight.\left( {k \in \mathbb{Z}} ight)

     

  • Câu 15: Thông hiểu
    Đếm số nghiệm

    Số nghiệm của phương trình \sin \left( {2x - {{40}^0}} ight) = \frac{{\sqrt 3 }}{2} với - {180^0} \leqslant x \leqslant {180^0} là?

    4 || Bốn || bốn || 4 nghiệm

    Đáp án là:

    Số nghiệm của phương trình \sin \left( {2x - {{40}^0}} ight) = \frac{{\sqrt 3 }}{2} với - {180^0} \leqslant x \leqslant {180^0} là?

    4 || Bốn || bốn || 4 nghiệm

     Phương trình \sin \left( {2x - {{40}^0}} ight) = \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {2x - {{40}^0}} ight) = \sin {60^0}

    \Leftrightarrow \left[ \begin{gathered} 2x - {40^0} = {60^0} + k{360^0} \hfill \\ 2x - {40^0} = {180^0} - {60^0} + k{360^0} \hfill \\ \end{gathered} ight.\,

    \Leftrightarrow \left[ \begin{gathered} 2x = {100^0} + k{360^0} \hfill \\ 2x = {160^0} + k{360^0} \hfill \\ \end{gathered} ight.\,

    \Leftrightarrow \left[ \begin{gathered} x = {50^0} + k{180^0} \hfill \\ x = {80^0} + k{180^0} \hfill \\ \end{gathered} ight.

    • TH1: Xét nghiệm x = {50^0} + k{180^0}:

    Vì - {180^0} \leqslant x \leqslant {180^0}\xrightarrow{{}} - {180^0} \leqslant {50^0} + k{180^0} \leqslant {180^0}

    \Leftrightarrow - \frac{{23}}{{18}} \leqslant k \leqslant \frac{{13}}{{18}}\xrightarrow{{k \in \mathbb{Z}}}\left[ \begin{gathered} k = - 1 \to x = - {130^0} \hfill \\ k = 0 \to x = {50^0} \hfill \\ \end{gathered} ight..

    • TH2: Xét nghiệm x = {80^0} + k{180^0}:

    Vì - {180^0} \leqslant x \leqslant {180^0}\xrightarrow{{}} - {180^0} \leqslant {80^0} + k{180^0} \leqslant {180^0}

    \Leftrightarrow - \frac{{13}}{9} \leqslant k \leqslant \frac{5}{9}\xrightarrow{{k \in \mathbb{Z}}}\left[ \begin{gathered} k = - 1 \to x = - {100^0} \hfill \\ k = 0 \to x = {80^0} \hfill \\ \end{gathered} ight..

    Vậy có tất cả 4 nghiệm thỏa mãn bài toán.

     

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (40%):
    2/3
  • Thông hiểu (40%):
    2/3
  • Vận dụng (13%):
    2/3
  • Vận dụng cao (7%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 20 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CTST

Đăng nhập