Hình chóp lục giác có bao nhiêu mặt?
Hình chóp có 7 mặt trong đó có 6 mặt bên và 1 mặt đáy.
Cho tứ diện 
. Gọi lần lượt là trung điểm của và là trọng tâm của tam giác . Giao điểm của đường thẳng và mặt phẳng là:
Hình vẽ minh họa
Ta có:
=> Giao điểm của đường thẳng và mặt phẳng
là giao điểm của đường thẳng
và
.
Thiết diện của hình chóp khi cắt bởi mặt phẳng tùy ý thể là:
Vì số mặt của hình chóp là 5 nên thiết diện tối đa chỉ có 5 cạnh.
=> Không thể là lục giác.
Cho tứ diện . Gọi lần lượt là trung điểm của các cạnh và . Mặt phẳng qua cắt lần lượt tại . Biết cắt tại . Ba điểm nào sau đây thẳng hàng?
Hình vẽ minh họa
Ta có:
Mà
Vậy ba điểm thẳng hàng.
Cho hình chóp có đáy là hình bình hành tâm . Gọi lần lượt là trung điểm của . Gọi là giao điểm của và . Giao điểm của với là điểm . Hãy chọn cách xác định điểm đúng nhất trong bốn phương án sau.
Hình vẽ minh họa
Trong mặt phẳng gọi
.
Mà nên
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
Khẳng định “Ba điểm phân biệt” là sai. Ba điểm phân biệt không thẳng hàng mới xác định một mặt phẳng duy nhất.
Khẳng định “Một điểm và một đường thẳng” sai. Điểm không nằm trên đường thẳng mới xác định một mặt phẳng duy nhất.
Khẳng định “Hai đường thẳng cắt nhau” đúng.
Khẳng định “Bốn điểm phân biệt” sai.
Một hình chóp có tổng số đỉnh và số cạnh bằng . Tìm số cạnh của đa giác đáy?
Một hình chóp có đáy là đa giác cạnh thì có
đỉnh và
cạnh
Tổng số đỉnh và số cạnh bằng 14
=> Số cạnh đáy của hình chóp là: 4.
Cho . Số mặt phẳng chứa tất cả các đỉnh của tam giác là:
Do ba điểm không thẳng hàng nên chỉ có một và chỉ một mặt phẳng đi qua chúng.
Cho tứ diện . Trên , lần lượt lấy hai điểm sao cho cắt tại . Tìm giao tuyến của hai mặt phẳng và .
Hình vẽ minh họa:
Ta có: là điểm chung của hai mặt phẳng
và
Ta lại có: nên
là điểm chung thứ hai.
Vậy giao tuyến của hai mặt phẳng và
là
Có bao nhiêu hình chóp tứ giác trong các hình sau?
Có 2 hình chóp tứ giác
Cho hình chóp có đáy là hình bình hành tâm . Gọi là trung điểm của và là giao điểm của và mặt phẳng . Khẳng định nào sau đây đúng?
Hình vẽ minh họa
Trong mặt phẳng gọi
mà
và
là trọng tâm tam giác
Cho hình chóp . Trong các khẳng định sau, khẳng định nào đúng?
Hình vẽ minh họa
Khẳng định đúng là “ và
là hai đường thẳng chéo nhau.”
Khẳng định nào sau đây đúng khi nói về mặt phẳng?
Theo cách xác định mặt phẳng thì “Có duy nhất một mặt phẳng chứa hai đường thẳng cắt nhau”.
Cho tứ diện . Gọi là trung điểm cạnh , lấy điểm trên cạnh sao cho . Giao tuyến của hai mặt phẳng và đi qua giao điểm của hai đường nào trong các cặp đường thẳng sau?
Hình vẽ minh họa
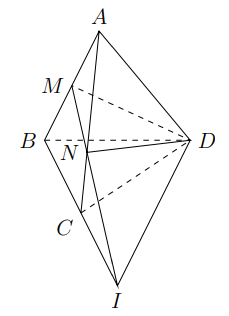
Gọi I là giao điểm của MN và BC.
Giao tuyến cần tìm là DI.
Do đó giao tuyến ấy đi qua giao điểm của MN và BC.
Cho tứ diện . Gọi lần lượt là trung điểm các cạnh và ; là trọng tâm tam giác . Khi đó giao điểm của đường thẳng và là
Hình vẽ minh họa
Trong gọi
, mà
