Lớp 11 Toán 11 - Chân trời sáng tạo

Đường thẳng vuông góc với mặt phẳng CTST

1. Đường thẳng vuông góc với mặt phẳng

Định nghĩa

Đường thẳng d được gọi là vuông góc với mặt phẳng (α) nếu nó vuông góc với mọi đường thẳng a nằm trong (α), kí hiệu: d \bot \left( \alpha \right).

Hình vẽ minh họa

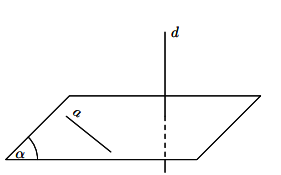
Đường thẳng vuông góc với mặt phẳng

Định lí 1

Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (α) thì d \bot \left( \alpha \right).

Hình vẽ minh họa

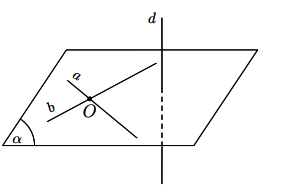
Đường thẳng vuông góc với mặt phẳng CTST

Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC,SB = SD. Chứng minh rằng:

a) SO \bot \left( {ABCD} \right)

b) AC \bot \left( {SBD} \right);BD \bot \left( {SAC} \right)

Hướng dẫn giải

Hình vẽ minh họa

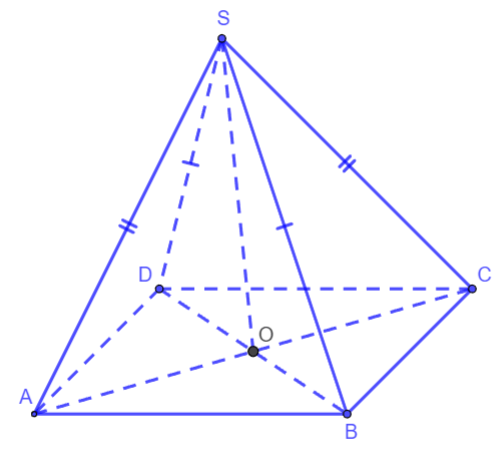
Đường thẳng vuông góc với mặt phẳng CTST

a) Vì O là giao điểm của AC và BD nên O là trung điểm của AC và BD

Theo bài ra ta có:

SA = SC nên tam giác SAC cân tại S

SO là đường trung tuyến tam giác SAC suy ra SO cũng là đường cao hay SO \bot AC

Tương tự ta có: SB = SD nên tam giác SBD cân tại S

SO là đường trung tuyến tam giác SBD suy ra SO cũng là đường cao hay SO \bot BD

Suy ra \left\{ \begin{gathered} SO \bot AC \hfill \\ SO \bot BD \hfill \\ AC \cap BD \equiv \left\{ O \right\} \hfill \\ AC,BD \subset \left( {ABCD} \right) \hfill \\ \end{gathered} \right.\Rightarrow SO \bot \left( {ABCD} \right)\Rightarrow AC \bot \left( {SBD} \right)

b) Ta có: \left\{ \begin{gathered} AC \bot BD \hfill \\ AC \bot SO \hfill \\ BD \cap SO \equiv \left\{ O \right\} \hfill \\ BD,SO \subset \left( {SBD} \right) \hfill \\ \end{gathered} \right.\Rightarrow BD \bot \left( {SAC} \right)

Lại có: \left\{ \begin{gathered} BD \bot AC \hfill \\ BD \bot SO \hfill \\ AC \cap SO \equiv \left\{ O \right\} \hfill \\ AC,SO \subset \left( {SAC} \right) \hfill \\ \end{gathered} \right.

Định lí 2

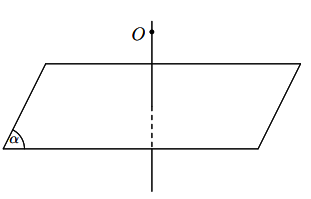
Có duy nhất một mặt phẳng đi qua một điểm và vuông góc với một đường thẳng cho trước.

Hình vẽ minh họa

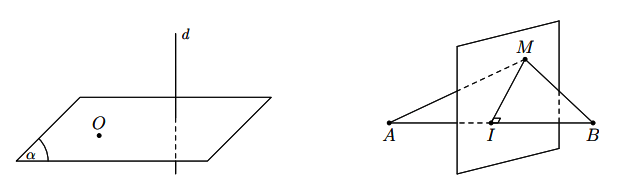
Đường thẳng vuông góc với mặt phẳng CTST

Có duy nhất một đường thẳng đi qua một điểm và vuông góc với một mặt phẳng cho trước.

Hình vẽ minh họa

Đường thẳng vuông góc với mặt phẳng CTST

2. Liên hệ giữa tính chất song song và vuông góc của đường thẳng và mặt phẳng

Định lí 3

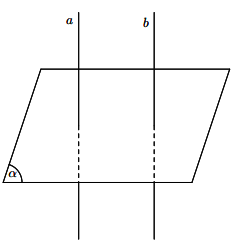
a) Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Hình vẽ minh họa

Đường thẳng vuông góc với mặt phẳng CTST

Định lí 4

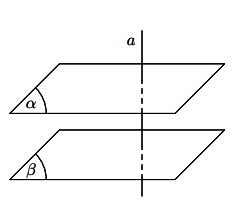
a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

Hình vẽ minh họa

Đường thẳng vuông góc với mặt phẳng CTST

Định lí 5

a) Cho đường thẳng a song song với mặt phẳng (α). Đường thẳng nào vuông góc với (α) thì cũng vuông góc với a.

b) Nếu đường thẳng a và mặt phẳng (α) (không chứa a) cùng vuông góc với một đường thẳng b thì chúng song song với nhau.

Ví dụ: Cho tứ diện SABC có đáy ABC là tam giác vuông tại A, SB = AB;SB \bot \left( {ABC} \right). Gọi H, I, K lần lượt là trung điểm của SA, BC, AB. Chứng minh rằng:

a) AC \bot \left( {SAB} \right)

b) BH \bot \left( {SAC} \right)

c) KI \bot SA

d) AB \bot IH

Hướng dẫn giải

Hình vẽ minh họa

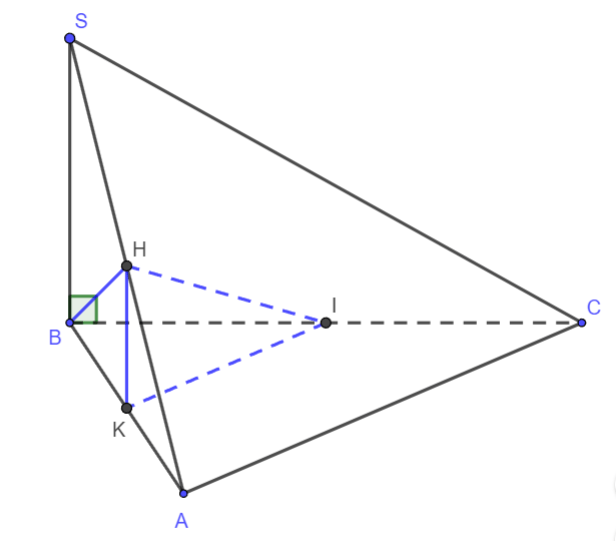
Đường thẳng vuông góc với mặt phẳng CTST

a) Ta có AC ⊥ AB (vì ∆ABC vuông tại A) và AC ⊥ SB (vì SB ⊥ (ABC)) suy ra AC ⊥ (SAB)

b) Vì SB ⊥ AB nên ∆SAB cân tại B

Mà H là trung điểm của SA suy ra BH ⊥ SA (1)

Ta cũng có AC ⊥ (SAB) và BH ⊥ (SAB) suy ra AC ⊥ BH (2)

Từ (1) và (2) suy ra BH ⊥ (SAC)

c) Xét ∆ABC có K, I lần lượt là trung điểm của AB, BC nên KI là đường trung bình của ∆ABC

Suy ra 

Ta lại có AC ⊥ (SAB) suy ra KI ⊥ (SAB) suy ra KI ⊥ SA.

d) Xét ∆SAB có H, K lần lượt là trung điểm của SA, AB nên HK là đường trung bình của ∆SAB

Suy ra HK // SB

Mặt khác SB ⊥ AB suy ra HK ⊥ AB (3)

Ta có KI ⊥ (SAB) suy ra KI ⊥ AB (4)

Từ (3) và (4) suy ra AB ⊥ (HIK) suy ra AB ⊥ IH.

3. Phép chiếu vuông góc

Định nghĩa

Cho mặt phẳng (P) và đường thẳng d vuông góc với (P). Phép chiếu song song theo phương của d lên mặt phẳng (P) được gọi là phép chiếu vuông góc lên (P).

Chú ý:

a) Phép chiếu vuông góc lên một mặt phẳng là một trường hợp đặc biệt của phép chiếu song song nên có đầy đủ các tính chất của phép chiếu song song.

b) Người ta còn dùng “phép chiếu (P)” thay cho “phép chiếu vuông góc lên (P)” và dùng (H’) là hình chiếu của (H) trên (P) thay cho (H’) là hình chiếu vuông góc của (H) trên (P).

Định lí ba đường vuông góc

Cho đường thẳng a nằm trong mặt phẳng (P) và b là đường thẳng không nằm trong (P) và không vuông góc với (P). Gọi b’ là hình chiếu vuông góc của b trên (P). Khi đó, a vuông góc với b khi và chỉ khi a vuông góc với b’.

Ví dụ: Cho hình chóp S.ABC có \widehat{BSC} = 120^{0};\widehat{CSA} = 60^{0};\widehat{ASB} = 90^{0} và SA = SB = SC. Gọi H là hình chiếu vuông góc của S trên mặt phẳng (ABC). Xác định vị trí điểm H?

Hướng dẫn giải

Hình vẽ minh họa:

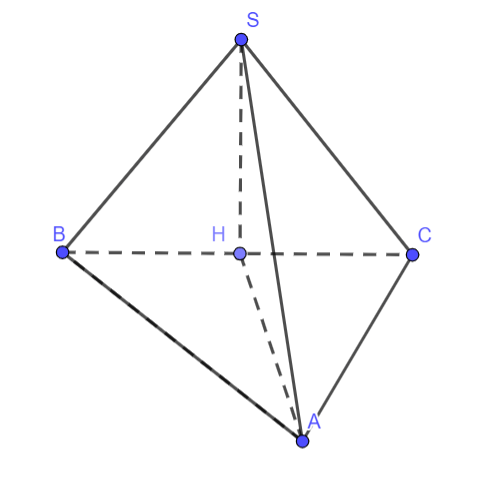
Đường thẳng vuông góc với mặt phẳng CTST

Đặt SA = a

Xét tam giác SAB vuông cân tại S ta có:

AB = \sqrt{SA^{2} + SB^{2}} = a\sqrt{2}

Xét tam giác SAC cân tại S ta có:

\widehat{CSA} = 60^{0} => SA = SC = AC = a

Áp dụng định lí cosin cho tam giác SBC ra có:

\begin{matrix}BC^{2} = SB^{2} + SC^{2} - 2SB.SC.cos\widehat{BSC} \hfill \\BC^{2} = a^{2} + a^{2} - 2a.a.cos120^{0} = 3a^{2} \hfill \\BC = a\sqrt{3} = \sqrt{AB^{2} + AC^{2}} \hfill \\\end{matrix}

Vậy tam giác ABC vuông tại A mà H là hình chiếu của S trên (ABC) nên H là tâm đường tròn ngoại tiếp tam giác ABC. Hay H là trung điểm của BC.

Câu trắc nghiệm mã số: 8992
  • 4 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CTST