Lớp 11 Toán 11 - Chân trời sáng tạo

Giới hạn của dãy số CTST

1. Giới hạn hữu hạn của dãy số

a) Giới hạn 0 của dãy số

Ta nói dãy số \left( {{u_n}} \right) có giới hạn 0 khi n dần tới dương vô cực, nếu \left| {{u_n}} \right| nhỏ hơn một số dương bất kì cho trước, kể từ một số hạng nào đó trở đi, kí hiệu \mathop {\lim }\limits_{n \to + \infty } {u_n} = 0 hay {u_n} \to 0 khi n \to + \infty. Ta còn viết là \lim {u_n} = 0.

Chú ý:

  • \lim \frac{1}{{{u^k}}} = 0,\left( {k \in {\mathbb{N}^*}} \right)
  • \lim {q^n} = 0;\left( {q \in \mathbb{R},\left| q \right| < 1} \right)

Ví dụ: Chứng minh rằng các dãy số có giới hạn là 0.

a) {u_n} = \frac{1}{{n\left( {2n + 3} \right)}}

b) {u_n} = \frac{{{n^n}{{\left( {n + 2} \right)}^n}}}{{{{\left( {2n + 2} \right)}^{2n}}}}

Hướng dẫn giải

a) Ta có:

\left| {\frac{1}{{n\left( {2n + 3} \right)}}} \right| = \left| {\frac{1}{{2{n^2} + 3n}}} \right| \leqslant \frac{1}{{{n^2}}}

Mà \lim \frac{1}{{{n^2}}} = 0 \Rightarrow \lim \frac{1}{{n\left( {2n + 3} \right)}} = 0

b) {u_n} = \frac{{{n^n}{{\left( {n + 2} \right)}^n}}}{{{{\left( {2n + 2} \right)}^{2n}}}} = \frac{{{{\left( {{n^2} + 2n} \right)}^n}}}{{{2^{2n}}{{\left( {n + 1} \right)}^{2n}}}}\leqslant \frac{{{{\left( {n + 1} \right)}^{2n}}}}{{{2^{2n}}{{\left( {n + 1} \right)}^{2n}}}} = {\left( {\frac{1}{2}} \right)^{2n}}

Mà \lim {\left( {\frac{1}{2}} \right)^{2n}} = 0 \Rightarrow \lim {u_n} = 0

b) Giới hạn hữu hạn của dãy số

Ta nói dãy số \left( {{u_n}} \right) có giới hạn hữu hạn là số a khi n dần tới dương vô cực, nếu \lim \left( {{u_n} - a} \right) = 0. Khi đó ta viết là \mathop {\lim }\limits_{n \to + \infty } {u_n} = a hay \lim {u_n} = a hay {u_n} \to a khi .

Chú ý: Nếu {u_n} = c,\left( {c = const} \right) thì \lim {u_n} = \lim c = c

Ví dụ: Chứng minh rằng \lim \frac{{6n + 2}}{{n + 5}} = 6

Hướng dẫn giải

Ta có: 

\lim \left( {\frac{{6n + 2}}{{n + 5}} - 6} \right) = \lim \left( {\frac{{ - 28}}{{n + 5}}} \right) = 0

(Do \left| {\frac{{28}}{{n + 5}}} \right| < \frac{{28}}{n})

Theo định nghĩa suy ra điều phải chứng minh.

2. Các phép toán về giới hạn hữu hạn của dãy số

Cho \mathop {\lim }\limits_{n \to + \infty } {u_n} = a;\mathop {\lim }\limits_{n \to + \infty } {v_n} = b và c  là hằng số khi đó:

\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + {v_n}} \right) = a + b \mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - {v_n}} \right) = a - b
\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}.{v_n}} \right) = a.b \mathop {\lim }\limits_{n \to + \infty } \left( {\frac{{{u_n}}}{{{v_n}}}} \right) = \frac{a}{b};\left( {b \ne 0} \right)
\mathop {\lim }\limits_{n \to + \infty } \left( {c.{u_n}} \right) = c.a Nếu \left\{ \begin{gathered} {u_n} \geqslant 0;\forall n \hfill \\ \mathop {\lim }\limits_{n \to + \infty } {u_n} = a \hfill \\ \end{gathered} \right. thì \left\{ \begin{gathered} a > 0 \hfill \\ \mathop {\lim }\limits_{n \to + \infty } \sqrt {{u_n}} = \sqrt a \hfill \\ \end{gathered} \right..

Ví dụ: Tính giới hạn:

a) \lim \frac{{n\sqrt n - 1}}{{n + n\sqrt n }}

b) \lim \frac{{3{n^2} - 2n + 5}}{{2{n^2} + 5n - 3}}

c) \lim \left( {\sqrt {{n^2} + 2n + 3} - n} \right)

d) \lim \frac{{{3^n} - {4^n} + {5^n}}}{{{3^n} + {4^n} - {5^n}}}

Hướng dẫn giải

a) \lim \frac{{n\sqrt n - 1}}{{n + n\sqrt n }} = \lim \frac{{{n^{\frac{3}{2}}} - 1}}{{n + {n^{\frac{3}{2}}}}} = \lim \dfrac{{1 - \dfrac{1}{{{n^{\frac{3}{2}}}}}}}{{\frac{1}{{{n^{\frac{1}{2}}}}} + 1}} = 1

b) \lim \dfrac{{3{n^2} - 2n + 5}}{{2{n^2} + 5n - 3}} = \lim \dfrac{{3 - \dfrac{2}{n} + \dfrac{5}{{{n^2}}}}}{{2 + \dfrac{5}{n} - \dfrac{3}{{{n^2}}}}} = \dfrac{3}{2}

c) \lim \left( {\sqrt {{n^2} + 2n + 3} - n} \right)

= \lim \frac{{\left( {\sqrt {{n^2} + 2n + 3} + n} \right)\left( {\sqrt {{n^2} + 2n + 3} - n} \right)}}{{\sqrt {{n^2} + 2n + 3} + n}}

= \lim \left( {\frac{{2n + 3}}{{\sqrt {{n^2} + 2n + 3} + n}}} \right)

= \lim \left( {\dfrac{{2 + \dfrac{3}{n}}}{{\sqrt {1 + \dfrac{2}{n} + \dfrac{3}{{{n^2}}}} + 1}}} \right) = 1

d) \lim \dfrac{{{3^n} - {4^n} + {5^n}}}{{{3^n} + {4^n} - {5^n}}} = \lim \dfrac{{\dfrac{{{3^n}}}{{{5^n}}} - \dfrac{{{4^n}}}{{{5^n}}} + 1}}{{\dfrac{{{3^n}}}{{{5^n}}} + \dfrac{{{4^n}}}{{{5^n}}} - 1}} = - 1

Câu trắc nghiệm mã số: 8213,8255

3. Tổng của cấp số nhân lùi vô hạn

Cấp số nhân vô hạn \left( {{u_n}} \right) có công bội q thỏa mãn \left| q \right| < 1 được gọi là cấp số nhân lùi vô hạn.

Cấp số nhân lùi vô hạn có tổng là:

S = {u_1} + {u_2} + ... + {u_n} = \frac{{{u_1}}}{{1 - q}}

Ví dụ minh họa cấp số nhân lùi vô hạn:

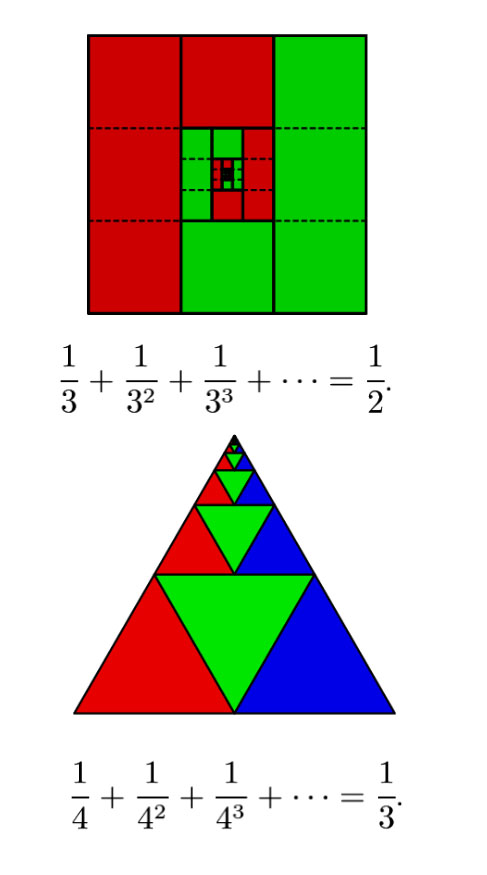
Giới hạn của dãy số CTST

Ví dụ: Tính tổng A = \frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{10}}}}

Hướng dẫn giải

Ta có:

A = \frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{10}}}}

\Leftrightarrow A + 1 = {\left( {\frac{1}{5}} \right)^{10}} + {\left( {\frac{1}{5}} \right)^9} + ... + \frac{1}{{{5^3}}} + \frac{1}{{{5^2}}} + \frac{1}{5} + 1

\Leftrightarrow \left( {A + 1} \right)\left( {\frac{1}{5} - 1} \right) = [{\left( {\frac{1}{5}} \right)^{10}} + {\left( {\frac{1}{5}} \right)^9} +... + \frac{1}{{{5^3}}} + \frac{1}{{{5^2}}} + \frac{1}{5} + 1]\left( {\frac{1}{5} - 1} \right)

\Leftrightarrow \frac{4}{5}.\left( {A + 1} \right) = {\left( {\frac{1}{5}} \right)^{10}} - 1

\Leftrightarrow A + 1 = \frac{{{{5.5}^{10}} - 1}}{{{{4.5}^{10}}}}

\Leftrightarrow A = \frac{{{{5.5}^{10}} - 1}}{{{{4.5}^{10}}}} - 1 \Leftrightarrow A = \frac{{{5^{10}} - 1}}{{{{4.5}^{10}}}} - 1

\Leftrightarrow A = \frac{1}{4}\left[ {1 - {{\left( {\frac{1}{5}} \right)}^{10}}} \right]

Câu trắc nghiệm mã số: 1309

4. Giới hạn vô cực

  • Ta nói dãy số \left( {{u_n}} \right) có giới hạn là + \infty nếu n \to + \infty lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi, kí hiệu \lim {u_n} = + \infty hay {u_n} \to + \infty khi n \to + \infty.
  • Ta nói dãy số \left( {{u_n}} \right) có giới hạn là - \infty khi n \to + \infty nếu \lim \left( { - {u_n}} \right) = + \infty kí hiệu là \lim {u_n} = - \infty hay {u_n} \to - \infty khi n \to + \infty.

Chú ý:

a) \lim {u_n} = + \infty khi và chỉ khi \lim \left( { - {u_n}} \right) = - \infty

b) Nếu \lim {u_n} = + \infty hoặc \lim {u_n} = - \infty thì \lim \frac{1}{{{u_n}}} = 0

c) Nếu \lim {u_n} = 0 và {u_n} > 0 với mọi n thì \lim \frac{1}{{{u_n}}} = + \infty

Ví dụ: Tính giới hạn:

a) \lim \left( {\sqrt[3]{{1 + 2n - {n^3}}} - n} \right)

b) \lim \left( {n + \sqrt {{n^2} - n + 1} } \right)

Hướng dẫn giải

a) \lim \left( {\sqrt[3]{{1 + 2n - {n^3}}} - n} \right)

= \lim \left[ {\sqrt[3]{{{n^3}\left( {\frac{1}{{{n^3}}} + \frac{2}{{{n^2}}} - 1} \right)}} - n} \right]

= \lim \left( { - 2n} \right) = - \infty

b) \lim \left( {n + \sqrt {{n^2} - n + 1} } \right)

= \lim \left( {n + n\sqrt {1 - \frac{1}{n} + \frac{1}{{{n^2}}}} } \right) = \lim \left( {2n} \right) = + \infty

Câu trắc nghiệm mã số: 8248,25809
  • 5 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CTST