Ôn tập chương 4 Đường thẳng và mặt phẳng. Quan hệ song song trong không gian

Trường hợp 1:

Hình vẽ minh hoạ

Nếu . Gọi

Nếu

=> Hình tạo bởi các giao tuyến của mặt phẳng với hình chóp là tứ giác

Nếu . Gọi

Hình tạo bởi các giao tuyến của mặt phẳng với hình chóp là tứ giác

Trường hợp 2:

Hình vẽ minh hoạ

Nếu . Hình tạo bởi các giao tuyến của mặt phẳng với hình chóp là tam giác .

Vậy hình tạo bởi các giao tuyến trên có thể là tứ giác hoặc tam giác.

Hình vẽ minh họa

Gọi

Ta thấy tam giác MIH là thiết diện của hình chóp cắt bởi mặt phẳng.

Ta có M, C lần lượt là trung điểm của AB, BE nên H là trọng tâm ∆ABE.

Suy ra . Chứng minh tương tự ta có: . Do đó ta có:

Tứ diện đều ABCD có cạnh bằng 1 nên

Áp dụng định lí cosin cho tam giác ta có:

Áp dụng công thức Hê- rông tính diện tích tam giác ta được:

Hình vẽ minh họa

Ta có:

và

Tương tự ta cũng có

Khi đó

=> Hình tạo bởi các giao tuyến của (α) với hình chóp là tam giác MNP.

Mệnh đề "Tồn tại duy nhất một đường thẳng qua một điểm và song song với một đường thẳng" sai vì nếu điểm đó thuộc đường thẳng đã cho thì không tồn tại đường thẳng nào đi qua điểm đó và song song với đường thẳng cho trước

Hình vẽ minh họa

Giả sử CM và DN đồng phẳng.

Khi đó, ta có A, B cùng thuộc mặt phẳng (MNDC)

=> A, B, C, D đồng phẳng, trái giả thiết ABCD là tứ diện.

Vậy CM và DN chéo nhau.

Hình vẽ minh họa

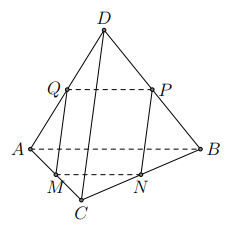
Gọi M, N, P, Q lần lượt là giao điểm của mặt phẳng chứa thiết diện với các cạnh AC, BC, BD, AD, khi đó theo giả thiết tứ giác MNPQ là hình thoi.

Cũng từ giả thiết ta suy ra nên ta có

Vậy cạnh của hình thoi là

Hình vẽ minh họa

Trong mặt phẳng (SAB), qua M kẻ đường thẳng song song với SI cắt SA tại P.

Trong mặt phẳng (ABC), qua M kẻ đường thẳng song song với IC cắt AC tại N.

Thiết diện là tam giác MNP.

Ta có:

Vậy hình tạo bởi các giao tuyến của mặt phẳng với tứ diện là tam giác MNP cân tại M.

Nếu thì a // b hoặc a, b chéo nhau.

Nếu thì a // b hoặc a ≡ b.

Nếu thì không kết luận được quan hệ giữa a và b.

Hình vẽ minh họa

Xét có lần lượt là trung điểm

=> là đường trung bình của

=> mà

Có vô số đường thẳng đi qua    và song song với    với điểm    không thuộc mặt phẳng  .

 Hình vẽ minh họa

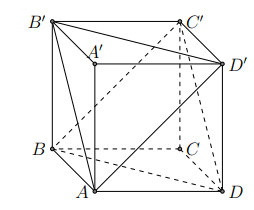
Mặt phẳng song song với mặt phẳng .

Vì và .

Hình vẽ minh họa

Ta có: MN // AC nên (MNP) ∩ (ACC’A’) = Px // AC // MN, gọi Q = Px ∩ AA’, Px ∩ OO’ = I.

Mà P là trung điểm của CC’ nên Q, I lần lượt là trung điểm của AA’, OO’.

Xét mặt phẳng (BDD’B’) gọi IJ ∩ B’D’ = H.

Theo tính chất đối xứng của hình lập phương và J là trung điểm của BO nên H là trung điểm của D’O’. (MNP) // AC // A’C’ nên (MNP) ∩ (A’B’C’D’) = Hy // A’C’.

Gọi E = Hy ∩ A’D’, F = Hy ∩ C’D’.

Khi đó hình tạo thành bởi các giao tuyến đó là lục giác MNPFEQ.

Khẳng định đúng là: “Nếu hai đường thẳng không có điểm chung thì hai đường thẳng đó song song hoặc chéo nhau.”

Hình vẽ minh họa:

Ta có:

, đi qua và .

Vậy giao tuyến của hai mặt phẳng và song song với đường thẳng .