Lớp 11 Toán 11 - Chân trời sáng tạo

Luyện tập Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Nhận biết
    Tính góc giữa đường thẳng A’B và mặt phẳng (A’B’C’)

    Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Góc giữa đường thẳng A’B và mặt phẳng (A’B’C’) bằng:

    Hướng dẫn:

    Hình vẽ minh họa:

    Vì BB’ ⊥ (A’B’C’) nên A’B’ là hình chiếu vuông góc của A’B lên (A’B’C’)

    => Góc giữa đường thẳng A’B và mặt phẳng (A’B’C’) là \widehat{BA'B'}

    Ta có: A’B’ = BB’ = a nên tam giác B’A’B vuông cân tại B’

    => \widehat{BA'B'} =45^{0}

  • Câu 2: Vận dụng
    Số đo góc hợp bởi đường thẳng SA và mặt phẳng (SDM)

    Cho hình chóp S.ABCD có ABCD là hình vuông, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm BC. Gọi \alpha là góc hợp bởi đường thẳng SA và mặt phẳng (SDM). Tính \alpha

    Hướng dẫn:

    + Không mất tính tổng quát, đặt AB = 2

    + Gọi N là trung điểm AB suy ra SN \bot AB \Rightarrow SN \bot \left( {ABCD} ight)

    + Gọi h = d\left( {A,\left( {SDM} ight)} ight) \Rightarrow \sin \alpha = \frac{h}{{SA}}

    Gọi I = DM \cap CN,\,J = AB \cap DM

    + Ta có \frac{{d\left( {A,\left( {SDM} ight)} ight)}}{{d\left( {N,\left( {SDM} ight)} ight)}} = \frac{{{\text{AJ}}}}{{NJ}} = \frac{4}{3}

    \Rightarrow h = d\left( {A,\left( {SDM} ight)} ight) = \frac{4}{3}d\left( {N,\left( {SDM} ight)} ight)

    + Ta có 

    \Delta CNB = \Delta DMC \Rightarrow \widehat {NCB} = \widehat {MDC}

    \Rightarrow \widehat {NCB} + \widehat {DMC} = \widehat {MDC} + \widehat {DMC} = 180^\circ - \widehat {MCD} = 90^\circ

    \Rightarrow DM \bot CN \Rightarrow DM \bot \left( {SNC} ight)

    + Gọi NH là đường cao \Delta SNI \Rightarrow NH \bot \left( {SDM} ight)

    \Rightarrow d\left( {N,\left( {SDM} ight)} ight) = NH

    + Tam giác NJI đồng dạng tam giác MBJ

    \begin{matrix} \Rightarrow \dfrac{{NI}}{{MB}} = \dfrac{{NJ}}{{MJ}} \hfill \\ \Rightarrow NI = \dfrac{{NJ}}{{MJ}}.MB = \dfrac{{NJ}}{{\sqrt {M{B^2} + B{J^2}} }} \hfill \\ MB = \dfrac{3}{{\sqrt {{1^2} + {2^2}} }}.1 = \dfrac{3}{{\sqrt 5 }} \hfill \\ \end{matrix}

    + Tam giác SAB là tam giác đều cạnh bằng 2 \Rightarrow SN = \sqrt 3

    \frac{1}{{N{H^2}}} = \frac{1}{{N{S^2}}} + \frac{1}{{N{I^2}}} \Rightarrow NH = \frac{{3\sqrt 2 }}{4}

    h = d\left( {A,\left( {SDM} ight)} ight) = \frac{4}{3}d\left( {N,\left( {SDM} ight)} ight) = \frac{4}{3}.\frac{{3\sqrt 2 }}{4} = \sqrt 2

    \Rightarrow \sin \alpha = \frac{h}{{SA}} = \frac{{\sqrt 2 }}{2} \Rightarrow \alpha = 45^\circ

  • Câu 3: Nhận biết
    Tính góc giữa SC với mặt phẳng (ABCD)

    Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA ⊥ (ABCD) , SA = a\sqrt{2}. Góc giữa SC với mặt phẳng (ABCD) là:

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có: \widehat{\left( SC,(ABCD) ight)}= \widehat{(SC,AC)} = \widehat{SCA}

    Lại có: \tan\widehat{SCA} = \frac{SA}{AC}= \frac{SA}{AB\sqrt{2}} = \frac{a\sqrt{2}}{a\sqrt{2}} = 1

    => \widehat{SCA} = 45^{0}

  • Câu 4: Nhận biết
    Tính góc giữa đường thẳng A’B và mặt phẳng (A’B’C’)

    Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Góc giữa đường thẳng A’B và mặt phẳng (A’B’C’) bằng:

    Hướng dẫn:

    Hình vẽ minh họa:

    Vì BB’ ⊥ (A’B’C’) nên A’B’ là hình chiếu vuông góc của A’B lên (A’B’C’)

    => Góc giữa đường thẳng A’B và mặt phẳng (A’B’C’) là \widehat{BA'B'}

    Ta có: A’B’ = BB’ = a nên tam giác B’A’B vuông cân tại B’

    => \widehat{BA'B'} =45^{0}

  • Câu 5: Thông hiểu
    Tính góc giữa đường thẳng SB và mặt phẳng đáy

    Cho hình chóp S.ABC có đáy là tam giác vuông tại C, SA vuông góc với mặt phẳng đáy, SA = a, AC = a, BC =a\sqrt{2}. Góc giữa đường thẳng SB và mặt phẳng đáy bằng:

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có:

    SA ⊥ (ABC) nên AB là hình chiếu của SA trên mặt phẳng (ABC)

    => \widehat{\left( SB,(ABC) ight)} =\widehat{(SB,\ AB)} = \widehat{SBA}

    Mặt khác có tam giác ABC vuông tại C:

    AB = \sqrt{AC^{2} + BC^{2}} =a\sqrt{3}

    \Rightarrow \tan\widehat{SBA} =\frac{SA}{AB} = \frac{1}{\sqrt{3}}

    \Rightarrow \widehat{SBA} =30^{0}

    Vậy (SB, (ABC)) = 300

  • Câu 6: Vận dụng
    Tính góc giữa hai đường thẳng

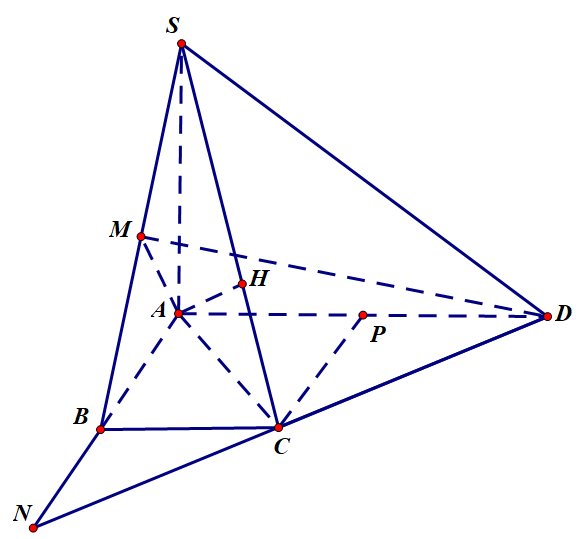
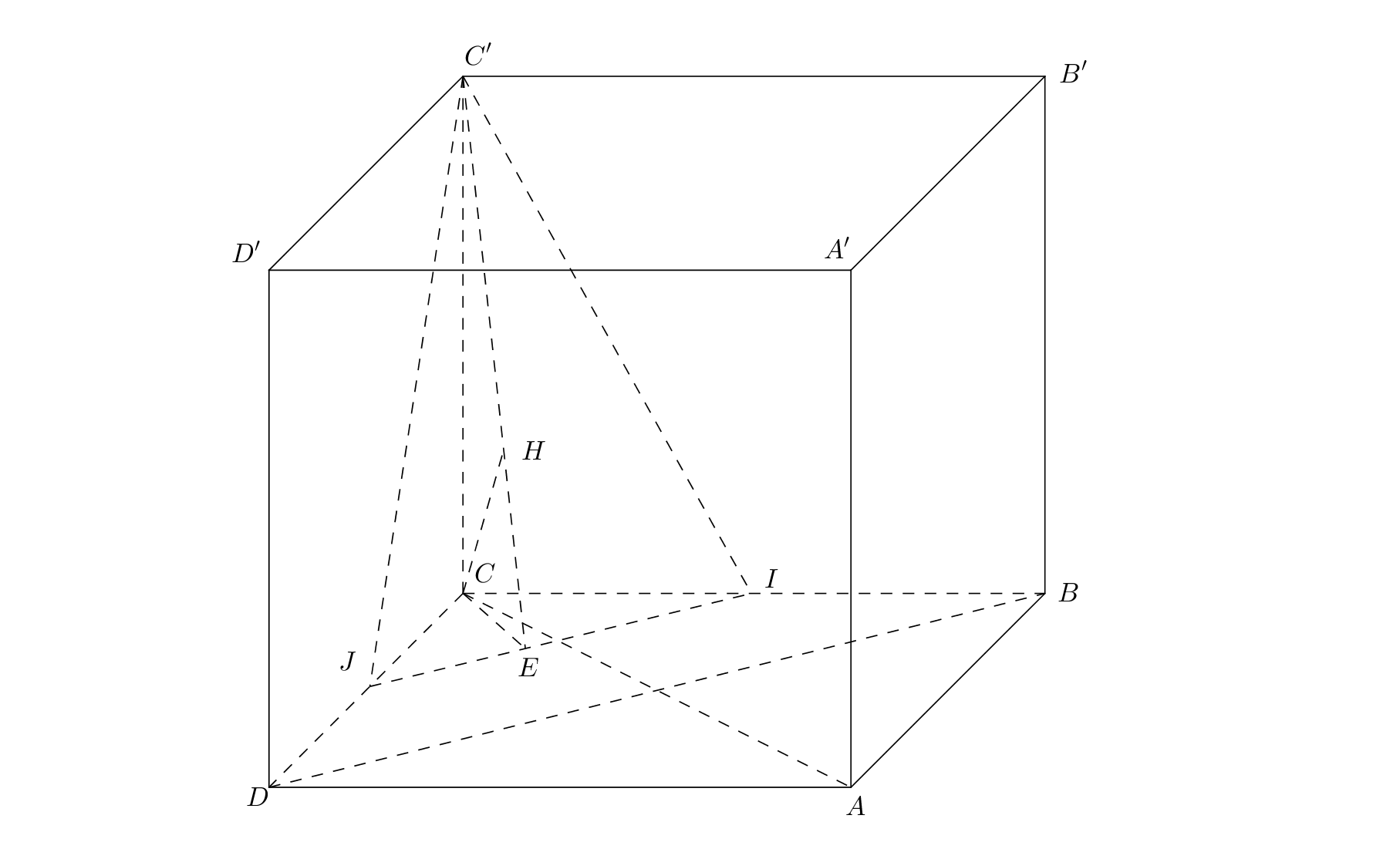
    Cho hình hộp ABCD.A’B’C’D’, A’B’C’D’ là hình chữ nhật tâmH, A’D’ = 2a, A'B' = 2\sqrt 3 a, H là hình chiếu vuông góc của A trên mặt phẳng (A’B’C’D’), AH = 2\sqrt 3 a. Gọi \alpha là góc giữa hai đường thẳng AD’ và DB’. Tính \cos \alpha.

    Hướng dẫn:

    Tính góc giữa hai đường thẳng

    Bước 1: Xác định góc giữa hai đường thẳng AD’ và DB’

    Kẻ đường thẳng d qua D, song song với AD', cắt A’D’ tại E

    Suy ra \alpha = \widehat {\left( {AD',\,DB'} ight)} = \widehat {\left( {DE,\,DB'} ight)}

    Bước 2: Tính \cos \alpha

    Kẻ đường thẳng qua H, song song với A’D’, cắt A’B’ tại F.

    Lấy điểm I sao cho ADIH là hình bình hành.

    Suy ra DI // AH , mà AH \bot \left( {A'B'C'D'} ight)

    => DI \bot \left( {A'B'C'D'} ight) \Rightarrow DI \bot IB'

    Ta có

    \begin{matrix} DE = AD' = \sqrt {A{H^2} + H{{D'}^2}} = \sqrt {{{\left( {2\sqrt 3 a} ight)}^2} + {{\left( {2a} ight)}^2}} = 4a \hfill \\ EB' = \sqrt {A'{E^2} + A'{{B'}^2}} = \sqrt {{4^2} + {{\left( {2\sqrt 3 } ight)}^2}} .a = 2\sqrt 7 a \hfill \\ IB' = \sqrt {I{F^2} + F{{B'}^2}} = \sqrt {{3^2} + {{\left( {\sqrt 3 } ight)}^2}} .a = 2\sqrt 3 a \hfill \\ DB' = \sqrt {D{I^2} + I{{B'}^2}} = \sqrt {{{\left( {2\sqrt 3 } ight)}^2} + {{\left( {2\sqrt 3 } ight)}^2}} .a = 2\sqrt 6 a \hfill \\ \end{matrix}

    Trong tam giác EDB’, có:

    \begin{matrix} \cos \widehat {EDB'} = \dfrac{{D{E^2} + D{{B'}^2} - E{{B'}^2}}}{{2.DE.DB'}} \hfill \\ = \dfrac{{{{\left( {4a} ight)}^2} + {{\left( {2\sqrt 6 a} ight)}^2} - {{\left( {2\sqrt 7 a} ight)}^2}}}{{2.4a.2\sqrt 6 a}} \hfill \\ = \dfrac{{\sqrt 6 }}{8} > 0 \hfill \\ \end{matrix}

    Suy ra \cos \alpha = \frac{{\sqrt 6 }}{8}

  • Câu 7: Vận dụng
    Tính sin của góc tạo bởi đường thẳng MD và mặt phẳng (SCD)

    Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AD = 2BC = 2AB = 2a, SA = 2a và SA vuông góc với ABCD. Gọi M là trung điểm SB và \varphi là góc tạo bởi đường thẳng MD và mặt phẳng (SCD). Khi đó \sin\varphi bằng:

    Hướng dẫn:

    Tính sin của góc tạo bởi đường thẳng MD và mặt phẳng (SCD)

    Ta có tam giác SAB vuông tại A nên AM = \frac{{2a}}{{\sqrt 5 }}

    Ta có: \left\{ \begin{gathered} AD \bot AB \hfill \\ A{\text{D}} \bot SA \hfill \\ \end{gathered} ight. \Rightarrow A{\text{D}} \bot \left( {SAB} ight) \Rightarrow A{\text{D}} \bot MA

    Xét tam giác MDA vuông tại A theo định lí Pytago ta có:

    MD = \sqrt {A{D^2} + A{M^2}} = \sqrt {4\,{a^2} + \frac{{4\,{a^2}}}{5}} = \frac{{2\sqrt {30} a}}{5}

    Ta có \frac{{{d_{\left( {M,\,\left( {SC{\text{D}}} ight)} ight)}}}}{{{d_{\left( {B,\,\left( {SC{\text{D}}} ight)} ight)}}}} = \frac{{SM}}{{SB}} = \frac{1}{2}

    Gọi N là giao của AB và CD. Gọi P là trung điểm AD nên ABCP là hình vuông

    => CP = a \Rightarrow CP = \frac{1}{2}AD

    Ta có (hai đường chéo hình vuông)

    Mặt khác BP // CD.

    Do đó tam giác ACD vuông tại nên tam giác ACN vuông tại C, mặt khác BC \bot AN nên B là trung điểm AN.

    Ta có AB giao (SCB) tại N nên

    \frac{{{d_{\left( {B,\,\left( {C{\text{SD}}} ight)} ight)}}}}{{{d_{\left( {A,\left( {SCA} ight)} ight)}}}} = \frac{{NB}}{{NA}} = \frac{1}{2} \Rightarrow {d_{\left( {M,\left( {SC{\text{D}}} ight)} ight)}} = \frac{1}{4}{d_{\left( {A,\left( {SCA} ight)} ight)}}

    Ta có \left\{ \begin{gathered} CD \bot AC \hfill \\ CD \bot SA \hfill \\ \end{gathered} ight. \Rightarrow CD \bot \left( {SAC} ight)

    Trong (SAC) kẻ AH \bot SC

    \Rightarrow AH \bot \left( {SC{\text{D}}} ight) \Rightarrow {d_{\left( {A,\left( {SC{\text{D}}} ight)} ight)}} = AH \Rightarrow {d_{\left( {M,\left( {SC{\text{D}}} ight)} ight)}} = \frac{1}{4}AH

    Xét tam giác SAC vuông tại A nên AH = \frac{{2a}}{{\sqrt 3 }}

    Do đó \sin \varphi = \frac{{{d_{\left( {M,\left( {SC{\text{D}}} ight)} ight)}}}}{{MD}} = \frac{{1AH}}{{4MD}}=\frac{{\sqrt {10} }}{{24}}

  • Câu 8: Nhận biết
    Xác định góc giữa SB và mặt phẳng (ABCD)

    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy. Góc giữa SB và mặt phẳng (ABCD) là góc giữa cặp đường thẳng nào sau đây?

    Hướng dẫn:

    Hình vẽ minh họa:

    Hai mặt phẳng (SAC) và (SBD) cắt nhau theo giao tuyến SO và cùng vuông góc với đáy nên SO ⊥ (ABCD).

    Vậy góc giữa SB và mặt phẳng (ABCD) là góc giữa SB và BD.

  • Câu 9: Thông hiểu
    Tính ϕ

    Cho hình chóp S.ABC có SA = SB = CA = CB. Tính ϕ là góc giữa SC và mặt phẳng (ABC), biết (SAB) vuông góc với (ABC):

    Hướng dẫn:

    Hình vẽ minh họa:

    Gọi H là trung điểm của AB, ta có SH ⊥ AB, CH ⊥ AB

    Mà (SAB) ⊥ (ABC) nên SH ⊥ (ABC)

    Suy ra \left\{ \begin{matrix}SH\bot CH \\\widehat{\left( SC,(ABC) ight)} = \widehat{SCH} \\\end{matrix} ight.

    Ta có:

    ∆SAB = ∆CAB (c.c.c)

    => SH = CH. Do đó ∆SCH vuông cân tại H

    Vậy \widehat{\left( SC,(ABC) ight)} =\widehat{SCH} = 45^{0}

  • Câu 10: Thông hiểu
    Tính tan α

    Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường MC’ và mặt phẳng (ABC). Khi đó tan α bằng bao nhiêu?

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có: CM là hình chiếu của C’M lên (ABC)

    => Góc giữa MC’ và (ABC) là góc giữa MC’ và MC.

    Xét tam giác MCC’ vuông tại C ta có:

    \tan\alpha = \dfrac{CC'}{MC} =\dfrac{a}{\dfrac{a\sqrt{3}}{2}} = \dfrac{2\sqrt{3}}{3}

  • Câu 11: Thông hiểu
    Tính tan góc giữa đường thẳng SA và mặt phẳng (SBC)

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SC vuông góc với đáy và SC = a\sqrt{3}. Tính tan góc giữa đường thẳng SA và mặt phẳng (SBC).

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có: \left\{ \begin{matrix}AB\bot SC \\AB\bot BC \\\end{matrix} ight.

    => AB ⊥ (SBC)

    Suy ra hình chiếu của SA lên (SBC) là SB

    => \widehat{\left( SA,(SBC) ight)} =\widehat{(SA,\ SB)} = \widehat{ASB}

    Trong tam giác SCB vuông tại C, ta có:

    SB = \sqrt{SC^{2} + CB^{2}} =\sqrt{4a^{2}} = 2a

    Trong tam giác SBA vuông tại B, ta có:

    \tan\widehat{BSA} = \frac{AB}{SB} =\frac{a}{2a} = \frac{1}{2}

    Vậy tan góc giữa đường thẳng SA và mặt phẳng (SBC) là \frac{1}{2}

  • Câu 12: Thông hiểu
    Tính góc giữa đường thẳng SA và mặt phẳng (SBD)

    Cho hình chóp S.ABCD có đáy là hình thoi cạnh 2a, \widehat{ABC} = 60^{0}, SA = a\sqrt{3} và SA ⊥ (ABCD). Tính góc giữa đường thẳng SA và mặt phẳng (SBD).

    Hướng dẫn:

    Hình vẽ minh họa:

    Vì tam giác ABC cân và có góc 600 nên nó là tam giác đều

    Gọi O là trung điểm của AC.

    Ta có: Hai mặt phẳng (SAC) và (SBD) vuông góc nhau theo giao tuyến SO

    => Hình chiếu vuông góc của SA lên mặt phẳng (SBD) là SO

    => \widehat{\left( SA,(SBD) ight)} =\widehat{(SA,\ SO)} = \widehat{ASO}

    Xét tam giác vuông SOA ta có: \left\{\begin{matrix}OA = \dfrac{AC}{2} = \dfrac{2a}{2} = a \\SA = a\sqrt{3} \\\end{matrix} ight.

    => \tan\widehat{OSA} = \frac{AO}{SA} =\frac{1}{\sqrt{3}} \Rightarrow \widehat{OSA} = 30^{0}

    Vậy góc giữa SA và mặt phẳng (SBD) bằng 300.

  • Câu 13: Thông hiểu
    Tan góc giữa đường thẳng BD’ và mặt phẳng (ADD’A’)

    Cho hình lập phương ABCD.A’B’C’D’. Tan góc giữa đường thẳng BD’ và mặt phẳng (ADD’A’) bằng bao nhiêu?

    Hướng dẫn:

    Hình vẽ minh họa:

    Do ABCD.A’B’C’D’ là hình lập phương nên BA ⊥ (ADD’A’)

    Do đó góc giữa đường thẳng BD’ và mặt phẳng (ADD’A’) là góc \widehat{BD'A}

    Gọi độ dài cạnh của hình lập phương là a

    Khi đó AB = a;AD' =a\sqrt{2}

    => \tan\widehat{BD'A} =\frac{AB}{AD'} = \frac{1}{\sqrt{2}}

    Vậy tan góc giữa đường thẳng BD’ và mặt phẳng (ADD’A’) là \frac{\sqrt{2}}{2}

  • Câu 14: Nhận biết
    Góc giữa đường thẳng SB và mặt phẳng đáy

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB = a, SA ⊥ (ABC), SA = a. Góc giữa đường thẳng SB và mặt phẳng đáy là:

    Hướng dẫn:

    Hình vẽ minh họa:

    Theo bài ta có AB là hình chiếu của SB trên (ABC)

    Vậy \widehat{\left( SB,(ABC) ight)} =\widehat{(SB,\ AB)} = \widehat{SBA}

    Mà ∆SBA vuông cân tại A nên \widehat{SBA}= 45^{0}

  • Câu 15: Vận dụng cao
    Giá trị lớn nhất của góc giữa đường thẳng và mặt phẳng

    Cho hình hộp chữ nhật ABCD.A’B’C’D’ nội tiếp mặt cầu (S) có bán kính R = \frac{{\sqrt {17} }}{2}. Gọi I; J là trung điểm BC, CD và \alpha là góc giữa đường thẳng AC’ và mặt phẳng (C’IJ). Giá trị lớn nhất của \sin \alpha là

    Hướng dẫn:

    Giá trị lớn nhất của góc giữa đường thẳng và mặt phẳng

    Đặt CD = a\,,\,CB = b\,,CC' = c\,\,\,\left( {a,b,c > 0} ight).

    AC{'^2} = {a^2} + {b^2} + {c^2} = 17.

    Gọi K là hình chiếu của A lên (C’IJ)

    \left( {\widehat {AC',\left( {C;{\text{IJ}}} ight)}} ight) = \left( {\widehat {AC',AK}} ight) = \alpha

    Ta có \sin \alpha = \frac{{d\left( {A,\left( {C'{\text{IJ}}} ight)} ight)}}{{AC'}} = \frac{{3d\left( {C,\left( {C'{\text{IJ}}} ight)} ight)}}{{\sqrt {17} }}

    Trong (ABCD) kẻ tại E

    \left\{ \begin{gathered} IJ \bot CE \hfill \\ IJ \bot CC\prime \hfill \\ CE \subset \left( {CEC'} ight) \hfill \\ \,CC' \subset \left( {CEC'} ight) \hfill \\ CE \cap CC' = C \hfill \\ \end{gathered} ight. \Rightarrow IJ \bot \left( {CEC'} ight) \Rightarrow \left( {C'IJ} ight) \bot \left( {CEC'} ight)

    Trong (CEC’) kẻ CH \bot C'E tại H

    Suy ra d\left( {C,\left( {C'{\text{IJ}}} ight)} ight) = CH = h

    Do đó \sin \alpha = \frac{{3h}}{{\sqrt {17} }}

    Ta có:

    \begin{matrix} \dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{4}{{{a^2}}} + \dfrac{4}{{{b^2}}} = \dfrac{1}{{{c^2}}} + 4\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} ight) \geqslant \dfrac{1}{{{c^2}}} + \dfrac{{16}}{{{a^2} + {b^2}}} \hfill \\ \Leftrightarrow \dfrac{1}{{{h^2}}} \geqslant \frac{1}{{{c^2}}} + \dfrac{{16}}{{17 - {c^2}}} = \dfrac{{17 - {c^2} + {c^2}}}{{17{c^2}}} + \dfrac{{16\left( {17 - {c^2} + {c^2}} ight)}}{{17\left( {17 - {c^2}} ight)}} \hfill \\ \Leftrightarrow \dfrac{1}{{{h^2}}} \geqslant \dfrac{{17 - {c^2}}}{{17{c^2}}} + \dfrac{{16{c^2}}}{{17\left( {17 - {c^2}} ight)}} + 1 \geqslant 2.\dfrac{4}{{17}} + 1 = \dfrac{{25}}{{17}} \Leftrightarrow h \leqslant \dfrac{{\sqrt {17} }}{5}. \hfill \\ \Rightarrow \sin \alpha \leqslant \dfrac{3}{5}. \hfill \\ \end{matrix}

    Vậy đạt giá trị lớn nhất là \frac{3}{5}

    Dấu xảy ra khi: \left\{ \begin{gathered} {a^2} = {b^2} = \frac{{34}}{5} \hfill \\ {c^2} = \frac{{17}}{5} \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} a = b = \sqrt {\frac{{34}}{5}} \hfill \\ c = \sqrt {\frac{{17}}{5}} \hfill \\ \end{gathered} ight.

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (33%):
    2/3
  • Thông hiểu (40%):
    2/3
  • Vận dụng (20%):
    2/3
  • Vận dụng cao (7%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 9 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CTST

Đăng nhập