Lớp 11 Toán 11 - Cánh Diều

Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất

A. Phép toán trên các biến cố

1. Biến cố hợp

Cho hai biến cố A và B. Khi đó A,B là các tập con của không gian mẫu \Omega. Đặt C = A \cup B, ta có C là một biến cố gọi là biến cố hợp của hai biến cố A và B, kí hiệu là A \cup B .

Hình vẽ minh họa

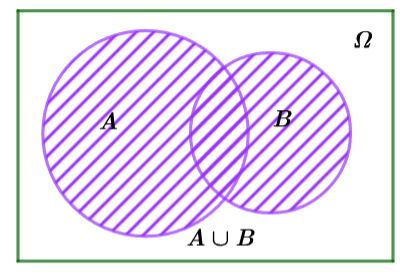
Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất

Chú ý: Biến cố C có thể phát biểu dưới dạng mệnh đề nêu sự kiện là “ A xảy ra hoặc B xảy ra” hay “có ít nhất một trong các biến cố A,B xảy ra”.

Ví dụ: Một lớp có 35 học sinh gồm 20 nam và 15 nữ. Chọn ngẫu nhiên hai học sinh để phân công trực nhật. Xét các biến cố sau:

A: “Hai học sinh được chọn đều là học sinh nam”.

B: “Hai học sinh được chọn đều là học sinh nữ”.

C: “Hai học sinh được chọn có cùng giới tính”.

Trong các biến cố đã cho, biến cố nào là biến cố hợp của hai biến cố còn lại?

Hướng dẫn giải

Biến cố C là biến cố hợp của hai biến cố A và B.

Câu trắc nghiệm mã số: 44163,44151

2. Biến cố giao

Cho hai biến cố A và B. Khi đó A,B là các tập con của không gian mẫu \Omega. Đặt D = A \cap B, ta có D là một biến cố gọi là biến cố giao của hai biến cố A và B, kí hiệu là A \cap B hay AB.

Hình vẽ minh họa

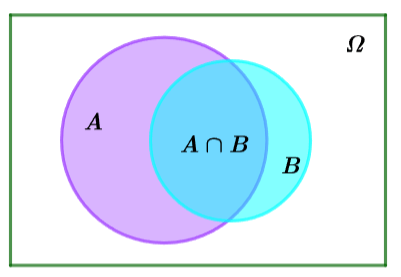
Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất

Chú ý: Biến cố D có thể phát biểu dưới dạng mệnh đề nêu sự kiện là “cả A và B cùng xảy ra”.

Ví dụ: Cho hai hộp đựng các viên bi. Hộp 1 chứa 4 viên bi xanh được đánh số theo thứ tự từ 1 đến 4. Hộp 2 chứa 3 viên bi đỏ được đánh số theo thứ tự từ 1 đến 3. Lấy ra ngẫu nhiên từ mỗi hộp 1 viên bi. Gọi A là biến cố: “Tổng các số ghi trên hai viên bi là 5“, B là biến cố “Tích các số trên hai viên bi là số chẵn. Hãy viết tập hợp mô tả biến cố AB.

Hướng dẫn giải

Ta có:

A = \left\{ (2;3),(3;2),(4;1) \right\}

B = \left\{ (1;2),(2;1),(2;2),(2;3),(3;2),(4;1),(4;2),(4;3) \right\}

AB = \left\{ (2;3),(3;2),(4;1) \right\}

3. Biến cố xung khắc

Cho hai biến cố A và B. Khi đó A,B là các tập con của không gian mẫu \Omega. Nếu A \cap B = \varnothing thì A và B gọi là hai biến cố xung khắc.

Chú ý: Hai biến cố A và B xung khắc khi và chỉ khi nếu biến cố này xảy ra thì biến cố kia không xảy ra.

Ví dụ: Một ban văn nghệ có 12 nữ và 8 nam. Chọn ngẫu nhiên 5 người để biểu diễn. Xét các biến cố sau:

M: “Trong 5 người được chọn, số nam lớn hơn 3”.

N: “Trong 5 người được chọn, số nữ nhỏ hơn 3”.

P: “Trong 5 người được chọn, số nam không vượt quá 3”.

Trong ba biến cố M, N, P hai biến cố nào xung khắc với nhau?

Hướng dẫn giải

Biến cố M và biến cố P là hai biến cố xung khắc với nhau.

Câu trắc nghiệm mã số: 44181

B. Biến cố độc lập

Cho hai biến cố A và B. Hai biến cố này được gọi là độc lập nếu việc xảy ra hay không xảy ra cả biến cố này không làm ảnh hưởng đến xác suất của biến cố kia.

Chú ý: Nếu A và B là hai biến cố độc lập thì mỗi cặp biến cố sau cũng độc lập: \left\{ \begin{matrix} A;\overline{B} \\ \overline{A};B \\ \overline{A};\overline{B} \\ \end{matrix} \right.

Ví dụ: Một hộp chứa 7 viên bi xanh và 8 viên bi đỏ, các viên bi đồng chất và cùng kích thước. Lấy một viên bi ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên 1 viên bi trong hộp, ghi lại màu của viên bi lấy ra và bỏ lại viên bi đó vào hộp. Xét các biến cố:

A: “Viên bi màu đỏ được lấy ở lần thứ nhất”.

B: “Viên bi màu xanh được lấy ra ở lần thứ hai”.

Hai biến cố A và B có độc lập không? Giải thích tại sao?

Hướng dẫn giải

Trước hết xác suất của biến cố B khi biến cố A xảy ra bằng \frac{7}{15}.

Xác suất của biến cố B khi biến cố A không xảy ra cũng bằng \frac{7}{15}.

Do đó việc xảy ra hay không xảy ra của biến cố A không làm ảnh hưởng đến xác suất xảy ra của biến cố B.

Mặt khác

Xác xuất của biến cố A bằng \frac{8}{15} không phụ thuộc vào việc xảy ra hay không xảy ra của biến cố B.

Vậy hai biến cố A và B độc lập.

Câu trắc nghiệm mã số: 44223

C. Các quy tắc tính xác suất

1. Công thức cộng xác suất

Cho hai biến cố A và B . Khi đó:

P(A \cup B) = P(A) + P(B) - P(A \cap B)

Hệ quả: Nếu hai biến cố A;B xung khắc thì P(A \cup B) = P(A) + P(B).

Ví dụ: Xét các biến cố A, B liên quan đến cùng một phép thử thỏa mãn P(A) = 0,4,P(B) = 0,5 và P(A \cup B) = 0,6. Hỏi hai biến cố A và B có xung khắc không? Vì sao?

Hướng dẫn giải

Ta có:

P(A \cup B) = P(A) + P(B) - P(A \cap B)

\Leftrightarrow P(A \cap B) = P(A) + P(B) - P(A \cup B)

\Leftrightarrow P(A \cap B) = 0,4 + 0,5 - 0,6 = 0,3

Suy ra A \cap B \neq \varnothing. Vậy hai biến cố A và B không xung khắc.

Câu trắc nghiệm mã số: 44237

2. Công thức nhân xác suất

Nếu hai biến cố A và B là độc lập thì P(A \cap B) = P(A).P(B).

Chú ý: Nếu P(A \cap B) \neq P(A).P(B) thì hai biến cố A và B không độc lập.

Ví dụ: Một hộp chứa 50 tấm thẻ cùng loại được đánh số từ 1 đến 50. Chọn ngẫu nhiên 1 thẻ từ hộp. Gọi A là biến cố “Số ghi trên thẻ được chọn chia hết cho 4”, B là biến cố “Số ghi trên thẻ được chọn chia hết cho 6”.

a) Bạn Minh nói AB là biến cố “Số ghi trên thẻ được chọn chia hết cho 24”. Minh nói vậy là đúng hay sai? Giải thích tại sao?

b) Hai biến cố A và B có độc lập hay không? Vì sao?

c) Hãy tìm một biến cố khác rỗng, xung khắc với cả hai biến cố A và biến cố B.

Hướng dẫn giải

a) Minh nói sai vì nếu lấy được thẻ ghi số 12 thì cả hai biến cố A và B đều xảy ra nhưng 12 không chia hết cho 24.

b) P(A) = \frac{C_{4}^{2}C_{4}^{2}}{C_{5}^{2}.C_{4}^{2}} = 0,6, P(B) = \frac{C_{5}^{2}C_{3}^{2}}{C_{5}^{2}.C_{4}^{2}} = 0,5, P(AB) = \frac{C_{4}^{2}C_{3}^{2}}{C_{5}^{2}.C_{4}^{2}} = 0,3

\Rightarrow P(AB) = P(A).P(B)

Vậy hai biến cố A và B độc lập.

c) Gọi C là biến cố “lấy ra từ mỗi hộp 1 viên bi xanh, 1 viên bi đỏ. Biến cố C xung khắc với cả hai biến cố A và B.

Câu trắc nghiệm mã số: 44243

D. Tính xác suất của biến cố trong một số bài toán đơn giản

1. Tính xác suất của biến cố bằng phương pháp tổ hợp

Ví dụ: Chọn ngẫu nhiên 4 viên bi từ hộp chứa 4 viên bi xanh, 5 viên bi đỏ và 3 viên bi vàng. Tính xác suất của các biến cố:

a) Cả 4 viên bi lấy ra cùng màu.

b) Trong 4 viên bi lấy ra có ít nhất 3 viên bi xanh.

Hướng dẫn giải

a) Gọi A là biến cố “Cả 4 viên bi lấy ra có cùng màu xanh”, B là biến cố “Cả 4 viên bi lấy ra cùng màu đỏ”.

Vì chỉ có 3 viên bi màu vàng nên A \cup B là biến cố “Cả 4 viên bi lấy ra có cùng màu”.

Do A và B là hai biến cố xung khắc nên

P(A \cup B) = P(A) + P(B)

= \frac{C_{4}^{4}}{C_{12}^{4}} + \frac{C_{5}^{4}}{C_{12}^{4}} = \frac{2}{165}

b) Gọi C là biến cố “Có 3 viên bi xanh trong 4 viên lấy ra”. Khi đó A \cup C là biến cố “Có ít nhất 3 viên bi xanh trong 4 viên bi lấy ra”. Do A và C là hai biến cố xung khắc nên:

P(A \cup C) = P(A) + P(C)

= \frac{C_{4}^{4}}{C_{12}^{4}} + \frac{C_{4}^{3}.C_{8}^{1}}{C_{12}^{4}} = \frac{1}{15}

2. Tính xác suất của biến cố bằng cách sử dụng sơ đồ hình cây

Ví dụ: Một hộp chứa 9 tấm thẻ gồm 4 tấm thẻ màu xanh được đánh số từ 1 đến 4, 3 tấm thẻ màu vàng đánh số từ 1 đến 3 và 2 tấm thử màu đỏ đánh số từ 1 đến 2. Lấy ngẫu nhiên 2 tấm thẻ trong hộp. Tính xác suất để hai tấm thẻ lấy được vừa khác màu vừa khác số.

Hướng dẫn giải

Mỗi cách lấy ngẫu nhiên hai tấm thể từ hộp 9 tấm thẻ cho ta một tổ hợp chập 2 của 9 phần tử.

Do đó không gian mẫu là n(\Omega) = C_{9}^{2} = 36 .

Xét biến cố A: “Lấy được 2 tấm thẻ vừa khác màu vừa khác số”.

Sơ đồ hình cây biểu thị khả năng thuận lợi cho biến cố A như sau:

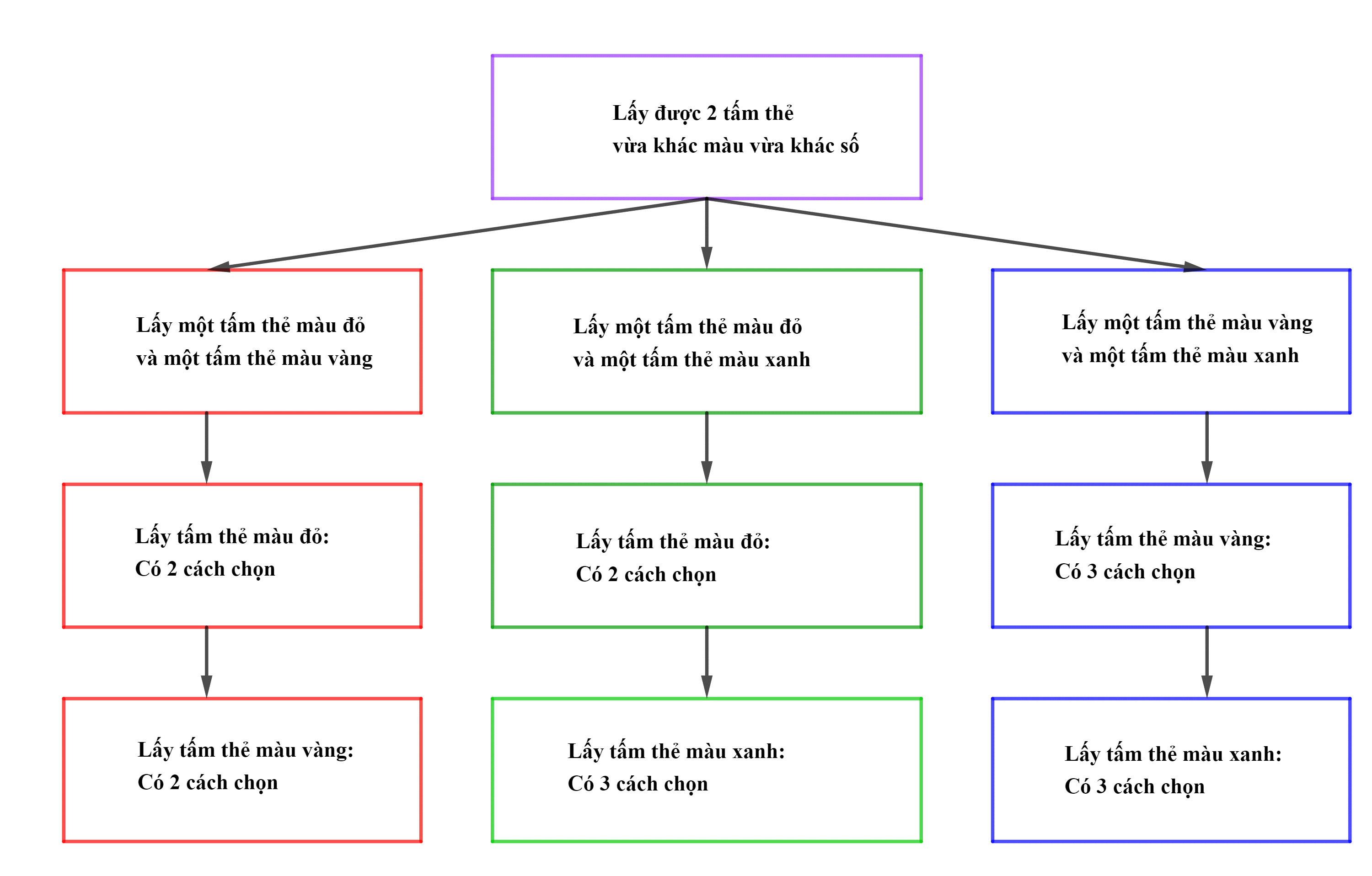
Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất

Suy ra n(A) = 2.2 + 2.3 + 3.3 = 19

P(A) = \frac{n(A)}{n(\Omega)} = \frac{19}{36}.

  • 19 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CD