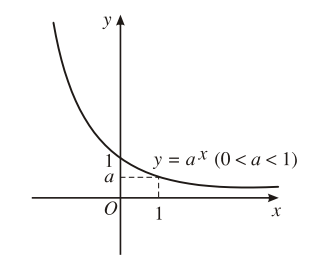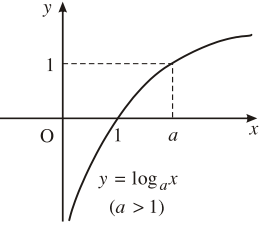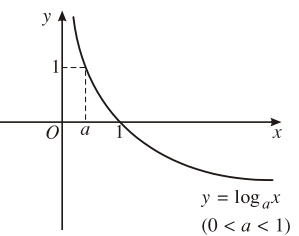Hàm số mũ. Hàm số lôgarit Cánh Diều
A. Hàm số mũ
1. Định nghĩa
Cho số thực dương ![]() . Hàm số
. Hàm số ![]() được gọi là hàm số mũ cơ số
được gọi là hàm số mũ cơ số ![]() .
.
Ví dụ: Tìm tập xác định của hàm số: ![]()
Hướng dẫn giải
Điều kiện xác định của hàm số là ![]()
Vậy tập xác định của hàm số là ![]() .
.
2. Đồ thị và tính chất
|
|
|
|
| 1. Tập xác định |
|
|
| 2. Sự biến thiên | Đồng biến trên |
Nghịch biến trên |
| 3. Sự liên tục | ||
| 4. Giới hạn đặc biệt |  |
 |
| 5. Bảng biến thiên | 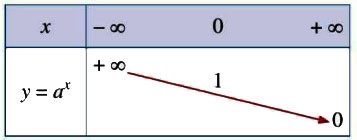 |
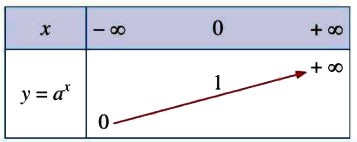 |
|
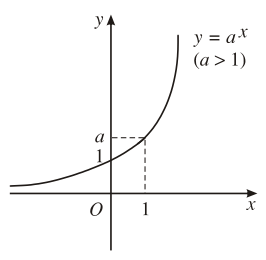
6. Đồ thị hàm số |
Đồ thị luôn đi qua các điểm |
Đồ thị luôn đi qua các điểm |
Ví dụ: Lập bảng biến thiên, vẽ đồ thị hàm số: ![]() .
.
Hướng dẫn giải
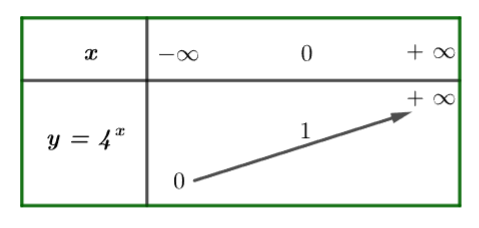
Vì hàm số ![]() có cơ số
có cơ số ![]() nên ta có bảng biến thiên như sau:
nên ta có bảng biến thiên như sau:
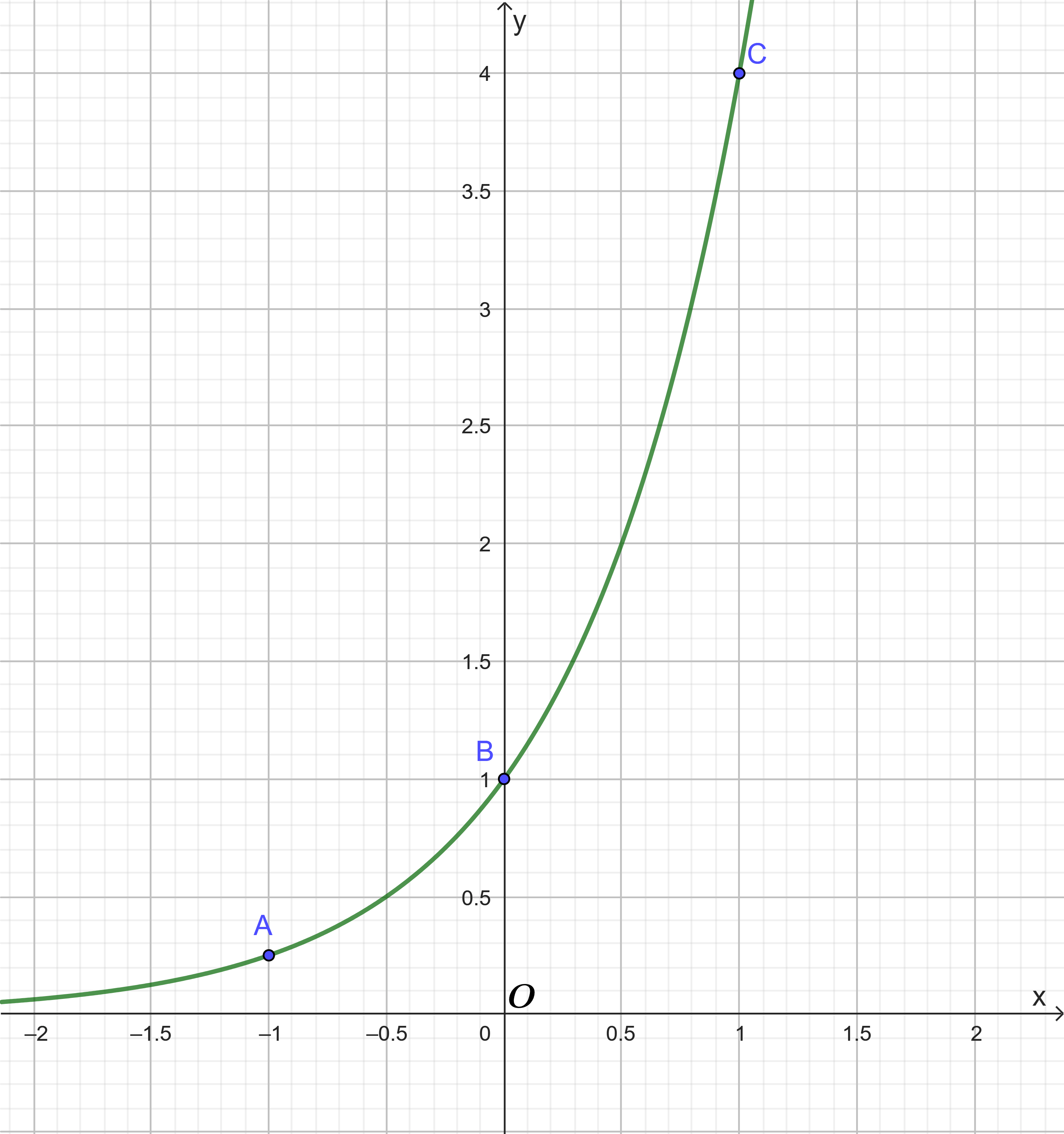
Đồ thị hàm số ![]() là một đường cong nét liền đi qua các điểm
là một đường cong nét liền đi qua các điểm ![]() như sau:
như sau:
B. Hàm số lôgari
1. Định nghĩa
Cho ![]() là số thực dương và
là số thực dương và ![]() . Hàm số
. Hàm số ![]() được gọi là hàm số lôgarit cơ số
được gọi là hàm số lôgarit cơ số ![]() .
.
Ví dụ: Tìm tập xác định của hàm số:
| a) |
b) |
Hướng dẫn giải
a) Điều kiện xác định của hàm số là
![]()
![]()
Vậy tập xác định của hàm số là ![]()
b) Điều kiện xác định của hàm số là
![]()
![]() luôn đúng với
luôn đúng với ![]()
Vậy tập xác định của hàm số là ![]()
2. Đồ thị và tính chất
|
|
|
|
| 1. Tập xác định |
|
|
| 2. Sự biến thiên | Đồng biến trên |
Nghịch biến trên |
| 3. Sự liên tục | ||
| 4. Giới hạn đặc biệt |
|
|
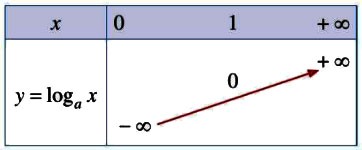
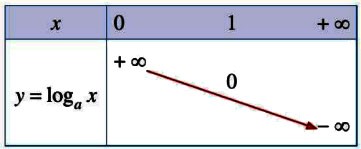
| 5. Bảng biến thiên |
|
|
|
5. Đồ thị hàm số |
Đi qua các điểm |
Đi qua các điểm |
Ví dụ: Lập bảng biến thiên, vẽ đồ thị hàm số: ![]() .
.
Hướng dẫn giải
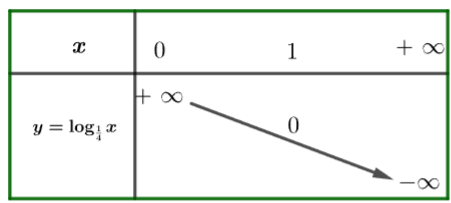
Vì hàm số ![]() có cơ số
có cơ số ![]() nên ta có bảng biến thiên như sau:
nên ta có bảng biến thiên như sau:
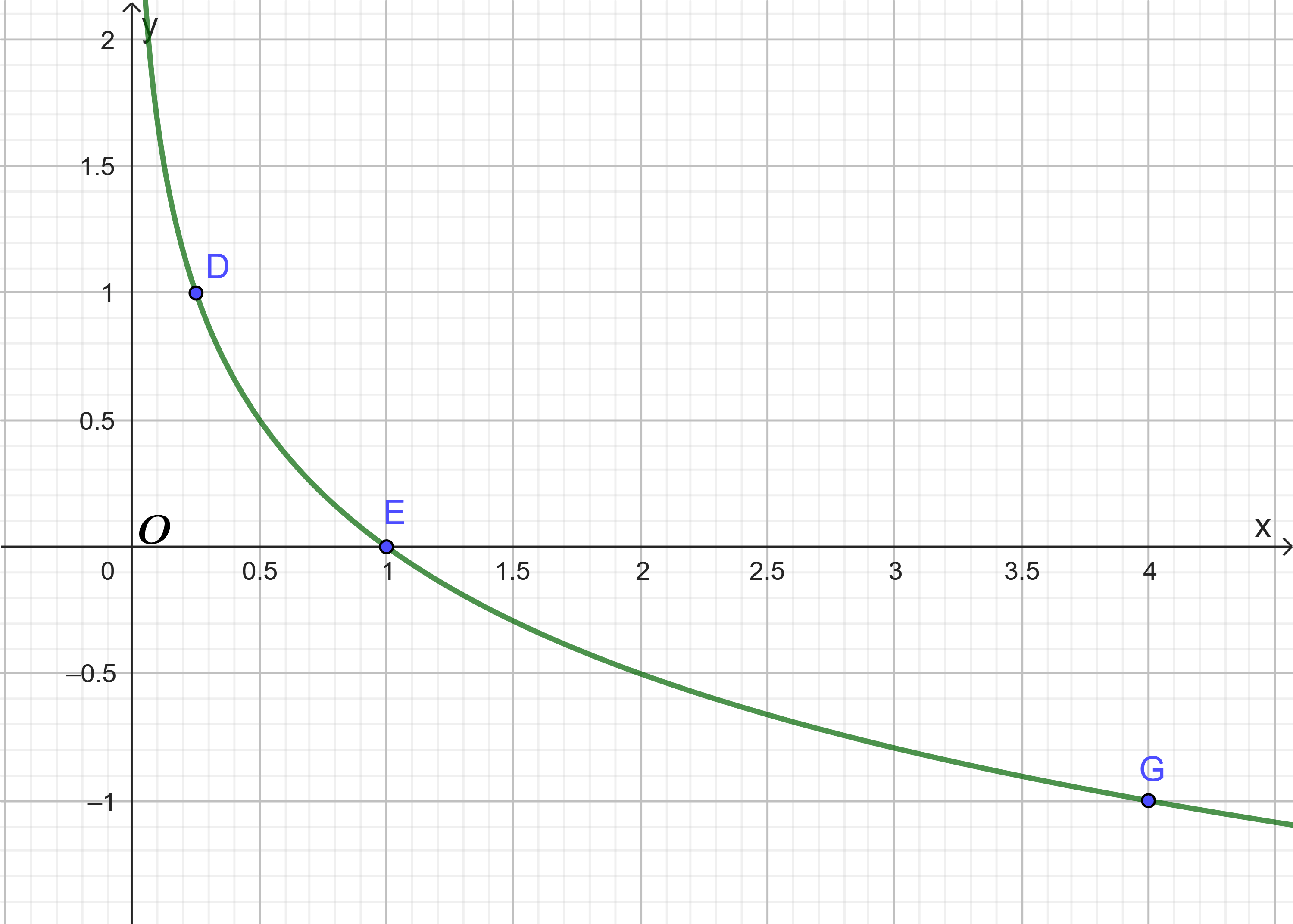
Đồ thị hàm số ![]() là một đường cong liền nét đi qua các điểm
là một đường cong liền nét đi qua các điểm ![]() như sau:
như sau:
Ví dụ: Tìm tất cả các giá trị của tham số m để hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() .
.
Hướng dẫn giải
Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() khi và chỉ khi
khi và chỉ khi
![]()
![]()
Nội dung cùng chủ đề
-
Đề khảo sát chất lượng
-
Chương 1: Hàm số lượng giác và phương trình lượng giác
-
Chương 2: Dãy số. Cấp số cộng và cấp số nhân
-
Chương 3: Giới hạn. Hàm số liên tục
-
Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
Chương 5: Một số yếu tố thống kê và xác suất
-
Chương 6: Hàm số mũ và hàm số lôgarit
-
Chương 7: Đạo hàm
-
Chương 8: Quan hệ vuông góc trong không gian. Phép chiếu vuông góc
-
Đề thi Học kì