Lớp 11 Toán 11 - Cánh Diều

Hình lăng trụ và hình hộp Cánh Diều

A. Hình lăng trụ

1. Định nghĩa hình lăng trụ

Hình gồm hai đa giác A_{1}A_{2}...A_{n} ; A_{1}'A_{2}'...A_{n}' và các hình bình hành A_{1}A_{2}A_{2}'A_{1}';A_{2}A_{3}A_{3}'A_{2}'; …; A_{n}A_{1}A_{1}'A_{n}' được gọi là hình lăng trụ.

Kí hiệu là A_{1}A_{2}...A_{n}.A_{1}'A_{2}'...A_{n}'

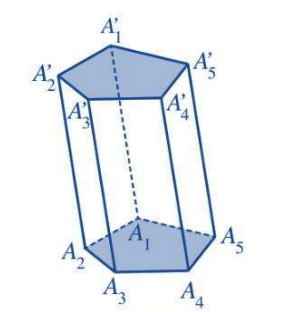
Hình lăng trụ và hình hộp Cánh Diều

Chú ý: Nếu đáy của hình lăng trụ là một tam giác, tứ giác, ngũ giác, … thì lăng trụ ấy tương ứng gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác, …

Đặc điểm của hình lăng trụ

Trong hình lăng trụ A_{1}A_{2}...A_{n}.A_{1}'A_{2}'...A_{n}' có:

  • Hai đa giác A_{1}A_{2}...A_{n} và A_{1}'A_{2}'...A_{n}' gọi là hai mặt đáy.
  • Các hình bình hành A_{1}A_{2}A_{2}'A_{1}';A_{2}A_{3}A_{3}'A_{2}'; …; A_{n}A_{1}A_{1}'A_{n}' gọi là các mặt bên.
  • Các cạnh của hai mặt đáy gọi là các cạnh đáy.
  • Các đoạn thẳng A_{1}A_{1}';A_{2}A_{2}';A_{3}A_{3}';...;A_{n}A_{n}' gọi là các cạnh bên.
  • Các đỉnh của hai mặt đáy gọi là các đỉnh của hình lăng trụ.

2. Tính chất của hình lăng trụ

  • Các cạnh bên của hình lăng trụ song song và bằng nhau.
  • Các mặt bên của hình lăng trụ là hình bình hành.
  • Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau.

Ví dụ: Cho hình lăng trụ ABC.A'B'C'. Gọi trọng tâm các tam giác ABC,ACC',A'B'C' lần lượt là I,J,K. Tìm mặt phẳng song song với mặt phẳng (IJK).

Hướng dẫn giải

Hình vẽ minh họa

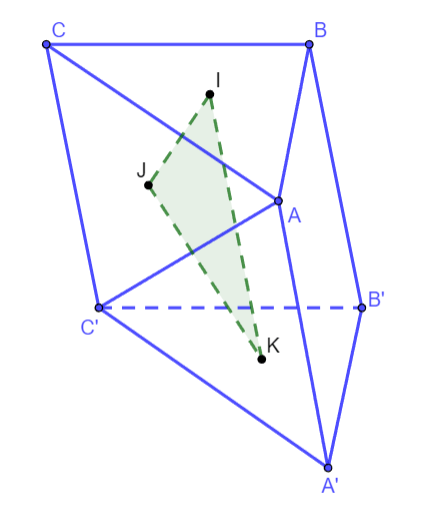
Hình lăng trụ và hình hộp Cánh Diều

Theo bài ra ta có:

Các điểm I,J,K lần lượt là trọng tâm các tam giác ABC,ACC',A'B'C'.

\Rightarrow \frac{AI}{AM} = \frac{AJ}{AN} = \frac{2}{3} \Rightarrow IJ//MN.

\Rightarrow IJ//(BCC'B')

Chứng minh tương tự IK//(BCC'B') \Rightarrow (IJK)//(BCC'B')

\Rightarrow (IJK)//(BC'B')

Câu trắc nghiệm mã số: 35033

B. Hình hộp

1. Định nghĩa hình hộp

Hình hộp là hình lăng trụ có đáy là hình bình hành.

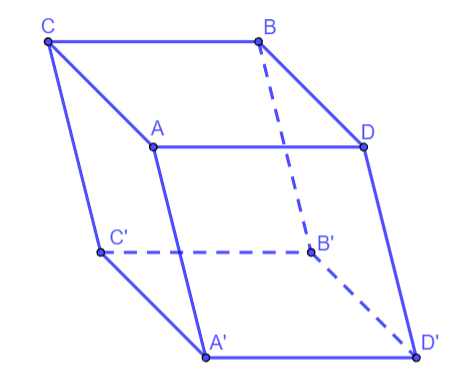
Hình lăng trụ và hình hộp Cánh Diều

Câu trắc nghiệm mã số: 35552

Một số định nghĩa trong hình hộp

  • Hai mặt không có đỉnh chung gọi là hai mặt đối diện.
  • Hai cạnh song song không nằm trong một mặt là hai cạnh đối diện.
  • Hai đỉnh không thuộc cùng một mặt là hai đỉnh đối diện.
  • Đoạn thẳng nối hai đỉnh đối diện là đường chéo.

2. Tính chất của hình hộp

  • Các mặt của hình hộp là các hình bình hành.
  • Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.

Nhận xét: Ta có thể coi hai mặt đối diện bất kì của một hình hộp là hai mặt đáy của nó.

Ví dụ: Cho hình hộp ABCD.A'B'C'D' . Lấy M \in AD,N \in CC' sao cho 2AM = AD và 2CN = CC' . Mặt phẳng (\alpha) chứa đường thẳng MN và song song với (ACB') . Xác định các giao tuyến của (\alpha) với các mặt của hình hộp. Cho biết hình tạo bởi các giao tuyến đó là hình gì?

Hướng dẫn giải

Hình vẽ minh họa

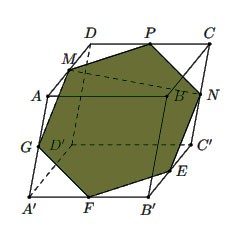
Hình lăng trụ và hình hộp Cánh Diều

Giao tuyến của (\alpha) với mặt phẳng (ABCD) là đường thẳng qua M và song song với AC, đường thẳng này cắt CD tại P là trung điểm CD.

Giao tuyến của (\alpha) với mặt phẳng (BCC’B’) là đường thẳng qua N và song song với B’C, đường thẳng này cắt B’C’ tại E là trung điểm B’C’.

Giao tuyến của (\alpha) với mặt phẳng (A’B’C’D’) là đường thẳng qua E và song song với A’C’, đường thẳng này cắt A’B’ tại F là trung điểm A’B’.

Giao tuyến của (\alpha) với mặt phẳng (ABB’A’) là đường thẳng qua F và song song với AB’, đường thẳng này cắt AA’ tại G là trung điểm AA’.

=> Hình lục giác MPNEFG là hình tạo bởi các giao tuyến của (\alpha) với các mặt của hình hộp.

Câu trắc nghiệm mã số: 35049
  • 37 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CD