Đường thẳng và mặt phẳng trong không gian Cánh Diều

A. Khái niệm mở đầu

1. Mặt phẳng

Mặt gương, mặt bàn, mặt bảng, mặt nước lúc tĩnh lặng, … là một số ví dụ về một phần của mặt phẳng. Mặt phẳng không có bề dày và không có giới hạn.

Chú ý:

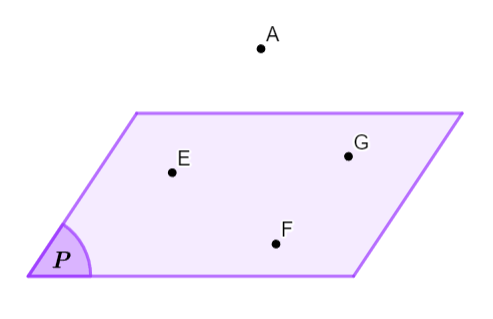
Để biểu diễn mặt phẳng ta thường dùng một hình bình hành và viết tên của mặt phẳng vào một góc của hình.
Để kí hiệu mặt phẳng ta dùng chữ cái in hoa hoặc chữ cái Hy Lạp đặt trong dấu ( ) ví dụ: mặt phẳng (P), mặt phẳng (α), …

Minh họa

Đường thẳng và mặt phẳng trong không gian Cánh Diều

2. Điểm thuộc mặt phẳng

Điểm M thuộc mặt phẳng (P) kí hiệu là $M \in (P)$ .

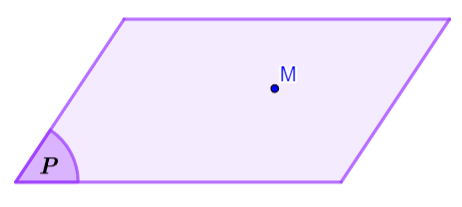
Đường thẳng và mặt phẳng trong không gian Cánh Diều

Điểm N không thuộc mặt phẳng (P) kí hiệu là $N \notin (P)$ .

Đường thẳng và mặt phẳng trong không gian Cánh Diều

Chú ý: Nếu $M \in (P)$ ta còn nói M nằm trên (P) hoặc (P) chứa M, hoặc (P) đi qua N.

3. Hình biểu diễn của một hình trong không gian

a) Định nghĩa

Hình được vẽ trong mặt phẳng để giúp ta hình dung được về một hình trong không gian được gọi là hình biểu diễn của hình trong không gian đó.

b) Quy tắc vẽ hình biểu diễn của một hình trong không gian

Đường thẳng được biểu diễn bởi đường thẳng. Đoạn thẳng được biểu diễn bởi đoạn thẳng.
Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi hai đường thẳng song song (hoặc cắt nhau).
Hình biểu diễn giữ nguyên tính liên thuộc giữa điểm với đường thẳng hoặc với đoạn thẳng.
Những đường nhìn thấy được vẽ bằng nét liền, những đường không nhìn thấy được vẽ bằng nét đứt.

Ví dụ minh họa

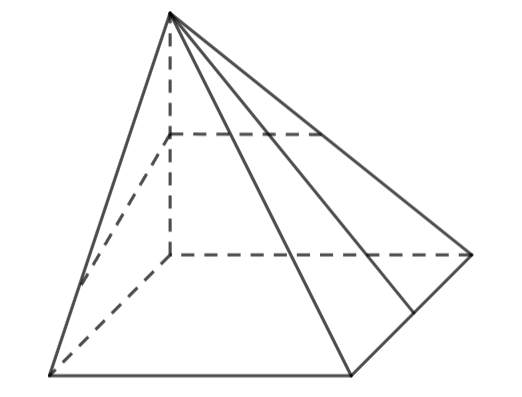
Đường thẳng và mặt phẳng trong không gian Cánh Diều

B. Các tính chất thừa nhận của hình học không gian

Tính chất 1

Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

Tính chất 2

Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

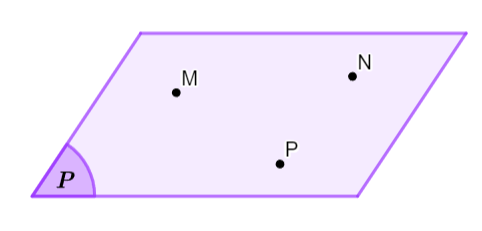
Đường thẳng và mặt phẳng trong không gian Cánh Diều

Tính chất 3

Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.

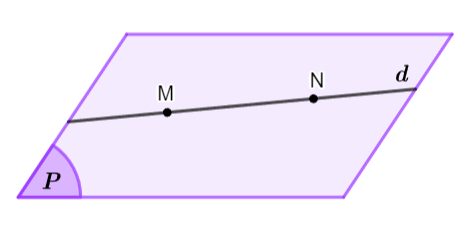
Đường thẳng và mặt phẳng trong không gian Cánh Diều

Tính chất 4

Tồn tại bốn điểm không nằm trên một mặt phẳng.

Đường thẳng và mặt phẳng trong không gian Cánh Diều

Tính chất 5

Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng nó có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

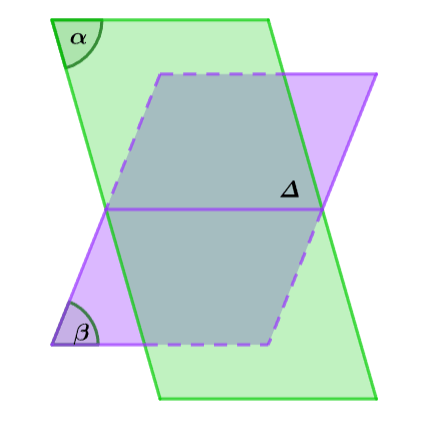
Đường thẳng và mặt phẳng trong không gian Cánh Diều

Nhận xét:

Có thể xác định giao tuyến của hai mặt phẳng bằng cách đi tìm hai điểm chung của chúng. Đường thẳng đi qua hai điểm chung đó được gọi là giao tuyến.
Để tìm giao điểm của đường thẳng a và mặt phẳng (P) (giả thiết a cắt (P)) ta có thể thực hiện như sau:
Chọn một đường thẳng b thích hợp trong mặt phẳng (P) và tìm giao điểm M của hai đường thẳng a và b. Khi đó M là giao điểm cần tìm.

Ví dụ: Cho bốn điểm $A, B, C, D$ không đồng phẳng. Lấy điểm $M$ bất kì bên trong tam giác $ABD$ và điểm $N$ nằm trong tam giác $ACD$ . Hãy xác định giao tuyến của hai mặt phẳng:

a) $(AMN), (BCD)$

b) $(DMN), (ABC)$

Hướng dẫn giải

Hình vẽ minh họa

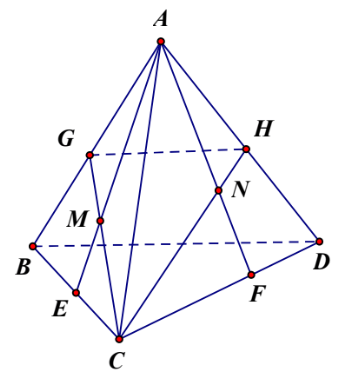
Đường thẳng và mặt phẳng trong không gian Cánh Diều

a) Gọi $E = AM \cap BD$ , $F = AN \cap CD$ .

Ta có:

$E \in AM \Rightarrow E \in (AMN)$

$F \in AN \Rightarrow F \in (AMN)$

$\Rightarrow EF \in (AMN)(*)$

Lại có:

$E \in BD \Rightarrow E \in (BCD)$

$F \in CD \Rightarrow F \in (BCD)$

$\Rightarrow EF \in (BCD)(**)$

Từ (*) và (**) suy ra $E \in AM \Rightarrow E \in (AMN)$

$F \in AN \Rightarrow F \in (AMN)$

$\Rightarrow EF \in (AMN) \cap (BCD)$

b) Gọi $G = DM \cap AB$ và $H = DN \cap AC$

Chứng minh tương tự câu a ta có:

$\Rightarrow GH \in (DMN) \cap (ABC)$

Câu trắc nghiệm mã số: 35535,35532

Tính chất 6

Trên mỗi mặt phẳng của không gian, các kết quả đã biết của hình học phẳng đều đúng.

C. Một số cách xác định mặt phẳng

Định lí 1

Cho điểm A không thuộc đường thẳng a. Khi đó, qua điểm A và đường thẳng a có một và chỉ một mặt phẳng. Kí hiệu: $mp(A, d)$ hoặc $(A, d)$ .

Định lí 2

Cho hai đường thẳng a và b cắt nhau. Khi đó qua a và b có một và chỉ một mặt phẳng. Kí hiệu $mp(a; b)$ .

Nhận xét: Một mặt phẳng hoàn toàn được xác định bằng một trong ba cách sau:

Đi qua ba điểm không thẳng hàng.
Đi qua một đường thẳng và một điểm nằm ngoài đường thẳng.
Đi qua hai đường thẳng cắt nhau.

D. Hình chóp và hình tứ diện

1. Hình chóp

Trong mặt phẳng (P) cho đa giác $A_{1}A_{2}...A_{n};(n \geq 3)$ . Lấy điểm S nằm ngoài (P). Nối S với các đỉnh $A_{1};A_{2};...;A_{n}$ ta được $n$ tam giác $SA_{1}A_{2};SA_{2}A_{3};...;SA_{n}A_{1}$ . Hình gồm đa giác $A_{1}A_{2}...A_{n}$ và n tam giác $SA_{1}A_{2};SA_{2}A_{3};...;SA_{n}A_{1}$ được gọi là hình chóp. Kí hiệu $S.A_{1}A_{2}...A_{n}$ .

Minh hoạ

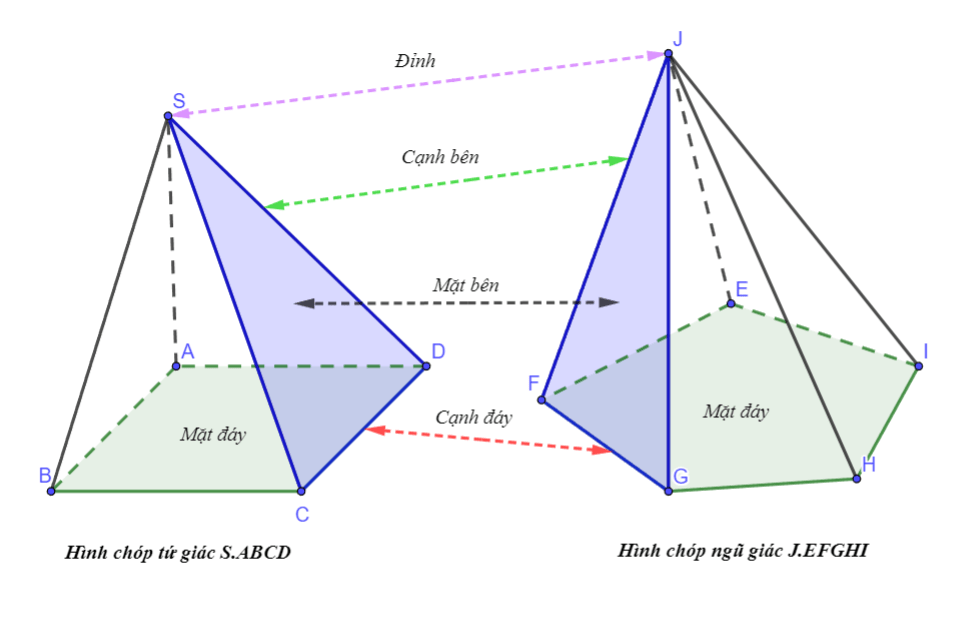
Đường thẳng và mặt phẳng trong không gian Cánh Diều

Đặc điểm của hình chóp

Điểm S được gọi là đỉnh hình chóp.
Đa giác $A_{1}A_{2}...A_{n}$ là mặt đáy.
Các cạnh của mặt đáy gọi là các cạnh đáy, các đoạn thẳng nối đỉnh S với các đỉnh của đa giác đáy gọi là các cạnh bên.
Các tam giác $SA_{1}A_{2};SA_{2}A_{3};...;SA_{n}A_{1}$ gọi là các mặt bên.

Nhận xét: Nếu đáy của hình chóp là một tam giác, tứ giác, ngũ giác, … thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác, …

2. Hình tứ diện

Cho bốn điểm $A, B, C, D$ không cùng nằm trên một mặt phẳng. Hình gồm bốn tam giác $ABC, ACD, ABD, BCD$ gọi là hình tứ diện (hay tứ diện). Kí hiệu là $ABCD$ .

Minh họa

Đường thẳng và mặt phẳng trong không gian Cánh Diều

Đặc điểm của tứ diện

Xét tứ diện $ABCD$
Các điểm $A, B, C, D$ gọi là các đỉnh.
Các đoạn thẳng $AB, BC, CD, DA, CA, BD$ được gọi là các cạnh.
Hai cạnh không có điểm chung gọi là hai cạnh đối diện.
Các tam giác $ABC, ACD, ABD, BCD$ là các mặt.
Đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.

Chú ý:

Hình tứ diện có các mặt là tam giác đều là hình tứ diện đều
Mỗi hình chóp tam giác là một hình tứ diện. Nếu ta quy định rõ ràng đỉnh và mặt đáy trong một hình tứ diện thì hình tứ diện đó trở thành hình chóp tam giác.
Để chứng minh ba điểm thẳng hàng ta có thể chỉ ra ba điểm đó cùng thuộc hai mặt phẳng phân biệt.

Ví dụ: Cho tứ diện $ABCD$ . Gọi $M, N$ lần lượt là trung điểm của $AB$ và $CD$ . Mặt phẳng $(α)$ qua $MN$ cắt $AD, BC$ lần lượt tại $P$ và $Q$ . Biết $MP$ cắt $NQ$ tại $I$ . Chứng minh ba điểm $I, B, D$ thẳng hàng.