Lớp 11 Toán 11 - Cánh Diều

Ôn tập chương 8 Quan hệ vuông góc trong không gian. Phép chiếu vuông góc

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Khoảng cách giữa hai đường thẳng BC và AB’

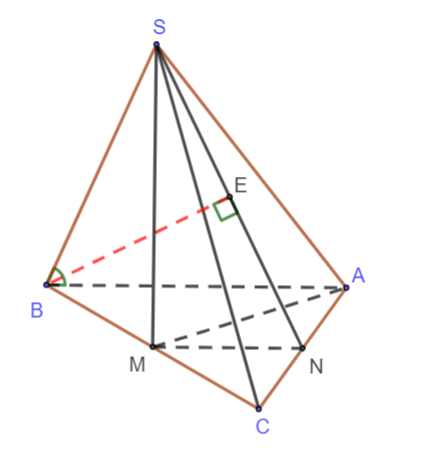
    Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Khoảng cách giữa hai đường thẳng BC và AB’ bằng:

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có BC // B’C’ => BC // (AB’C’)

    => d(BC, AB’) = d(BC, (AB’C’)) = d(B, (AB’C’)) = d(A’ ,(AB’C’))

    Gọi I và H lần lượt là hình chiếu vuông góc của A’ trên B’C’ và AI

    Ta có: B’C’⊥ A’I và B’C’⊥ A’A nên B’C’⊥ (A’AI) => B’C’⊥ A’H

    Mà AI ⊥ A’H

    => (AB’C’) ⊥ A’H.

    Khi đó:

    d\left( A';(AB'C') ight) =A'H = \frac{AA'.A'I}{\sqrt{AA'^{2} +A'I^{2}}}

    =\dfrac{a.\dfrac{a\sqrt{3}}{2}}{\sqrt{a^{2} + \left( \dfrac{a\sqrt{3}}{2}ight)^{2}}} = \dfrac{a\sqrt{21}}{7}

    Vậy khoảng cách cần tìm là \frac{a\sqrt{21}}{7}

  • Câu 2: Vận dụng cao
    Xác định thể tích khối lăng trụ

    Cho khối lăng trụ ABC.A'B'C', hình chiếu vuông góc của điểm A lên mặt phẳng (A'B'C') là trung điểm M của BC. Biết A'M = \frac{2a\sqrt{3}}{3};d(C;BB') = 2a;d(A;BB') = a;d(A;CC') = a\sqrt{3}. Thể tích của khối lăng trụ là:

    Hướng dẫn:

    Hình vẽ minh họa:

    Cắt lăng trụ bởi một mặt phẳng qua A’ vuông góc với AA’ ta được một thiết diện là tam giác A'B_{1}C_{1} có các cạnh:

    A'B_{1} = a;A'C_{1} = a\sqrt{3};B_{1}C_{1} = 2a

    Suy ra tam giác A'B_{1}C_{1} vuông tại A’ và trung tuyến A’H của tam giác đó bằng a

    Gọi giao điểm của AM và A’H là T

    Ta có:

    A'M = \frac{2a\sqrt{3}}{3};A'H = a

    \Rightarrow MH = \frac{a}{\sqrt{3}} \Rightarrow \widehat{MA'H} = 30^{0} \Rightarrow \widehat{MA'A} = 60^{0}

    \Rightarrow AA' = \frac{A'M}{\cos\widehat{MA'A}} = \frac{4a}{\sqrt{3}}

    \Rightarrow V_{ABC.A'B'C'} = V_{A'B_{1}C_{1}.ABC} = AA'.S_{A'B_{1}C_{1}} = 2a^{3}

  • Câu 3: Thông hiểu
    Xác định thể tích V của khối chóp

    Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a. Biết \left( (SAB);(ABCD) ight) = 90^{0} và tam giác SAB đều. Xác định thể tích hình chóp S.ABCD?

    Hướng dẫn:

    Hình vẽ minh họa

    Gọi H là trung điểm của AB

    Tam giác SAB đều nên SH\bot AB

    Ta có: \left\{ \begin{matrix} SH\bot AB \\ (SAB)\bot(ABCD) \\ SH \subset (SAB) \\ AB = (SAB) \cap (ABCD) \\ \end{matrix} ight.\ \Rightarrow SH\bot(ABCD)

    Vậy SH là đường cao của hình chóp

    Xét tam giác AHS vuông tại H ta có:

    SH = \sqrt{SA^{2} - AH^{2}} = \sqrt{a^{2} - \left( \frac{a}{2} ight)^{2}} = \frac{a\sqrt{3}}{2}

    Thể tích khối chóp là: V = \frac{1}{3}B.h = \frac{1}{3}.a^{2}.\frac{a\sqrt{3}}{2} = \frac{a^{3}\sqrt{3}}{6}

  • Câu 4: Thông hiểu
    Tính khoảng cách d từ B đến mặt phẳng (SAC)

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a, AC=a\sqrt{3}. Tam giác SBC đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách d từ B đến mặt phẳng (SAC). 

    Hướng dẫn:

    Hình vẽ minh họa:

    Tính khoảng cách d từ B đến mặt phẳng (SAC)

    Gọi M là trung điểm của BC

    => SH \bot BC \Rightarrow SH \bot \left( {ABC} ight)

    Gọi N là trung điểm của AC

    => MN \bot AC

    Kẻ ME \bot SN,\left( {E \in SN} ight)

     \begin{matrix} d\left( {B,\left( {SAC} ight)} ight) = 2d\left( {M;\left( {SAC} ight)} ight) \hfill \\ = 2ME = 2.\dfrac{{SM.MN}}{{\sqrt {S{M^2} + M{N^2}} }} = \dfrac{{2a\sqrt {39} }}{{13}} \hfill \\ \end{matrix}

  • Câu 5: Thông hiểu
    Xác định góc giữa hai mặt phẳng

    Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A và SA ⊥ (ABC). M là trung điểm của BC. Hãy xác định góc giữa hai mặt phẳng (ABC) và (SBC).

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có: Giao tuyến của hai mặt phẳng (SBC) và (ABC) là BC. (1)

    Ta có: SA ⊥ (ABC), mà đường thẳng BC nằm trong (ABC) => SA ⊥ BC.

    Do tam giác ABC cân tại A và M là trung điểm BC => BC ⊥ AM tại M.

    Như vậy: \left\{ \begin{matrix} BC\bot MA \subset (SAM) \\ BC\bot SA \subset (SAM) \\ MA\ \cap \ SA = A \\ \end{matrix} ight.\ \Rightarrow (SAM)\bot BC.\ (2)

    Lại có: \left\{ \begin{matrix} (SMA) \cap (ABC) = MA \\ (SMA) \cap (SBC) = MS \\ \end{matrix} ight.

    Từ (1), (2), (3) => \alpha = \widehat{SMA}

  • Câu 6: Nhận biết
    Chọn mệnh đề đúng

    Cho hình chóp S.ABCD có đáy là hình vuông ABCD, SA vuông góc với đáy. Kẻ AH vuông góc với SB (H ∈ SB). Chọn mệnh đề đúng.

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có:

    SA ⊥ BC

    AB ⊥ BC

    => BC ⊥ (SAB) => BC ⊥ AH

    Mà AH ⊥ SB nên AH ⊥ (SBC) => AH ⊥ SC

  • Câu 7: Thông hiểu
    Tính độ dài MN

    Cho tứ diện ABCD;AC = 6a;BD = 8a. Gọi trung điểm của AD,BC lần lượt là M,N. Biết AC\bot DB. Độ dài đoạn thẳng MN là:

    Hướng dẫn:

    Hình vẽ minh họa

    Gọi P là trung điểm của CD. Khi đó \left\{ \begin{matrix}MP = \dfrac{1}{2}AC = 3a \\NP = \dfrac{1}{2}BD = 4a \\\end{matrix} ight.

    Lại có \left\{ \begin{matrix} NP//BD;MP//AC \\ AC\bot BD \\ \end{matrix} ight.\ \Rightarrow MP\bot NP hay tam giác MNP vuông tại P

    Theo định lí Pythagore ta có:

    MN = \sqrt{NP^{2} + MP^{2}} = 5a

  • Câu 8: Thông hiểu
    Chọn mệnh đề đúng

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \widehat{ABC} = 60^{0} , tam giác SBC là tam giác đều có bằng cạnh 2a và nằm trong mặt phẳng vuông với đáy. Gọi \varphi là góc giữa hai mặt phẳng (SAC) và (ABC). Mệnh đề nào sau đây đúng?

    Hướng dẫn:

    Hình vẽ minh họa:

    Gọi H là trung điểm của BC, suy ra SH ⊥ BC

    => SH ⊥ (ABC).

    Gọi K là trung điểm AC=> HK // AB nên HK ⊥ AC.

    Ta có:

    \left\{ \begin{matrix} AC\bot HK \\ AC\bot SH \\ \end{matrix} ight.\ \Rightarrow AC\bot(SHK) \Rightarrow AC\bot SK.

    => ((SAC), (ABC)) = (SK, HK) = \widehat{SHK}

    Xét tam giác vuông ABC ta có:

    \begin{matrix}AB = BC.cos\widehat{ABC} = a \hfill\\\Rightarrow HK = \dfrac{1}{2}AB = \dfrac{a}{2} \hfill\\\end{matrix}

    Xét tam giác vuông SHK ta có: \tan\widehat{SHK} = \frac{SH}{HK} = 2\sqrt{3}

  • Câu 9: Thông hiểu
    Tính thể tích khối chóp

    Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Góc tạo bởi cạnh bên SB và mặt phẳng đáy bằng 60^{0}. Thể tích khối chóp là:

    Hướng dẫn:

    Hình vẽ minh họa

    Gọi H là tâm của tam giác đều ABC

    Khi đó SH\bot(ABC);BH = \frac{a\sqrt{3}}{3}

    Theo bài ra ta có:

    \left( SB;(ABC) ight) = \widehat{SBH} = 60^{0}

    Tam giác SBH vuông tại H có: SH = BH.tan60^{0} = \frac{a\sqrt{3}}{3}.\sqrt{3} = a

    \Rightarrow V_{S.ABC} = \frac{1}{3}.SO.S_{ABC} = \frac{1}{3}.a.\frac{a^{2}\sqrt{3}}{4} = \frac{\sqrt{3}a^{3}}{12}

  • Câu 10: Thông hiểu
    Tính tan góc giữa đường thẳng và mặt phẳng

    Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a. Biết góc giữa hai mặt phẳng (SAB) và mặt phẳng (ABCD) bằng 90^{0}, SA = SB. Tính tan góc giữa SC và mặt phẳng (ABCD), biết thể tích khối chóp S.ABCD bằng \frac{4a^{3}}{3}?

    Hướng dẫn:

    Hình vẽ minh họa

    Kẻ SH\bot AB , gọi \alpha = \left( SC;(ABCD) ight)

    Ta có: \left\{ \begin{matrix} (SAB)\bot(ABCD) \\ (SAB) \cap (ABCD) = AB \\ SH \subset (SAB) \\ \end{matrix} ight.\ \Rightarrow SH\bot(ABCD)

    \Rightarrow \alpha = \widehat{SCH}

    Lại có: V_{S.ABCD} = \frac{1}{3}SH.S_{ABCD} = \frac{4a^{3}}{3} \Rightarrow SH = a

    Do tam giác SAB cân tại S nên H là trung điểm của AB

    \Rightarrow HC = \sqrt{BH^{2} + BC^{2}} = a\sqrt{5}

    \Rightarrow \tan\alpha = \tan\widehat{SCH} = \frac{SH}{HC} = \frac{a}{a\sqrt{5}} = \frac{\sqrt{5}}{5}

  • Câu 11: Vận dụng
    Côsin góc giữa đường thẳng MN và (BA’C’) bằng

    Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng . Điểm M và N lần lượt là trung điểm các đoạn AC, BB’. Côsin góc giữa đường thẳng MN và (BA’C’) bằng

    Hướng dẫn:

     Côsin góc giữa đường thẳng MN và (BA’C’) bằng

    Gọi là số đo góc giữa MN và (BA’C’), K là hình chiếu vuông góc của N lên (B’A’C’).

    Khi đó \sin \alpha = \frac{{NK}}{{NI}} = \frac{{d\left( {N;\,\,\left( {BA'C'} ight)} ight)}}{{NI}}

    Gọi E là trung điểm của A’C’, khi đó BMEB’ là hình chữ nhật. Gọi I = MN \cap BE, ta có

    MN = \sqrt {B{M^2} + B{N^2}} = 1 \Rightarrow IN = \frac{1}{3}MN = \frac{1}{3}

    Ta có \frac{{d\left( {N;\,\,\left( {BA'C'} ight)} ight)}}{{d\left( {B';\,\,\left( {BA'C'} ight)} ight)}} = \frac{{NB}}{{B'B}} = \frac{1}{2}

    \left\{ \begin{gathered} A'C' \bot B'E \hfill \\ A'C' \bot ME \hfill \\ \end{gathered} ight. \Rightarrow A'C' \bot \left( {BMEB'} ight) \Rightarrow \left( {BA'C'} ight) \bot \left( {BMEB'} ight)

    \left( {BA'C'} ight) \cap \left( {BMEB'} ight) = BE. Kẻ B'H \bot BE\,\left( {H \in BE} ight)

    \begin{matrix} \Rightarrow B'H \bot \left( {BA'C'} ight) \Rightarrow d\left( {B';\,\,\left( {BA'C'} ight)} ight) = B'H \hfill \\ B'H = \dfrac{1}{{\sqrt {\dfrac{1}{{B'{E^2}}} + \dfrac{1}{{B'{B^2}}}} }} = \dfrac{{\sqrt {21} }}{7} \hfill \\ \end{matrix}

    Từ \frac{{d\left( {N;\,\,\left( {BA'C'} ight)} ight)}}{{d\left( {B';\,\,\left( {BA'C'} ight)} ight)}} = \frac{1}{2} \Rightarrow d\left( {N;\,\,\left( {BA'C'} ight)} ight) = \frac{{\sqrt {21} }}{{14}}

    \begin{matrix} \Rightarrow \sin \alpha = \dfrac{{d\left( {N;\,\,\left( {BA'C'} ight)} ight)}}{{NI}} = \dfrac{{3\sqrt {21} }}{{14}} \hfill \\ \Rightarrow \cos \alpha = \sqrt {1 - {{\sin }^2}\alpha } = \sqrt {1 - {{\left( {\dfrac{{3\sqrt {21} }}{{14}}} ight)}^2}} = \dfrac{{\sqrt 7 }}{{14}} \hfill \\ \end{matrix}

  • Câu 12: Nhận biết
    Tính thể tích khối trụ

    Cho một khối trụ có diện tích đáy bằng 4a^{2}, chiều cao bằng a. Thể tích khối chóp đã cho là:

    Hướng dẫn:

    Ta có: \left\{ \begin{matrix} B = 4a^{2} \\ h = a \\ \end{matrix} ight.

    Thể tích khối trụ là: V = B.h = 4a^{2}.a = 4a^{3}

  • Câu 13: Nhận biết
    Chọn đáp án đúng

    Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây sai?

    Hướng dẫn:

    Hình vẽ minh họa:

    Do ABCD là hình thoi tâm O và SA = SC, SB = SD nên \left\{ \begin{matrix}SO\bot AC \\SO\bot BD \\\end{matrix} ight. => SO ⊥ (ABCD)

    Từ \left\{ \begin{matrix}SO\bot AC \\AC\bot BD \\\end{matrix} ight.=> AC ⊥ (SBD)

    Từ \left\{ \begin{matrix}SO\bot BD \\AC\bot BD \\\end{matrix} ight.=> BD ⊥ (SAC)

    Như vậy, các khẳng định “SO ⊥ (ABCD)”, “AC ⊥ (SBD)”, “BD ⊥ (SAC)” là các khẳng định đúng.

    Khẳng định “BC ⊥ (SAB)” là khẳng định sai. Vì nếu BC ⊥ (SAB) suy ra BC ⊥ SB, cùng với BC ⊥ SO ta có BC ⊥ (SBD), nên qua điểm B có hai mặt phẳng phân biệt cùng vuông góc với đường thẳng BC (vô lí).

  • Câu 14: Thông hiểu
    Xác định đường thẳng vuông góc với mặt phẳng

    Cho hình tứ diện ABCD có AB, CD, BC đôi một vuông góc. Khi đó ta có:

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có:

    \begin{matrix}\left\{ \begin{matrix}CD\bot AB \subset (ABC) \hfill \\CD\bot CB \subset (ABC) \\AB \cap CB = B \hfill \\\end{matrix} ight.\ \Rightarrow CD\bot(ABC) \hfill \\\Rightarrow CD\bot(ABC) \hfill \\\end{matrix}

    Ta có:

    Nếu AB\bot(ACD) \Rightarrow AB\botAC (Vô lí)

    Nếu BC\bot(ACD) \Rightarrow BC\botAC (Vô lí)

    Nếu AD\bot(BCD) \Rightarrow B \equivD (Vô lí)

     

  • Câu 15: Thông hiểu
    Tìm tan α

    Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của điểm S lên mặt phẳng (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Gọi α là số đo của góc giữa đường thẳng SA và mặt phẳng (ABC). Tính tan α.

    Hướng dẫn:

    Hình chiếu của SA lên mặt phẳng (ABC) là AH

    => Góc giữa SA và mặt phẳng (ABC) là \widehat{SAH}

    Tam giác ABC và SBC là các tam giác đều cùng cạnh a

    AH = SH =\frac{a\sqrt{3}}{2}

    Vậy tan α = 1

  • Câu 16: Nhận biết
    Chọn khẳng định đúng?

    Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của hai đường chéo và SA = SC. Trong các khẳng định sau, khẳng định nào đúng?

    Hướng dẫn:

    Ta có: SA = SC => SAC là tam giác cân. Mặt khác O là trung điểm của AC

    => AC ⊥ SO

    Ta có: AC ⊥ BD, AC ⊥ SO => AC ⊥ (SBD)

  • Câu 17: Nhận biết
    Trong các mệnh đề sau mệnh đề nào đúng?

    Trong các mệnh đề sau mệnh đề nào đúng?

    Hướng dẫn:

    Mệnh đề đúng là: Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song với c (hoặc b trùng với c)

  • Câu 18: Nhận biết
    Chọn đáp án đúng

    Có bao nhiêu mặt phẳng đi qua một điểm A cho trước và vuông góc với hai mặt phẳng phân biệt (P) và (Q)?

    Hướng dẫn:

    Có một khi (P) và (Q) cắt nhau, có vô số khi (P) // (Q).

  • Câu 19: Thông hiểu
    Tính góc giữa hai mặt phẳng (SCD) và (SAB)

    Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a ; AD = 2a, SA \bot \left( {ABCD} ight);SA = a\sqrt 2. Tính góc giữa hai mặt phẳng (SCD) và (SAB).

    Hướng dẫn:

     Tính góc giữa hai mặt phẳng (SCD) và (SAB)

    Gọi M là trung điểm của AD.

    Xét tứ giác ABCM có: AM // BC, AM = AB = BC = a, \widehat {MAB} = {90^0}

    Suy ra ABCM là hình vuông => MC = AB = a

    Xét tam giác ACD có AM là trung tuyến và CM = \frac{1}{2}AD = a

    Suy ra ACD vuông tại C => AC ⊥ CD

    Trong (SAC), dựng AH ⊥ SC

    Ta có: \left\{ {\begin{array}{*{20}{c}} {CD \bot AC} \\ {CD \bot SA} \\ {SA \cap AC = A} \\ {SA;AC \subset \left( {SAC} ight)} \end{array}} ight. \Rightarrow CD \bot \left( {SAC} ight) mà AH ⊂ (SAC) suy ra CD ⊥ AH.

    Ta có: \left\{ {\begin{array}{*{20}{c}} {AH \bot CD} \\ {AH \bot SC} \\ {CD \cap SC = C} \\ {CD;SC \subset \left( {SCD} ight)} \end{array}} ight. \Rightarrow AH \bot \left( {SCD} ight)\left( 1 ight)

    Ta có: \left\{ {\begin{array}{*{20}{c}} {AD \bot SA} \\ {AD \bot AB} \\ {SA \cap AB = A} \\ {SA;AB \subset \left( {SAB} ight)} \end{array}} ight. \Rightarrow AD \bot \left( {SAB} ight)\left( 2 ight)

    Từ (1) và (2) suy ra góc giữa hai mặt phẳng (SAB) và (SCD) là góc giữa hai đường thẳng AH và AD.

    Xét tam giác ABC vuông tại B có: AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2

    Xét tam giác SAC vuông tại A có: SC = \sqrt {S{A^2} + A{C^2}} = 2a

    Xét tam giác SAC vuông tại A và SA = AC = a\sqrt 2 nên SAC vuông cân tại A.

    Suy ra H là trung điểm SC và AH = \frac{1}{2}SC = a

    Xét tam giác AHD vuông tại H (vì AH ⊥ (SCD)).

    Ta có: \cos \widehat {HAD} = \frac{{AH}}{{AD}} = \frac{a}{{2a}} = \frac{1}{2} suy ra \widehat {DAH} = {60^0}

    Vậy \left( {\widehat {\left( {SCD} ight);\left( {SAB} ight)}} ight) = {60^0}

  • Câu 20: Thông hiểu
    Xác định thể tích khối chóp S.ABCD

    Khối chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA = SB = 2a. Mặt phẳng (SAB) tạo với mặt phẳng đáy một góc 90^{0}. Xác định thể tích khối chóp S.ABCD?

    Hướng dẫn:

    Hình vẽ minh họa

    Gọi H là trung điểm của AB

    Tam giác SAB cân tại S nên SH\bot AB

    Ta có: \left\{ \begin{matrix} SH\bot AB \\ (SAB)\bot(ABCD) \\ SH \subset (SAB) \\ AB = (SAB) \cap (ABCD) \\ \end{matrix} ight.\ \Rightarrow SH\bot(ABCD)

    Vậy SH là đường cao của hình chóp

    Xét tam giác AHS vuông tại H ta có:

    SH = \sqrt{SA^{2} - AH^{2}} = \sqrt{(2a)^{2} - \left( \frac{a}{2} ight)^{2}} = \frac{a\sqrt{15}}{2}

    Vậy thể tích hình chóp là:

    V = \frac{1}{3}.SH.S_{ABCD} = \frac{1}{3}.\frac{a^{2}\sqrt{15}}{2}.a^{2} = \frac{a^{3}\sqrt{15}}{6}

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (30%):
    2/3
  • Thông hiểu (55%):
    2/3
  • Vận dụng (10%):
    2/3
  • Vận dụng cao (5%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 2 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CD

Đăng nhập