Lớp 11 Toán 11 - Cánh Diều

Luyện tập Hai đường thẳng vuông góc Cánh Diều

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 14 câu
  • Điểm số bài kiểm tra: 14 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Thông hiểu
    Tứ giác MNPQ là hình gì?

    Cho tứ diện ABCD có AB vuông góc với CD. Mặt phẳng (P) song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Tứ giác MNPQ là hình gì?

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có: (MNPQ) // AB; (MNPQ) ∩ (ABC) = MQ

    => MQ // AB

    Tương tự ta có: MN // CD; NP // AB; QP // CD

    Khi đó tứ giác MNPQ là hình bình hành

    Ta có: MN ⊥ MQ (Do AB ⊥ CD)

    Hay tứ giác MNPQ là hình chữ nhật.

  • Câu 2: Thông hiểu
    Xác định cosin góc giữa hai đường thẳng SB và AC

    Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết: AB = a,AD = SA = a\sqrt 3. Hai bên mặt SAB và SAD vuông tại a. Gọi μ là góc giữa hai đường thẳng SB và AC. Tính cosμ?

    Hướng dẫn:

    Hình vẽ minh họa:

    Xác định cosin góc giữa hai đường thẳng SB và AC

    Ta có:

    \begin{matrix} \cos \left( {\overrightarrow {SB} ;\overrightarrow {AC} } ight) = \dfrac{{\overrightarrow {SB} .\overrightarrow {AC} }}{{SB.AC}} = \dfrac{{\overrightarrow {SB} .\overrightarrow {AC} }}{{4{a^2}}} \hfill \\ \overrightarrow {SB} .\overrightarrow {AC} = \left( {\overrightarrow {SA} + \overrightarrow {AB} } ight).\overrightarrow {AC} \hfill \\ = \overrightarrow {SA} .\overrightarrow {AC} + \overrightarrow {AB} .\overrightarrow {AC} \hfill \\ \end{matrix}

    Ta lại có:

    \begin{matrix} \overrightarrow {AS} .\overrightarrow {AC} = \overrightarrow {AS} .\left( {m\overrightarrow {AB} + n\overrightarrow {AC} } ight) = 0 \hfill \\ \overrightarrow {AB} .\overrightarrow {AC} = 2.2a.\cos {60^0} = {a^2} \hfill \\ \Rightarrow \cos \left( {\overrightarrow {SB} ,\overrightarrow {AC} } ight) = \frac{1}{4} \hfill \\ \Rightarrow \cos \mu = \frac{1}{4} \hfill \\ \end{matrix}

     

  • Câu 3: Thông hiểu
    Cos(AB; DM) bằng bao nhiêu?

    Cho tứ diện đều ABCD, M là trung điểm của BC. Khi đó cos(AB; DM) là:

    Hướng dẫn:

    Hình vẽ minh họa:

    Cos(AB; DM) bằng bao nhiêu?

    Giả sử cạnh của tứ diện là a

    Tam giác BCD đều => DM = \frac{{a\sqrt 3 }}{2}

    Tam giác ABC đều => AM = \frac{{a\sqrt 3 }}{2}

    Ta có: \cos \left( {\overrightarrow {AB} ;\overrightarrow {DM} } ight) = \frac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{\left| {\overrightarrow {AB} } ight|.\left| {\overrightarrow {DM} } ight|}} = \dfrac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{a.\dfrac{{a\sqrt 3 }}{2}}}

    Mặt khác 

    \begin{matrix} \overrightarrow {AB} .\overrightarrow {DM} = \overrightarrow {AB} (\overrightarrow {AM} - \overrightarrow {AD} ) \hfill \\ = \overrightarrow {AB} .\overrightarrow {AM} - \overrightarrow {AB} .\overrightarrow {AD} \hfill \\ = |\overrightarrow {AB} |.|\overrightarrow {AM} |.\cos (\overrightarrow {AB} .\overrightarrow {AM} ) \hfill \\ - |\overrightarrow {AB} |.|\overrightarrow {AD} |.\cos (\overrightarrow {AB} .\overrightarrow {AD} ) \hfill \\ = |\overrightarrow {AB} |.|\overrightarrow {AM} |.\cos {30^0} - |\overrightarrow {AB} |.|\overrightarrow {AD} |.\cos {60^0} \hfill \\ = a.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} - a.a.\dfrac{1}{2} \hfill \\ = \dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{2} = \dfrac{{{a^2}}}{4} \hfill \\ \Rightarrow \cos (\overrightarrow {AB} ,\overrightarrow {DM} ) = \dfrac{{\sqrt 3 }}{6} > 0 \hfill \\ \Rightarrow (\overrightarrow {AB} ,\overrightarrow {DM} ) = (AB,DM) \hfill \\ \Rightarrow \cos (AB,DM) = \dfrac{{\sqrt 3 }}{6} \hfill \\ \end{matrix}

  • Câu 4: Nhận biết
    Tính số đo góc giữa hai đường thẳng SA và BC

    Cho hình chóp S.ABC có AB = AC, \widehat {SAB} = \widehat {SAC}. Tính số đo góc giữa hai đường thẳng SA và BC.

    Hướng dẫn:

    Ta có:

    \begin{matrix} \overrightarrow {AS} .\overrightarrow {BC} = \overrightarrow {AS} .\left( {\overrightarrow {AC} - \overrightarrow {AB} } ight) \hfill \\ = \overrightarrow {AC} .\overrightarrow {AS} - \overrightarrow {AB} .\overrightarrow {AS} \hfill \\ = AC.AS.\cos \widehat {SAC} - AB.AS.\cos \widehat {SAB} \hfill \\ = 0 \hfill \\ \end{matrix}

    Vì AB = AC,\widehat {SAB} = \widehat {SAC}

    => Góc giữa hai đường thẳng SA, BC là: 900

  • Câu 5: Vận dụng
    Cosin của góc tạo bởi hai đường thẳng AB và DM

    Cho tứ diện ABCD có M là trung điểm của BC. Tính cosin góc giữa hai đường thẳng AB và DM.

    Hướng dẫn:

    Hình vẽ minh họa:

    Cosin của góc tạo bởi hai đường thẳng AB và DM

    Gọi N là trung điểm của AC

    I là trung điểm của MN

    Ta có:

    \left\{ {\begin{array}{*{20}{c}} {MN//AB} \\ {DI \bot MN} \end{array}} ight. \Rightarrow \left( {AB,DM} ight) = \left( {MN,DM} ight)

    => \cos \left( {AB,DM} ight) = \cos \left( {MN,DM} ight) = \cos \widehat {IMD}

    Ta có: \left\{ {\begin{array}{*{20}{c}} {DM = \dfrac{{\sqrt 3 }}{2}} \\ {MII = \dfrac{a}{4}} \end{array}} ight. \Rightarrow \cos \widehat {IMD} = \dfrac{{\sqrt 3 }}{6}

  • Câu 6: Nhận biết
    Khẳng định nào sau đây sai?

    Trong không gian cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây sai?

    Hướng dẫn:

    Mệnh đề đúng: Nếu a và b cùng vuông góc với c thì a // b

  • Câu 7: Thông hiểu
    Số đo góc giữa hai đường thẳng chéo nhau

    Cho hình chóp S.ABC có SA = SB và CA = CB. Tính số đo góc giữa hai đường thẳng chéo nhau SC và AB.

    Hướng dẫn:

    Hình vẽ minh họa:

    Số đo góc giữa hai đường thẳng chéo nhau

    \begin{matrix} \overrightarrow {SC} \overrightarrow {AB} = - \overrightarrow {CS} .(\overrightarrow {CB} - \overrightarrow {CA} ) \hfill \\ = \overrightarrow {CS} .\overrightarrow {CA} - \overrightarrow {CS} .\overrightarrow {CB} \hfill \\ = CS.CA.\cos \widehat {SCA} - CS.CB.\cos \widehat {SCB} \hfill \\ = CS.CA.\dfrac{{S{C^2} + C{A^2} - S{A^2}}}{{2SC.CA}} \hfill \\ - CS.CB.\dfrac{{S{C^2} + C{B^2} - S{B^2}}}{{2SC.CB}} \hfill \\ = \frac{{S{C^2} + C{A^2} - S{A^2}}}{2} - \dfrac{{S{C^2} + C{B^2} - S{B^2}}}{2} = 0 \hfill \\ ({\text{Do }}SA = SB{\text{ v\`a }}CA = CB) \Rightarrow SC \bot AB \hfill \\ \end{matrix}

  • Câu 8: Thông hiểu
    Góc (IE; JF) = ?

    Cho tứ diện ABCD có AB = CD. Gọi I, J E, F lần lượt là trung điểm của AC, BC, BD, AD. Góc (IE; JF) bằng:

    Hướng dẫn:

    Hình vẽ minh họa

    Ta có: IF là đường trung bình của tam giác ACD => \left\{ \begin{matrix}IF//CD \\IF = \dfrac{1}{2}CD \\\end{matrix} ight.

    JE là đường trung bình của tam giác BCD => \left\{ \begin{matrix}JE//CD \\JE = \dfrac{1}{2}CD \\\end{matrix} ight.

    => \left\{ \begin{matrix} IF = JE \\ IF//JE \\ \end{matrix} ight.=> Tứ giác IJEF là hình bình hành

    Mặt khác \left\{ \begin{matrix}IJ = \dfrac{1}{2}AB \\JE = \dfrac{1}{2}CD \\\end{matrix} ight.. MÀ AB = CD => IJ = JE

    Do đó IJEF là hình thoi => (IE; JF) = 900

  • Câu 9: Thông hiểu
    Mệnh đề nào sau đây là đúng?

    Mệnh đề nào sau đây là đúng?

    Hướng dẫn:

     

    • Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau sai vì chúng có thể chéo nhau hoặc cắt nhau.

    • Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại sai vì nó và đường thẳng còn lại có thể chéo nhau hoặc cắt nhau.

    • Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau sai vì chúng có thể song song với nhau

     

  • Câu 10: Nhận biết
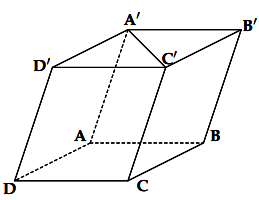
    Xác định góc giữa hai đường thẳng AC, A’D

    Cho hình hộp ABCD.A’B’C’D’. Giả sử tam giác AB’C và A’DC’ đều có ba góc nhọn. Góc giữa hai đường thẳng AC, A’D là góc nào sau đây?

    Hướng dẫn:

    Xác định góc giữa hai đường thẳng AC, A’D

    Do ACC’A’ là hình bình hành nên AC song song với A’C’. Do đó:

    \left( {\widehat {AC;A'D}} ight) = \left( {\widehat {A'C';A'D}} ight)

    Như vậy \left( {\widehat {AC;A'D}} ight) = \widehat {DA'C'}

  • Câu 11: Thông hiểu
    Số đo góc (MN; SC) bằng:

    Cho hình chóp S. ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN; SC) bằng:

    Hướng dẫn:

    Hình vẽ minh họa:

    Do ABCD là hình vuông cạnh a

    => AC = a\sqrt{2} \Rightarrow AC^{2} = 2a^{2} = SA^{2} + SC^{2}

    => Tam giác SAC vuông tại S

    Từ giả thiết ta có MN là đường trung bình của tam giác DSA

    => \overrightarrow{NM} = \frac{1}{2}\overrightarrow{SA}. Khi đó \overrightarrow{NM}.\overrightarrow{SC} = \frac{1}{2}\overrightarrow{SA}.\overrightarrow{SC} = 0

    => MN\bot SC \Rightarrow (MN;SC) = 90^{0}

  • Câu 12: Nhận biết
    Chọn khẳng định có thể sai?

    Cho hình hộp ABCD.A’B’C’D có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau. Mệnh đề nào có thể sai?

    Hướng dẫn:

    Dễ thấy các đáp án A’C’ ⊥ BD, A’B ⊥ DC’, BC’ ⊥ A’D đúng

    Đáp án BB’ ⊥ BD sẽ bị sai trong trường hợp hình hộp có cạnh bên không vuông góc với mặt đáy

  • Câu 13: Thông hiểu
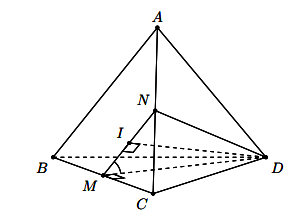
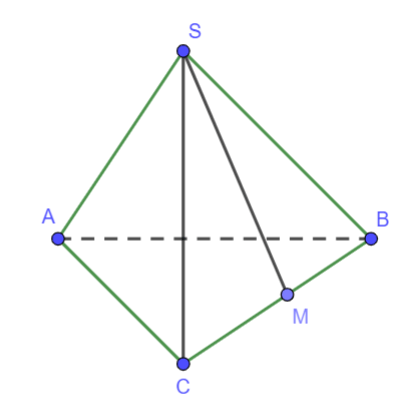
    Tính số đo góc giữa hai đường thẳng chéo chau

    Cho hình chóp S.ABC có AB = AC và \widehat {SAC} = \widehat {SAB}. Tính số đo góc giữa hai đường thẳng chéo chau SA và BC.

    Hướng dẫn:

    Hình vẽ minh họa:

    Tính số đo góc giữa hai đường thẳng chéo chau

    Xét

    \begin{matrix} \overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .(\overrightarrow {SC} - \overrightarrow {SB} ) \hfill \\ = \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB} \hfill \\ = |\overrightarrow {SA} |.|\overrightarrow {SC} |.\cos (\overrightarrow {SA} ,\overrightarrow {SC} ) - |\overrightarrow {SA} |.|\overrightarrow {SB} |.\cos \widehat {SAB} \hfill \\ = SA.SC.\cos \widehat {ASC} - SASB\cos \widehat {ASB}{\text{ }}\left( 1 ight) \hfill \\ \end{matrix}

    Ta có:

    \begin{matrix} \Rightarrow \left\{ {\begin{array}{*{20}{l}} {SA{\text{ chung }}} \\ {AB = AC} \\ {\widehat {SAB} = \widehat {SAC}} \end{array} \Rightarrow \Delta SAB = \Delta SAC(c - g - c)} ight. \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}{l}} {SC = SB} \\ {\widehat {ASC} = \widehat {ASB}} \end{array}} ight.(2) \hfill \\ \end{matrix}

    Từ (1) và (2) \Rightarrow \overrightarrow {SA} .\overrightarrow {BC} = 0 \Rightarrow SA \bot BC

  • Câu 14: Vận dụng
    Xác định góc giữa MN và AP

    Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N, P lần lượt là trung điểm của các cạng AB, BC, C’D’. Xác định góc giữa hai đường thẳng MN và AP.

    Hướng dẫn:

    Do AC song song với MN nên góc giữa hai đường thẳng MN và AP là góc giữa hai đường thẳng AC và AP.

    Ta tính được: PC = \frac{{a\sqrt 5 }}{2};AP = \frac{{3a}}{2};AC = a\sqrt 2

    \begin{matrix} \cos \left( {\widehat {CAP}} ight) = \dfrac{{A{P^2} + A{C^2} - P{C^2}}}{{2AP.AC}} = \dfrac{{\sqrt 2 }}{2} \hfill \\ \to \widehat {CAP} = {45^0} \hfill \\ \end{matrix}

0/14
14 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (29%):
    2/3
  • Thông hiểu (57%):
    2/3
  • Vận dụng (14%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 3 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CD

Đăng nhập