Lớp 11 Toán 11 - Cánh Diều

Hai đường thẳng vuông góc Cánh Diều

I. Góc giữa hai đường thẳng trong không gian

Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a' và b' cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b.

Kí hiệu (a,b) hoặc \widehat{(a,b)}.

Nhận xét:

  • Góc giữa hai đường thẳng a,b không phụ thuộc vào vị trí điểm O.
  • Góc giữa hai đường thẳng a,b bằng góc giữa hai đường thẳng b,a tức là: \widehat{(a,b)} = \widehat{(b,a)}.
  • Góc giữa hai đường thẳng không vượt quá 90^{0}.
  • Nếu a//b thì \widehat{(a,c)} = \widehat{(b,c)} với mọi đường thẳng c trong không gian.

Ví dụ: Cho tứ diện đều ABCD, M trung điểm của các cạnh BC. Xác định góc giữa hai đường thẳng AB và DM.

Hướng dẫn giải

Hình vẽ minh họa

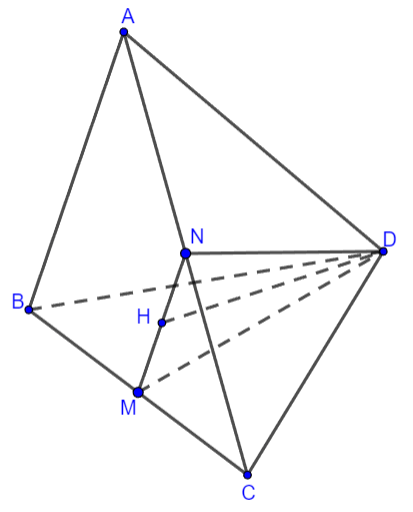
Hai đường thẳng vuông góc Cánh Diều

Gọi độ dài cạnh của tứ diện đều là 2a

Gọi N là trung điểm cạnh AC, H là trung điểm của MN, ta có:

MN//AB \Rightarrow (AB,DM) = (MN,DM)

Vì \left\{ \begin{matrix} DM = DN = a\sqrt{3} \\ MN = a \\ \end{matrix} \right. nên tam giác DMN cân tại D.

\Rightarrow MH = \frac{a}{2};DH\bot MN

\cos\widehat{DMN} = \frac{MH}{MD} = \frac{\sqrt{3}}{6} \Rightarrow \widehat{DMN} \approx 73,2^{0}

Vậy (AB,DM) = (MN,DM) = \widehat{DMN} \approx 73,2^{0}.

Câu trắc nghiệm mã số: 8849

II. Hai đường thẳng vuông góc trong không gian

Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90^{0}.

Nhận xét: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.

Ví dụ: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD,SD. Chứng minh rằng MN\bot SC.

Hướng dẫn giải

Hình vẽ minh họa

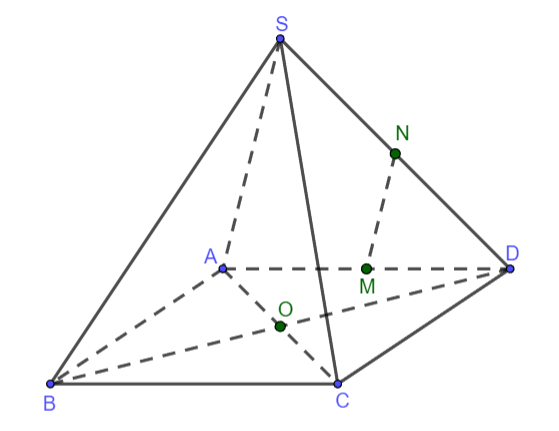
Hai đường thẳng vuông góc Cánh Diều

Xét tam giác SAD có M,N lần lượt là trung điểm các cạnh AD,SD

Suy ra MN là đường trung bình của tam giác SAD

\Rightarrow MN//SA

Vậy (MN,SC) = (SA,SC)

Ta có tam giác ABC vuông tại B nên AC = \sqrt{BC^{2} + AB^{2}} = a\sqrt{2}

Xét tam giác SAC nhận thấy AC^{2} = SA^{2} + SC^{2}

Theo định lí Pythagore đảo ta suy ra tam giác SAC vuông tại S.

\Rightarrow \widehat{ASC} = 90^{0} hay (MN,SC) = \widehat{ASC} = 90^{0}

Vậy MN\bot SC.

Câu trắc nghiệm mã số: 7655
  • 3 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CD