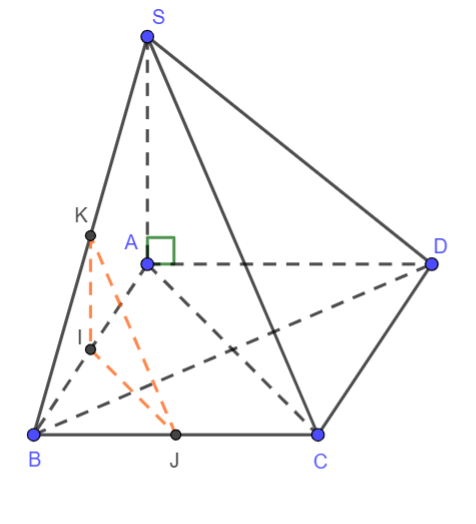
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên ![]() và SA ⊥ (ABCD). Gọi α là góc giữa đường thẳng SC và mặt phẳng (SAB). Chọn khẳng định đúng trong các khẳng định sau.
và SA ⊥ (ABCD). Gọi α là góc giữa đường thẳng SC và mặt phẳng (SAB). Chọn khẳng định đúng trong các khẳng định sau.
Ta có:
=> Hình chiếu vuông góc của BC trên mặt phẳng (SAB) là SB
=>
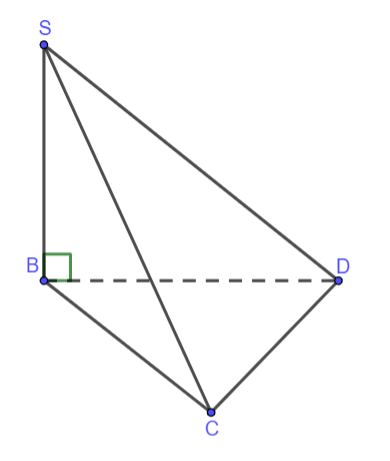
Xét tam giác SAB vuông ta có:
Xét tam giác SBC vuông ta có: