Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, góc ABC bằng 600, tam giác SBC là tam giác đều có cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Tính số đo góc giữa đường thẳng SA và mặt phẳng đáy (ABC).
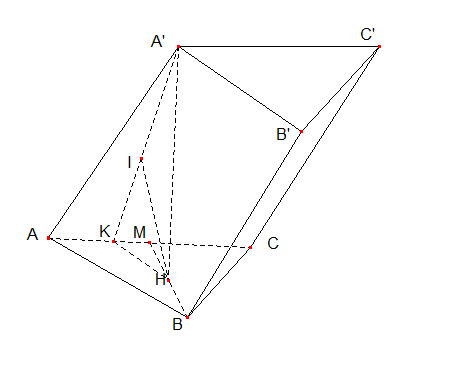
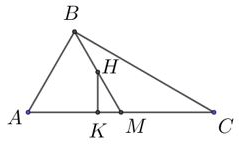
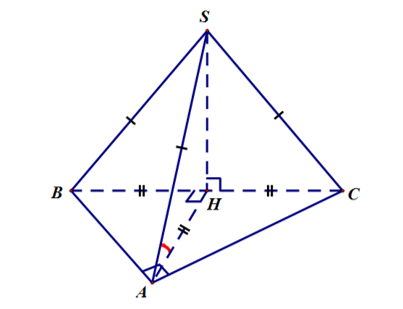
Hình vẽ minh họa:
Gọi H là trung điểm của BC => SH ⊥ (ABC)
Vì SH ⊥ (ABC) => HA là hình chiếu vuông góc của SA trên mặt phẳng (SAB)
=>
Xét tam giác SBC đều cạnh 2a =>
Tam giác ABC vuông tại A =>
Tam giác SAH vuông nên