Lớp 11 Toán 11 - Cánh Diều

Luyện tập Khoảng cách Cánh Diều

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Nhận biết
    Tỉ lệ khoảng cách

    Giả sử đường thẳng ∆ cắt mặt phẳng (P) tại M. Trên ∆ lấy hai điểm A và B. Khi đó \frac{d\left( A;(P) ight)}{d\left( B;(P) ight)} bằng:

    Hướng dẫn:

    \frac{d\left( A;(P) ight)}{d\left( B;(P) ight)} = \frac{AM}{BM}

  • Câu 2: Vận dụng
    Tính khoảng cách giữa hai đường thẳng MN và BD

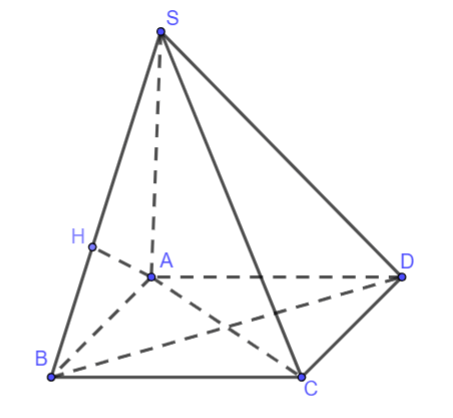
    Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của BC và DD’. Tính theo a khoảng cách giữa hai đường thẳng MN và BD.

    Hướng dẫn:

    Hình vẽ minh họa:

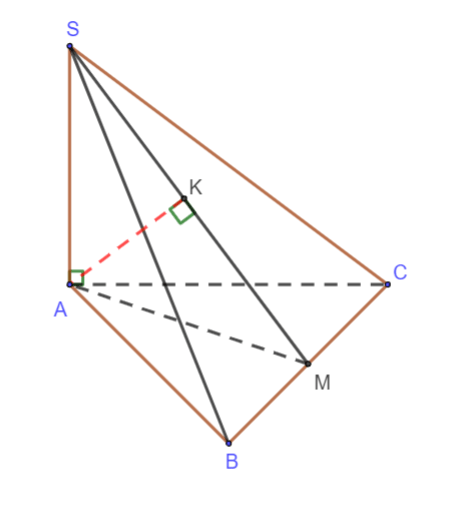
    Gọi O, P, K lần lượt là trung điểm của AC, CD, OC

    Kẻ DI ⊥ MP, DH ⊥ NI

    Ta có: ND = \frac{a}{2}, BD // MP, tứ giác DIKO là hình chữ nhật

    => DI = OK = \frac{OC}{2} =\frac{a\sqrt{2}}{4}

    Khi đó: d(MN, BD) = d(BD, (MNP)) = d(D, (MNP)) = DH

    Xét tam giác vuông NDI ta có:

    \begin{matrix}\dfrac{1}{DH^{2}} = \dfrac{1}{DN^{2}} + \dfrac{1}{DI^{2}} \Rightarrow DH =\dfrac{a\sqrt{3}}{6} \hfill \\\Rightarrow d(MN,BD) = \dfrac{a\sqrt{3}}{6} \hfill\\\end{matrix}

  • Câu 3: Nhận biết
    Chọn khẳng định đúng?

    Tìm mệnh đề đúng trong các mệnh đề sau:

    Hướng dẫn:

    Đáp án đúng: “Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.”

  • Câu 4: Thông hiểu
    Tính góc giữa AC’ và BD

    Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa AC’ và BD?

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có:

    BD ⊥ AC (do ABCD là hình vuông)

    BD ⊥ CC’

    ⇒ BD ⊥ AC’

    Do đó góc giữa AC' và BD bằng 900

  • Câu 5: Nhận biết
    Tìm khẳng định sai

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA ⊥ (ABCD). Gọi I là trung điểm của SC. Khoảng cách từ I đến mặt phẳng (ABCD) bằng độ dài đoạn thẳng nào?

    Hướng dẫn:

    Hình vẽ minh họa:

    Do I là trung điểm của SC và O là trung điểm AC nên IO ∥ SA. Do SA ⊥ (ABCD) nên IO ⊥ (ABCD), hay khoảng cách từ I đến mặt phẳng (ABCD) bằng độ dài đoạn thẳng IO

  • Câu 6: Vận dụng
    Tính khoảng cách giữa hai đường thẳng AM và B’C

    Cho hình lăng trụ đứng ABC.A’B’C’ có cạnh bên AA' = a\sqrt{2}. Biết đáy ABC là tam giác vuông có BA = BC = a, gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và B’C.

    Hướng dẫn:

    Hình vẽ minh họa:

    Gọi N là trung điểm của BB’ => MN // B’C

    => B’C // (AMN)

    => d(AM, B’C) = d(B’C, (AMN)) = d(B’, (AMN)) = d(B, (AMN))

    Kẻ BH ⊥ AM, BK ⊥ HN

    => BK ⊥ (AMN)

    => d(AM, B’C) = d(B, (AMN)) = BK

    Ta có:

    \frac{1}{BH^{2}} = \frac{1}{AB^{2}} +\frac{1}{BM^{2}}

    \Rightarrow \frac{1}{BH^{2}} =\frac{1}{a^{2}} + \frac{4}{a^{2}} = \frac{5}{a^{2}}

    \Rightarrow BH =\frac{a}{\sqrt{5}}

    Ta có: BN =\frac{a\sqrt{2}}{2}

    Do tam giác ABM vuông tại B

    \frac{1}{BK^{2}} = \frac{1}{BH^{2}} +\frac{1}{BN^{2}}

    \Rightarrow \frac{1}{BK^{2}} =\frac{5}{a^{2}} + \frac{2}{a^{2}} = \frac{7}{a^{2}}

    \Rightarrow BK =\frac{a\sqrt{7}}{7}

    \Rightarrow d(AM;B'C) =\frac{a\sqrt{7}}{7}

  • Câu 7: Thông hiểu
    Tính khoảng cách giữa hai đường thẳng IJ và SD

    Cho hình chóp SABCD có SA ⊥ (ABCD), đáy ABCD là hình thang vuông tại A và B có độ dài cạnh AB = a. Gọi I, J lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng IJ và SD.

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có AD // (IJ) ⇒ IJ // (SAD) ⇒ d(IJ, SD) = d(IJ, (SAD)) = d(I, (SAD)) = IA = a/2

  • Câu 8: Vận dụng cao
    Tính giá trị nhỏ nhất của độ dài đoạn MN

    Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Một đường thẳng d đi qua đỉnh D’ và tâm I của mặt bên BCC’B’. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC’B’) và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là:

    Hướng dẫn:

    Hình vẽ minh họa:

    Kẻ ME vuông góc với CB, tam giác MEN vuông tại E nên MN = 2EK.

    Vậy MN bé nhất khi và chỉ khi EK bé nhất.

    Lúc này EK là đoạn vuông góc chung của hai đường thẳng d và đường thẳng CB.

    Qua I kẻ P Q song song với BC (như hình vẽ).

    Vậy d(BC, d) = d(BC,(D’PQ)) = d(C, (D’PQ)) = d(C’, (D’P Q)) = C’H (trong đó C’H vuông góc với D’P).

    Ta có:

    \frac{1}{C'H^{2}} = \frac{1}{a^{2}}+ \frac{4}{a^{2}} = \frac{5}{a^{2}}

    \Rightarrow C'H =\frac{a\sqrt{5}}{2} \Rightarrow d(BC;d) =\frac{2a\sqrt{5}}{5}

  • Câu 9: Vận dụng
    Tính khoảng cách giữa hai đường thẳng AC và SB

    Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AB = 2a, AD = DC = a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa SC và mặt đáy bằng 600. Tính khoảng cách d giữa hai đường thẳng AC và SB.

    Hướng dẫn:

    Hình vẽ minh họa:

    Xác định góc 600

    \widehat{\left( SC;(ABCD) ight)} =\widehat{(SC;AC)} = 60^{0} = \widehat{SCA}

    SA = AC.tan\widehat{SCA} =a\sqrt{6}

    Gọi M là trung điểm AB => ADCM là hình vuông => CM = AD = a

    Xét tam giác ACB ta có:

    CM = a = \frac{1}{2}AB

    => Tam giác ACB vuông tại C

    Lấy điểm E sao cho ACBE là hình chữ nhật

    => AC // BE

    => d(AC, SB) = d(AC, (SBE)) = d(A,(SBE))

    Kẻ AK ⊥ SE. Khi đó:

    d\left( A;(SBE) ight) = AK =\frac{SA.AE}{\sqrt{SA^{2} + AE^{2}}} = \frac{a\sqrt{6}}{2}

  • Câu 10: Nhận biết
    Mệnh đề nào là mệnh đề sai?

    Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và A’C’ bằng:

    Hướng dẫn:

    Do BD và A’C’ lần lượt nằm trên hai mặt phẳng (ABCD) và (A’B’C’D’) song song với nhau nên d(A’C’, BD) = d((ABCD),(A’B’C’D’)).

    Mà ABCD.A’B’C’D’ là hình lập phương nên ta có d((ABCD), (A’B’C’D’)) = AA’ = a. Vậy d(A’C’, BD) = a.

  • Câu 11: Vận dụng
    Tính khoảng cách d giữa hai đường thẳng SA và BD

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách d giữa hai đường thẳng SA và BD.

    Hướng dẫn:

    Hình vẽ minh họa:

    Gọi I là trung điểm của AD

    => SI ⊥ AD => SI ⊥ (ABCD)

    Kẻ Ax // BD

    Ta có d(BD, SA) = d (BD, (SAx)) = d (D, (SAx)) = 2d (I, (SAx))

    Kẻ IE ⊥ Ax, kẻ IK ⊥ SE

    Khi đó d (I, (SAx)) = IK

    Gọi F là hình chiếu của I trên BD, ta có: IE = IF = \frac{AO}{2} =\frac{a\sqrt{2}}{4}

    Xét tam giác vuông SIE ta có:

    IK = \frac{SI.IE}{\sqrt{SI^{2} +IE^{2}}} = \frac{a\sqrt{21}}{14}

    => d(BD;SA) = 2IK =\frac{a\sqrt{21}}{7}

  • Câu 12: Thông hiểu
    Tính khoảng cách d từ A đến mặt phẳng (SBC)

    Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA=a\sqrt{3} và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC). 

    Hướng dẫn:

    Hình vẽ minh họa:

    Tính khoảng cách d từ A đến mặt phẳng (SBC)

    Gọi M là trung điểm BC 

    =>AM ⊥ BC và AM = \frac{{a\sqrt 3 }}{2}

    Gọi K là hình chiếu của A trên SM => AK ⊥ SM (1)

    Ta có: \left\{ \begin{gathered} AM \bot BC \hfill \\ BC \bot SA \hfill \\ \end{gathered} ight.

    \Rightarrow BC \bot (SAM) \Rightarrow BC \bot AK{\text{ }}\left( 2 ight)

    Từ (1) và (2) => AK⊥(SBC) => d(A;(SBC)) = AK

    Xét tam giác SAM ta có:

    AK = \frac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }} = \frac{{a\sqrt {15} }}{5}

    Vậy d(A;(SBC)) = AK = \frac{{a\sqrt {15} }}{5}

  • Câu 13: Thông hiểu
    Tính khoảng cách d từ O đến mặt phẳng (SBC)

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên SA=\frac{a\sqrt{15}}{2} và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ O đến mặt phẳng (SBC)

    Hướng dẫn:

    Ta có: 

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {AO \cap \left( {SBC} ight) = C} \\ {AC = 2OC} \end{array}} ight. \hfill \\ \Rightarrow d\left( {A;\left( {SBC} ight)} ight) = 2d\left( {O;\left( {SBC} ight)} ight) \hfill \\ \left\{ {\begin{array}{*{20}{c}} {SA \bot \left( {ABCD} ight) \Rightarrow SA \bot BC} \\ {AB \bot BC} \end{array}} ight. \hfill \\ \Rightarrow BC \bot \left( {SAB} ight) \hfill \\ \end{matrix}

    Từ A kẻ AH \bot SB => AH \bot \left( {SBC} ight)

    \begin{matrix} \Rightarrow AH = d\left( {A;\left( {SBC} ight)} ight) \hfill \\ \dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}} \hfill \\ \Rightarrow AH = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{a\sqrt {285} }}{{19}} \hfill \\ \Rightarrow d\left( {O;\left( {SBC} ight)} ight) = \dfrac{1}{2}AH = \dfrac{{a\sqrt {285} }}{{19}} \hfill \\ \end{matrix}

  • Câu 14: Thông hiểu
    Tính khoảng cách giữa hai đường thẳng

    Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a; SA = a;SA\bot(ABCD). Khoảng cách giữa hai đường thẳng SC;BD bằng bao nhiêu?

    Hướng dẫn:

    Hình vẽ minh họa

    Dựng Cx//BD;(\alpha) = (SC;Cx)

    \Rightarrow d(BD;SC) = d\left( BD;(\alpha) ight)

    d\left( BD;(\alpha) ight) = d\left( O;(\alpha) ight) = \frac{1}{2}d\left( A;(\alpha) ight)

    Dựng AK\bot SC. Dễ thấy AK\bot(\alpha) \Rightarrow d\left( A;(\alpha) ight) = AK

    \frac{1}{AK^{2}} = \frac{1}{SA^{2}} + \frac{1}{AC^{2}} \Rightarrow AK = \frac{a\sqrt{6}}{3}

    \Rightarrow d\left( O;(\alpha) ight) = \frac{a\sqrt{6}}{3}

  • Câu 15: Thông hiểu
    Tính khoảng cách d từ D đến mặt phẳng (SBC)

    Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB=a\sqrt{2}.Cạnh bên SA = 2a và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ D đến mặt phẳng (SBC)

    Hướng dẫn:

    Hình vẽ minh họa

    Tính khoảng cách d từ D đến mặt phẳng (SBC)

    Ta có: AD // BC => d\left( {D;\left( {SCD} ight)} ight) = d\left( {A;\left( {SBC} ight)} ight)

    Gọi H là hình chiếu vuông góc của A lên SB => AK \bot SB (*)

    Ta có: \left\{ {\begin{array}{*{20}{c}} {BC \bot SA} \\ {BC \bot AB} \end{array}} ight. \Rightarrow BC \bot \left( {SAB} ight) \Rightarrow BC \bot AH\left( {**} ight)

    Từ (*) và (**) => AH \bot \left( {SBC} ight)

    \begin{matrix} d\left( {A;\left( {SBC} ight)} ight) = AH \hfill \\ \Rightarrow AH = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{2a\sqrt 3 }}{3} \hfill \\ \end{matrix}

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (27%):
    2/3
  • Thông hiểu (40%):
    2/3
  • Vận dụng (27%):
    2/3
  • Vận dụng cao (7%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 2 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CD

Đăng nhập