Trong các phát biếu dưới đây phát biểu nào đúng:
Phát biểu đúng là: "Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính OA và A thuộc đường tròn."
Từ một điểm A ở bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Tứ giác AMON là hình gì?
Hình vẽ minh họa
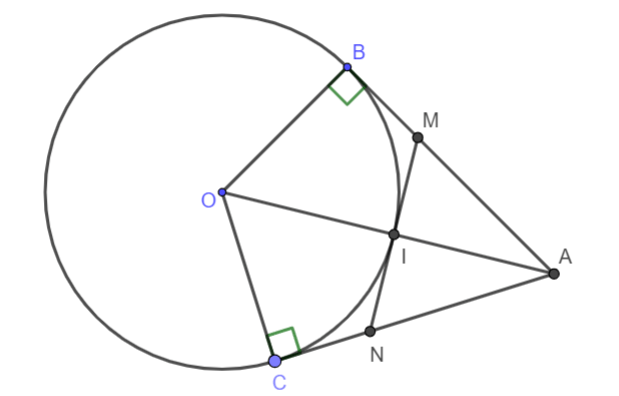
Xét tứ giác AMNO ta có:
Vì AM; ON cùng vuông góc với OB => AM // ON
Tương tự AN, OM cùng vuông góc với OC => AN // ON
=> AMON là hình bình hành
Xét hai tam giác vuông OBM và OCN ta có:
OB = OC = R
(cùng phụ với góc
)
=>
=> Tứ giác AMON là hình thoi.
“Nếu một đường thẳng đi qua một điểm của đường tròn và… thì đường thẳng ấy là một tiếp tuyến của đường tròn”. Cụm từ thích hợp điền vào chỗ trống là:
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Cho đường tròn (O), A, B, C là 3 điểm thuộc đường tròn sao cho tam giác ABC cân tại A. Phát biểu nào sau đây đúng? Tiếp tuyến của đường tròn tại A là:
Ta có:
Tam giác ABC cân tại A
=> Tâm đường tròn ngoại tiếp nằm trên đường cao của tam giác đi qua A hay OA vuông góc với BC mà tiếp tuyến của (O) tại A thì cũng phải vuông góc với OA (tính chất tiếp tuyến của đường tròn).
=> Tiếp tuyến tại A với đường tròn (O) là đường thẳng qua A và song song với BC.
Cho tam giác ABC có AC = 3cm, AB = 4cm; BC = 5cm. Vẽ đường tròn (M; NM). Khẳng định nào sau đây là đúng?
Xét tam giác ABC ta có:
=> Tam giác ABC vuông tại A
=>
Mà điểm A thuộc (C; CA)
=> AB là tiếp tuyến của (C; CA).
Cho tam giác ABC cân tại A; đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AI?
Hình vẽ minh họa
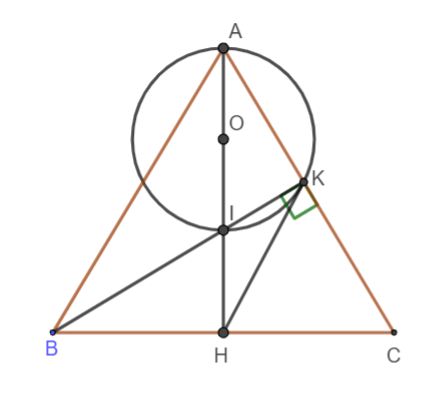
Gọi O là trung điểm AI. Xét tam giác vuông AIK có
Xét tam giác OKA cân tại O (vì OA = OK =R) có:
Xét tam giác CKB vuông tại K (vì KB⊥AC) có:
H là trung điểm CB (vì tam giác ABC cân tại A có AH là đường cao nên đồng thời là đường trung tuyến)
=> KH là trung tuyến ứng với cạnh huyền BC
Từ (1) và (2) suy ra
(Vì AH⊥BC)
Mà
Từ (*) và (**) => HK là tiếp tuyến của (O).
Cho (O; 5cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 5cm), khi đó:
Khoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bán kính của đường tròn đó.
Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau:
Hình vẽ minh họa
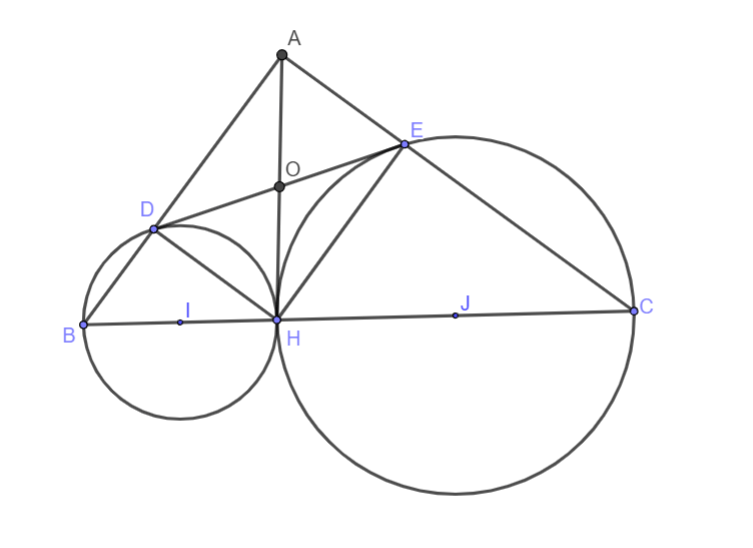
Gọi I, J lần lượt là trung điểm của BH và CH.
Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh ID ⊥ DE hay
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC
=>
=> Tứ giác ADHE là hình chữ nhật
Gọi O là giao điểm của AH và DE
=> OD = OH = OE = OA
=> Tam giác ODH cân tại O
=>
Ta cũng có tam giác IDH cân tại I
=> Phương án sai là: "DE là cát tuyến của đường tròn đường kính BH".
Cho hình chữ nhật ABCD, H là hình chiếu của A trên BD. M, N lần lượt là trung điểm của BH, CD. Đường nào sau đây là tiếp tuyến của đường tròn tâm A, bán kính AM?
Hình vẽ minh họa
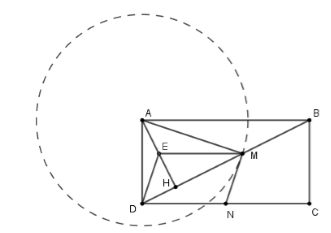
Lấy E là trung điểm của AH. Do M là trung điểm của BH (gt) nên EM là đường trung bình của tam giác AHB
=> (1)
Hình chữ nhật ABCD có CD // AB và CD = AB mà N là trung điểm của DC
=> (2)
Từ (1) và (2) => EM // DN và EM = DN
=> Tứ giác EMND là hình bình hành => DN // EM.
Mà DN ⊥ AD => EM ⊥ AD (tính chất hình chữ nhật)
AH ⊥ DM (gt)
=> E là trực tâm của ∆ADM
=> DE ⊥ AM mà DE // MN (chứng minh trên)
=> MN ⊥ AM tại M.
Vì vậy MN là tiếp tuyến của đường tròn (A; AM).
Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H. Gọi M là trung điểm BC. Đường tròn (F) ở trên nhận các đường thẳng nào dưới đây là tiếp tuyến?
Hình vẽ minh họa
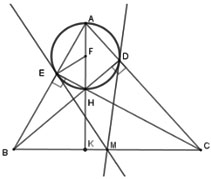
AH cắt BC tại K AK BC vì H là trực tâm tam giác ABC
Ta chứng minh ME EF tại E
FAE cân tại F (vì FA = FE) nên
MEC cân tại M (vì ) nên
Mà (cùng phụ với
) nên
Từ đó ME là tiếp tuyến của
Tương tự ta cũng có MD là tiếp tuyến của .
Vậy ME; MD là tiếp tuyến cần tìm.
