Chọn khẳng định đúng. Cho đường tròn (O) có dây AB > CD khi đó:
Cho đường tròn (O) có dây AB > CD khi đó cung AB lớn hơn cung CD.
Chọn khẳng định đúng. Cho đường tròn (O) có cung MN < cung PQ, khi đó:
Cho đường tròn (O) có cung MN < cung PQ, khi đó MN < PQ.
Cho đường tròn (O) có hai dây AB, CD song song với nhau. Kết luận nào sau đây là đúng?
Hình vẽ minh họa
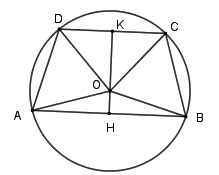
Kẻ KH ⊥ CD và KH ⊥ AB lần lượt tại K và H
=> OK vừa là đường cao, vừa là đường phân giác của
Và OH vừa là đường cao, vừa là đường phân giác của
=> Số đo cung AD bằng số đo cung BC => AD = BC
Chọn khẳng định đúng.
Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy
Trong một đường tròn, đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại
Chọn khẳng định sai.
Trong một đường tròn, đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Trong một đường tròn, cung lớn hơn căng dây lớn hơn
Hai đường kính của đường tròn luôn bằng nhau nhưng chưa chắc đã vuông góc với nhau.
Cho tam giác ABC cân tại A và 
nội tiếp đường tròn (O). Trong các cung nhỏ AB; BC; AC, cung nào là cung lớn nhất?
Hình vẽ minh họa
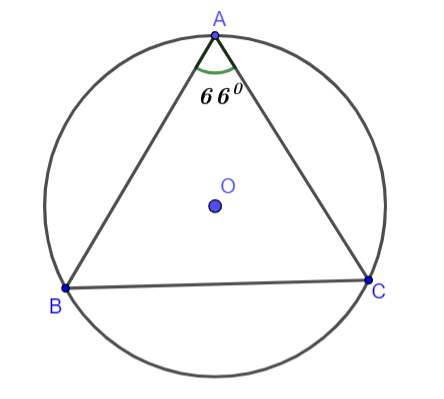
Ta có ABC là tam giác cân tại A
Vì nên theo mối liên hệ giữa cạnh và góc trong tam giác suy ra BC > AB = AC
=> Cung lớn nhất là cung BC.
Cho tam giác ABC có , đường trung tuyến AM, đường cao CH. Vẽ đường tròn ngoại tiếp BHM. Kết luận nào sai khi nói về các cung HB; MB; MH của đường tròn ngoại tiếp tam giác MHB?
Hình vẽ minh họa
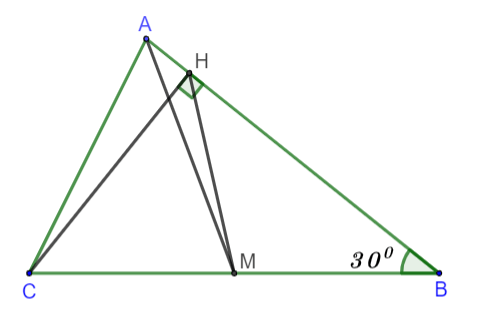
Vì trong một đường tròn hai cung bằng nhau căng hai dây bằng nhau nên ta đi so sánh các đoạn thẳng HB; MB; MH
Xét tam giác BCH vuông tại H có:
Xét tam giác HBC vuông tại H có HM là trung tuyến ứng với cạnh huyền
=>
Mặt khác
Từ (*) và (**) ta được:
=> Cung MB = Cung HM < Cung HB
Hay cung HB là cung lớn nhất.
Cho đường tròn (O; R) có hai dây cung AB và CD vuông góc với nhau tại I (C thuộc cung nhỏ AB). Kẻ đường kính BE của (O). Đẳng thức nào sau đây là đúng?
Hình vẽ minh họa
Xét đường tròn (O) có BE là đường kính và
mà
=> Cung AC bằng cung ED hay
Xét các tam giác vuông và
ta có:
Mà BED vuông tại D
Vậy
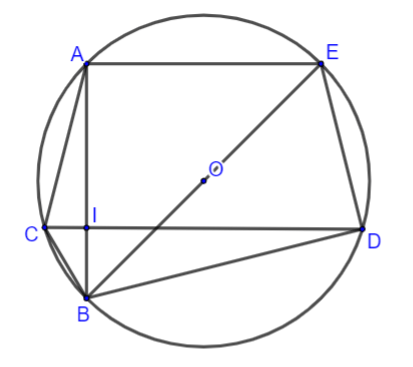
Cho đường tròn (O) đường kính AB và đường tròn (O’) đường kính AO. Các điểm C, D thuộc đường tròn (O) sao cho B thuộc cung CD và cung BC nhơ bằng cung BD nhỏ. Các dây cung AC và AD cắt đường tròn (O’) theo thứ tự E và F. So sánh cung OE và cung OF của đường tròn (O’)
Hình vẽ minh họa
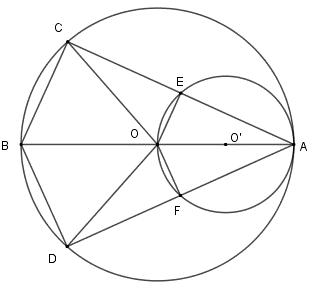
Xét (O’) với OA là đường kính và
Tương tự với (O) ta có BC AC nên OE // BC mà O là trung điểm của AB
=> E là trung điểm của AC
Tương tự mà cung BC bằng cung BD nên
hay cung OE = cung OF.
Cho đường tròn (O; R) có hai dây cung AB và CD vuông góc với nhau tại I (C thuộc cung nhỏ AB). Kẻ đường kính BE của (O). Đẳng thức nào sau đây là sai?
Hình vẽ minh họa
Xét (O) có BE là đường kính và A ∈ (O) ⇒ AE ⊥ AB mà CD ⊥ AB
⇒ AE // CD
Nên cung AC bằng cung ED hay AC = ED
Xét các tam giác vuông ∆IAC và ∆IBD ta có:
IA2 + IC2 = AC2; IB2 + ID2 = BD2
⇒ IA2 + IC2 + IB2 + ID2 = AC2 + BD2 = ED2 + BD2
Mà BED vuông tại D nên ED2 + BD2 = EB2
Hay IA2 + IC2 + IB2 + ID2 = BE2 nên C đúng mà BE ≠ AD nên "IA2 + IC2 + IB2 + ID2 = AD2" sai.
Xét các tam giác vuông ∆IAD và ∆IBC ta có:
IA2 + ID2 = AD2; IB2 + IC2 = BC2
=> IA2 + IC2 + IB2 + ID2 = AD2 + BC2
