Tâm đường tròn nội tiếp tam giác là?
Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác các góc trong tam giác.
Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai?
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Cho tam giác ABC cân tại A, I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp trong góc A. Gọi O là trung điểm của IK. Tâm của đường tròn đi qua bốn điểm B, I, C, K là:
Hình vẽ minh họa
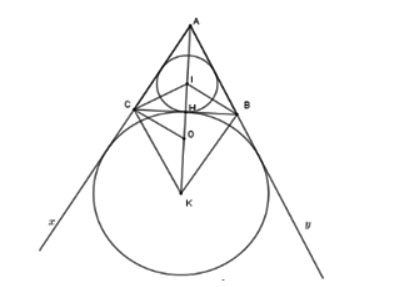
Gọi H là giao của BC và AI.
Vì tam giác ABC nên I, K thuộc AH.
Ta có:
Tương tự ta cũng có:
Xét hai tam giác vuông ICK và IBK ta có:
=> Bốn điểm B, I, C, K nằm trên đường tròn
Vậy tâm của đường tròn đi qua bốn điểm B, I, C, K là điểm O.
Số đường tròn nội tiếp của tam giác là?
Tâm của đường tròn nội tiếp tam giác là giao của ba đường phân giác góc trong tam giác.
=> Mỗi tam giác chỉ có 1 đường tròn nội tiếp.
Tâm đường tròn bàng tiếp tam giác là:
Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác.
=> Tâm đường tròn bàng tiếp tam giác là giao của 1 đường phân giác góc trong và hai đường phân giác góc ngoài của tam giác.
“Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi… Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi…”. Hai cụm từ thích hợp vào chỗ trống lần lượt là:
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Cho hình vẽ, MA và MB là hai tiếp tuyến của đường tròn (O; 3cm), MA = 4cm.
Độ dài đoạn thẳng AB là:
Vì MA và MB là tiếp tuyến nên MA = MB
=> M thuộc trung trực của AB
Mà OA = OB do cùng là bán kính nên O thuộc trung trực của AB
=> OM là trung trực của AB. Gọi H là giao điểm của MO và AB, ta có AH = BH
Xét tam giác vuông AMO vuông tại A (do MA là tiếp tuyến) có AH là đường cao.
Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Biết OB = 3cm; OA = 5cm. Vẽ đường kính CD của (O). Tính BD.
Hình vẽ minh họa
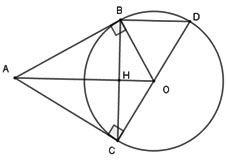
Gọi H là giao của BC với AO.
Xét (O) có hai tiếp tuyến tại B và C cắt nhau tại A => AB = AC (tính chất)
Lại có OB = OC nên AO là đường trung trực của đoạn BC hay AO ⊥ BC tại H là trung điểm của BC
Xét tam giác BCD có H là trung điểm BC và O là trung điểm DC
=> HO là đường trung bình của tam giác BCD
Xét tam giác ABO vuông tại B có BH là đường cao.
Theo hệ thức lượng trong tam giác vuông ta có:
Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I. Đường thẳng qua I và vuông góc với IA cắt OB tại K. Chọn khẳng định đúng.
Hình vẽ minh họa
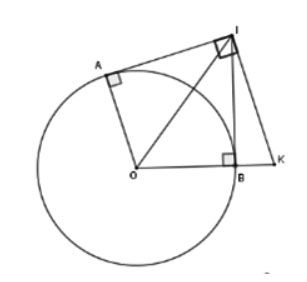
Xét đường tròn (O) có IA , IB là hai tiếp tuyến cắt nhau tại I nên
Mà OA // KI (vì cùng vuông góc với AI) nên (hai góc ở vị trí so le trong)
Từ đó: => Tam giác KOI cân tại K.
=>
Cho đường tròn (O), bán kính OA. Dây CD là đường trung trực của OA. Tứ giác OCAD là hình gì?
Hình vẽ minh họa
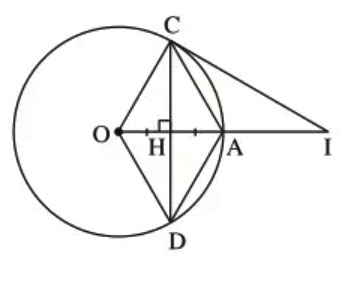
Gọi H là giao điểm của OA và CD
Vì CD là đường trung trực của OA nên tại H và
Mà OH là một phần của đường kính, CD là dây cung nên H là trung điểm của CD.
Vì tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm mỗi đường là H và cũng vuông góc với nhau tại H => Tứ giác ACOD là hình thoi.
