Lớp 9 Toán 9

Luyện tập Một số hệ thức về cạnh và góc trong tam giác vuông

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 10 câu
  • Điểm số bài kiểm tra: 10 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Nhận biết
    Chọn câu nào đúng

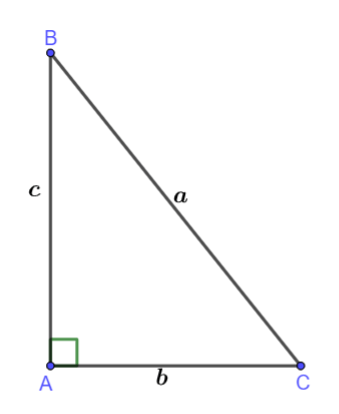
    Cho tam giác ABC có đường cao AH. Hệ thức sau là điều kiện đủ để tam giác ABC vuông tại A. Câu nào sau đây đúng?

    Hướng dẫn:

    Định lí Py - ta - go đảo

    Nếu tam giác ABC có bình phương độ dài cạnh BC bằng tổng bình phương độ dài hai cạnh AB và AC thì suy ra góc BAC bằng 900 (hay tam giác ABC vuông tại A)

    AB2 + AC2 = BC2

     

  • Câu 2: Vận dụng
    Chọn đáp án đúng

    Câu nào sau đây đúng?

    Trong tất cả các tam giác vuông có cạnh huyền bằng a thì tổng bình phương đường trung tuyến của chúng đều bằng:

    Hướng dẫn:

    Hình vẽ minh họa

    Chọn đáp án đúng

    Theo đề ta ta có 

    Ta có trong tam giác vuông đường trung tuyến cắt cạnh huyền bằng \dfrac{1}{2} cạnh huyền từ đó suy ra BM^2=\frac{1}{2} AC^2 (1)

    Ta có: AH^2 = AB^2 +BH^2 (vì tam giác ABH vuông tại B)

    = AB^2+ (\dfrac{1}{2}BC)^2=AB^2+\dfrac{1}{4}BC^2 (do AH là trung tuyến BC) (2)

    Tương tự ta có CN^2= BC^2 +BN^2=BC^2+\dfrac{1}{4}AB^2 (3)

    Lấy (2)+(3) ta có

    AB^2+\frac{1}{4} BC^2+BC^2+\frac{1}{4}AB^2

    =\frac{5}{4} AB^2+\frac{5}{4} BC^2 = \frac{5}{4} AC^2(4)

    Lấy (1)+(4) suy ra: BM^2+AH^2+CN^2 = \dfrac{3}{2} AC^2 =1,5a^2

  • Câu 3: Nhận biết
    Tính độ dài AH

    Cho tam giá ABC vuông tại C. Biết góc A = 600, AC = 8. Vẽ CH vuông góc với AB. Độ dài AH là:

    Hướng dẫn:

    Hình vẽ minh họa

    Tính độ dài AH

    Xét tam giác ACH vuông tại H ta có:

    \begin{matrix} \cos \widehat A = \dfrac{{AH}}{{AC}} \hfill \\ \Rightarrow AH = AC.\cos \widehat A = 8.\cos {60^0} = 4 \hfill \\ \end{matrix}

  • Câu 4: Thông hiểu
    Tính độ dài AC

    Cho tam giác ABC vuông tại C, CD là đường cao ứng với cạnh BC, AD=9, BD=16. Độ dài cạnh AC là:

    Hướng dẫn:

    Hình vẽ minh họa

    Tính độ dài AC

    Ta có:

    AB = AD+DB=9+16=25

    Áp dụng hệ thức lượng trong tam giác vuông ta có:

    \begin{matrix} A{C^2} = AD.AB \hfill \\ \Rightarrow AC = \sqrt {AD.AB} \hfill \\ \Rightarrow AC = \sqrt {9.25} = 15 \hfill \\ \end{matrix}

  • Câu 5: Vận dụng
    Tính tỉ số HB/HC

    Cho tam giác ABC vuông tại A có AB=2AC, AH là đường cao.Tỉ số \frac{{HB}}{{HC}} là:

    Hướng dẫn:

    Hình vẽ minh họa

    Tính tỉ số HB/HC

    Áp dụng hệ thức lượng trong tam giác vuông ta có:

    \begin{matrix} \left\{ \begin{gathered} A{C^2} = CH.BC \hfill \\ A{B^2} = HB.BC \hfill \\ \end{gathered} ight. \Rightarrow \left\{ \begin{gathered} CH = \dfrac{{A{C^2}}}{{BC}} \hfill \\ BH = \dfrac{{A{B^2}}}{{BC}} \hfill \\ \end{gathered} ight. \hfill \\ \Rightarrow \dfrac{{BH}}{{CH}} = \dfrac{{\dfrac{{A{B^2}}}{{BC}}}}{{\dfrac{{A{C^2}}}{{BC}}}} = \dfrac{{A{B^2}}}{{BC}}.\dfrac{{BC}}{{A{C^2}}} = \dfrac{{4A{C^2}}}{{A{C^2}}} = 4 \hfill \\ \end{matrix}

  • Câu 6: Thông hiểu
    Tính chiều cao cột điện

    Các tia nắng mặt trời tạo với mặt đất góc 350. Bóng của một cột điện dài 10,7m. Chiều cao của cột điện đúng nhất là:

    Hướng dẫn:

     Hình vẽ minh họa

    Tính chiều cao cột điện

    Gọi chiều dài cột điện là x (m) (x > 0)

    Áp dụng hệ thức lượng trong tam giác vuông ta có:

    \begin{matrix} \tan {35^0} = \dfrac{x}{{10,7}} \hfill \\ \Rightarrow x = 10,7.\tan {35^0} \approx 7,5 \hfill \\ \end{matrix}

    Chiều dài cột điện khoảng 7,5m.

  • Câu 7: Nhận biết
    Chọn hệ thức đúng

    Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?

    Hướng dẫn:

    Hình vẽ minh họa

    Chọn hệ thức đúng

    \sin \widehat P = \frac{{MN}}{{MP}} \Rightarrow MN = MP.\sin \widehat P

  • Câu 8: Nhận biết
    Chọn hệ thức đúng

    Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?

    Hướng dẫn:

    Hình ảnh minh họa

    Chọn hệ thức đúng

    \cot \widehat P = \frac{{NP}}{{MN}} \Rightarrow NP = MN.\cot \widehat P

  • Câu 9: Thông hiểu
    Chọn khẳng định sai

    Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai?

    Hướng dẫn:

    Hình vẽ minh họa

    Chọn khẳng định sai

    Ta có:

    \begin{matrix} \tan \widehat B = \dfrac{{AC}}{{AB}} = \dfrac{b}{c} \hfill \\ \Rightarrow b = c.\tan \widehat B \hfill \\ \cot \widehat C = \dfrac{{AC}}{{AB}} = \dfrac{b}{c} \hfill \\ \Rightarrow b = c.\cot \widehat C \hfill \\ \end{matrix}

  • Câu 10: Thông hiểu
    Tính BC

    Cho tam giác ABC có AB = 16, AC = 14 và \hat{B} =60^0. Tính BC.

    Hướng dẫn:

    Hình vẽ minh họa

    Tính BC

    Áp dụng hệ thức lượng trong tam giác ta có:

    \begin{matrix} \sin \widehat B = \dfrac{{AH}}{{AB}} \hfill \\ \Rightarrow AH = 16.\sin {60^0} = 8\sqrt 3 \hfill \\ \cos \widehat B = \dfrac{{BH}}{{AB}} \hfill \\ \Rightarrow BH = 16.\cos {60^0} = 8 \hfill \\ \end{matrix}

    Áp dụng định lí Py - ta - go ta có:

    \begin{matrix} A{H^2} + H{C^2} = A{C^2} \hfill \\ \Rightarrow HC = \sqrt {A{C^2} - A{H^2}} \hfill \\ \Rightarrow HC = \sqrt {{{14}^2} - {{\left( {8\sqrt 3 } ight)}^2}} = 2 \hfill \\ \end{matrix}

    => BC = HC + HB = 2 + 8 = 10.

0/10
10 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (40%):
    2/3
  • Thông hiểu (40%):
    2/3
  • Vận dụng (20%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 13 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 9

Đăng nhập