Lớp 9 Toán 9

Luyện tập Ôn tập chương 3 Góc với đường tròn

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 10 câu
  • Điểm số bài kiểm tra: 10 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Thông hiểu
    Tính chất tứ giác ABEC

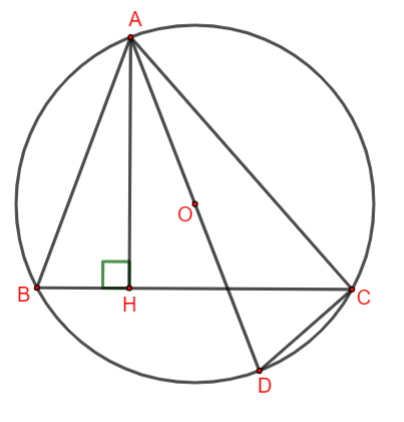
    Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Khi đó tứ giác ABEC là:

    Hướng dẫn:

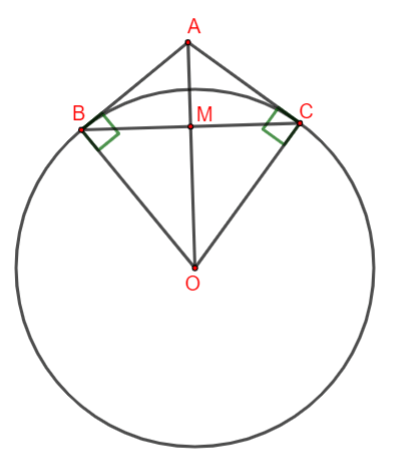
    Hình ảnh minh họa

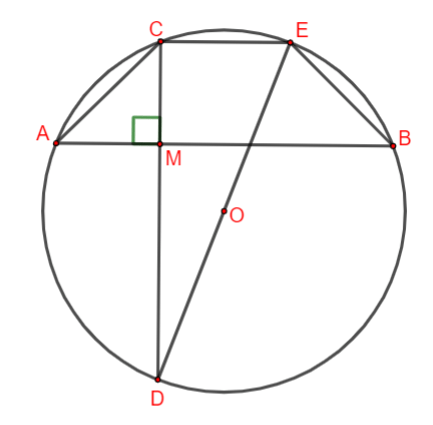
    Tính chất tứ giác ABEC

    Ta có: DE là đường kính => \widehat {DCE} = {90^0}

    => CD ⊥ CE

    CD ⊥ AB (gt)

    => AB // CE

    => Tứ giác ABEC là hình thang (1).

    Mặt khác: CE và AB là hai dây song song của đường tròn (O) chắn hai cung AC và BE.

    Từ (1) và (2) => Tứ giác ABEC là hình thang cân.

  • Câu 2: Vận dụng
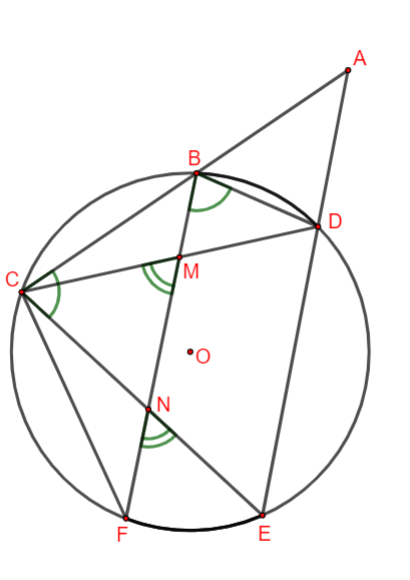
    Chọn kết luận đúng

    Qua điểm A nằm ngoài đường tròn (O) kẻ hai cát tuyến ABC và ADE với đường tròn đó (B nằm giữa A và C, D nằm giữa A và E). Kẻ dây BF // DE. Khi đó kết luận đúng là:

    Hướng dẫn:

    Hình vẽ minh họa

    Chọn kết luận đúng

    Gọi BmD là cung nhỏ BD, FnE là cung nhỏ FE.

    Ta có: \widehat {BCD} là góc nội tiếp chắn cung BmD. (1)

    \widehat {FCE} là góc nội tiếp chắn cung FnE (2)

    Mặt khác ta có:

    sdBmD = sdFnE (3) (hai cung bị chắn bởi hai dây song song)

    Từ (1); (2); (3)

    \begin{matrix} =>\widehat {FCE} = \widehat {BCD} \hfill \\ \Rightarrow \widehat {FCE} + \widehat {ECD} = \widehat {FCE} + \widehat {ECD} \hfill \\ \Rightarrow \widehat {FCD} = \widehat {ECB}\left( 4 ight) \hfill \\ \end{matrix}

    Theo tính chất về góc có đỉnh bên ngoài đường tròn ta có:

    \widehat {CAE} = \frac{1}{2}\left( {sdCFE - sdBmD} ight)

    \Rightarrow \widehat {CAE} = \frac{1}{2}\left( {sdCFE - sdFnE} ight) = \frac{1}{2}sdCF (5)

    Theo tính chất của góc nội tiếp bị chắn bởi cung ta có:

    \widehat {CDF} = \frac{1}{2}sdCF (6)

    Từ (5) và (6) ta nhận được: \widehat {CAE} = \widehat {CDF} (7)

    Từ (4) và (7) ta nhận được: \Delta ACE \sim \Delta DCF\left( {g - g} ight)

    \begin{matrix} \Rightarrow \dfrac{{AC}}{{DC}} = \dfrac{{AE}}{{DF}} = \dfrac{{CE}}{{CF}} \hfill \\ \Rightarrow AC.DF = AE.DC \hfill \\ \end{matrix}

  • Câu 3: Vận dụng
    Chọn câu đúng

    \begin{matrix} \Rightarrow \Delta MEA \sim \Delta DEM \hfill \\ \Rightarrow \dfrac{{ME}}{{DE}} = \dfrac{{EA}}{{EM}} \Rightarrow E{M^2} = DE.EA\left( 2 ight) \hfill \\ \end{matrix}Từ điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB với (O) tại A và B. Qua A vẽ đường thẳng song song với MB cắt đường tròn tại C

     Chọn câu đúng

    Nối C với M cắt đường tròn (O) tại D. Nối A với D cắt MB tại E. Chọn câu đúng

    Hướng dẫn:

    Xét tam giác ABE và BDE ta có:

    Góc E là góc chung

    \widehat {BAE} = \widehat {DBE} (góc nội tiếp và góc giữa tia tiếp tuyến và dây cung cùng chắn cung BD)

    \begin{matrix} \Rightarrow \Delta ABE \sim \Delta BDE\left( {g - g} ight) \hfill \\ \Rightarrow \dfrac{{AE}}{{BE}} = \dfrac{{BE}}{{DE}} \Rightarrow B{E^2} = AE.DE\left( 1 ight) \hfill \\ \end{matrix}

    Ta có: MB // AC 

    \Rightarrow \widehat {EMD} = \widehat {DCA}\left( {slt} ight)

    Mà \widehat {DCA} = \widehat {MAD} (góc nội tiếp và góc giữa tiếp tuyến và dây cung cùng chắn cung AD)

    => \widehat {EMD} = \widehat {MAD}

    Xét tam giác MEA và tam giác DEM ta có:

    Góc E là góc chung

    \widehat {EMD} = \widehat {MAD}

    \begin{matrix} \Rightarrow \Delta MEA \sim DEM \hfill \\ \Rightarrow \dfrac{{ME}}{{DE}} = \dfrac{{EA}}{{EM}} \Rightarrow E{M^2} = DE.EA\left( 2 ight) \hfill \\ \end{matrix}

    Từ (1) và (2) \Rightarrow E{M^2} = E{B^2} \Rightarrow EM = EB

  • Câu 4: Thông hiểu
    Chọn đáp án đúng

    Cho điểm C thuộc nửa đường tròn (O) đường kính AB. Từ điểm D thuộc đoạn AO kẻ đường thẳng vuông góc với AO cắt AC và BC lần lượt tại E và F. Tiếp tuyến tại C với nửa đường tròn cắt EF tại M và cắt AB tại N. Khi đó:

    Chọn đáp án đúng

    Hướng dẫn:

    Ta có: \widehat {MCA} = \frac{1}{2}sdAC (Góc giữa tiếp tuyến và dây cung chắn cung AC) (1)

    Ta laị có: 

    \begin{matrix} \widehat {MEC} = \widehat {AED} = {90^0} - \widehat {EAD} \hfill \\ = {90^0} - \dfrac{1}{2}sdBC = \dfrac{1}{2}sdAC\left( 2 ight) \hfill \\ \end{matrix}

    Từ (1) và (2) suy ra \widehat {MCE} = \widehat {MEC}

    Vậy tam giác MEC cân tại M

    => MC = MF

    Tương tự ta chứng minh MC = ME

    => ME = MF

  • Câu 5: Vận dụng
    Đặc điểm tam giác AMB

    Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại A. Gọi M là giao điểm của AO và BC. Khi đó tam giác AMB là:

    Hướng dẫn:

    Hình vẽ minh họa

    Đặc điểm tam giác AMB

    Xét đường tròn (O) có dây BC=R=OC=OB

    => Tam giác BOC là tam giác đều

    => \widehat {BOC} = {60^0} \Rightarrow sdBC = {60^0}

    Lại có: \widehat {ABC} là góc tạo bởi hai tiếp tuyến BA và dây cung BC của (O)

    Do góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn nên \widehat {ABC} = \frac{1}{2}sdBC = {30^0}

    Ta có:

    AB = AC (tia chất hai tiếp tuyến cắt nhau)

    OB = OC = R

    => AO là đường trung trực của BC

    => AO⊥BC tại M

    => \widehat {AMB} = {90^0} \Rightarrow \widehat {BAM} = {60^0}

    => Tam giác AMB vuông tại M và \widehat {ABM} = {30^0};\widehat {BAM} = {60^0}

    Ta lại có: \sin \widehat {ABM} = \frac{{AM}}{{AB}} \Rightarrow \sin {30^0} = \frac{{AM}}{{AB}} = \frac{1}{2}

    => Cạnh góc vuông AM bằng nửa cạnh huyền AB.

  • Câu 6: Thông hiểu
    Tính bán kính của đường tròn

    Tam giác ABC nội tiếp đường tròn (O; R) có AB = 8cm, AC = 15cm, đường cao AH = 5cm (H nằm ngoài đoạn BC). Bán kính R của đường tròn, tính bằng cm là:

    Hướng dẫn:

    Hình vẽ minh họa

    Tính bán kính của đường tròn

    Vẽ đường kính AD

    Ta có: \widehat {ACD} là góc nội tiếp chắn nửa đường tròn (O) 

    \Rightarrow \widehat {ACD} = {90^0}

    Ta có: \widehat {ADC};\widehat {ABC} là góc nội tiếp chắn cung AC

    \Rightarrow \widehat {ADC} = \widehat {ABC}

    Xét tam giác AHB và tam giác ACD ta có:

    \begin{matrix} \widehat {AHB} = \widehat {ACD} = {90^0} \hfill \\ \widehat {ADC} = \widehat {ABC}\left( {cmt} ight) \hfill \\ \Rightarrow \Delta AHB \sim \Delta ACD\left( {g - g} ight) \hfill \\ \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AB}}{{AD}} = \dfrac{{HB}}{{CD}} \hfill \\ \Rightarrow \dfrac{5}{{15}} = \dfrac{8}{{2R}} \Rightarrow R = 12\left( {cm} ight) \hfill \\ \end{matrix}

  • Câu 7: Thông hiểu
    Tính số đo cung BnC

    Số đo cung lớn BnC trong hình bên là:

    Tính số đo cung BnC

    Hướng dẫn:

    Ta có:

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {sdBmC + sdBnC = {{360}^0}} \\ {sdBmC = {{80}^0}} \end{array}} ight. \hfill \\ \Rightarrow sdBnC = {360^0} - sdBmC = {360^0} - {80^0} = {280^0} \hfill \\ \end{matrix}

  • Câu 8: Vận dụng
    Tìm quỹ tích điểm M

    Cho đường tròn tâm O và dây AB. Gọi M là trung điểm của dây AB. Cho A cố định. B di động trên (O). Hỏi M di động trên đường nào?

    Hướng dẫn:

    Hình vẽ minh họa

    Tìm quỹ tích điểm M

    Phần thuận:

    Giả sử M là trung điểm của dây AB. Ta có OM ⊥ AB (định lí)

    Khi B di động trên (O), điểm M luôn nhìn OA cố định dưới góc vuông

    => M thuộc đường tròn đường kính OA.

    Phần đảo:

    Lấy điểm M' bất kì trên đường tròn đường kính OA.

    Nối M' với A, đường thẳng M'A cắt đường tròn (O) tại B'.

    Nối M' với O ta có:

    \widehat {AM'O} = {90^0}

    => OM' ⊥ AB'

    => M' là trung điểm của AB'

    Kết luận: Tập hợp các trung điểm của dây AB là đường tròn đường kính OA.

  • Câu 9: Nhận biết
    Khẳng định nào đúng

    Đường tròn ngoại tiếp đa giác là đường tròn

    Hướng dẫn:

    Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp của đa giác.

  • Câu 10: Thông hiểu
    Bán kính đường tròn nội tiếp hình vuông

    Đường tròn nội tiếp hình vuông cạnh a có bán kính là

    Hướng dẫn:

    Hình vẽ minh họa

    Bán kính đường tròn nội tiếp hình vuông

    Gọi O là tâm của hình vuông ABCD; E; F; K; G là trung điểm của AD; DC; BC; AB

    Khi đó ta có: OE = OF = OK = OG = \dfrac{a}{2}

    => O là tâm đường tròn nội tiếp hình vuông ABCD

    => Bán kính đường tròn R = \frac{a}{2}

0/10
10 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (10%):
    2/3
  • Thông hiểu (50%):
    2/3
  • Vận dụng (40%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 19 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 9

Đăng nhập