Lớp 12 Toán 12

Bất phương trình lôgarit

Bài học Lí thuyết toán 12: Bất phương trình lôgarit giới thiệu cho các em khái niệm bất phương trình lôgarit cơ bản và cách giải bất phương trình lôgarit. Bên cạnh đó là các ví dụ bài tập có lời giải chi tiết giúp các em dễ dàng ôn tập củng cố.

1. Khái niệm

1.1. Định nghĩa

  • Bất phương trình lôgarit là bất phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
  • Bất phương trình logarit cơ bản có dạng {\log _a}x > b (hoặc {\log _a}x \geqslant b,{\log _a}x < b,{\log _a}x \leqslant b) với a > 0,a \ne 1
  • Để giải, ta xét bất phương trình {\log _a}x > b:

                     - Trường hợp a>1, ta có:

{\log _a}x > b \Leftrightarrow x > {a^b}

                     - Trường hợp 0 < a < 1, ta có:

{\log _a}x > b \Leftrightarrow 0 < x < {a^b}

Ví dụ: Điều kiện xác định của bất phương trình {\log _{\frac{1}{2}}}(4x + 2) - {\log _{\frac{1}{2}}}(x - 1) > lo{g_{\frac{1}{2}}}x là?

Giải:

BPT xác định khi: \left\{ \begin{gathered} x > 0 \hfill \\ 4x + 2 > 0 \hfill \\ x - 1 > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ x > - \frac{1}{2} \hfill \\ x > 1 \hfill \\ \end{gathered} \right. \Leftrightarrow x > 1.

1.2. Đồ thị minh họa

Ta minh họa bằng đồ thị như sau.

  • Với a>1, ta có đồ thị sau:

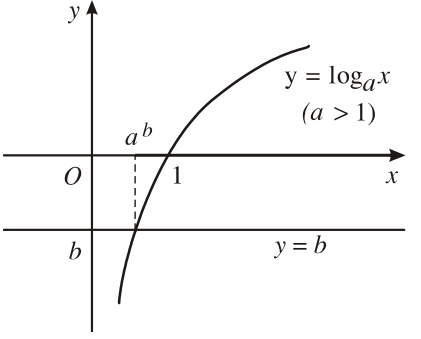
  • Với 0 < a < 1, ta có đồ thị sau:

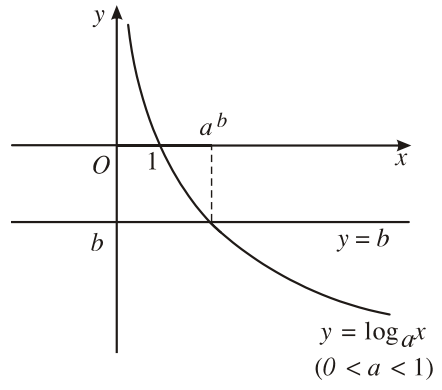
Quan sát đồ thị, ta thấy rằng:

  • Trường hợp : a>1: {\log _a}x > b khi và chỉ khi x > {a^b}
  • Trường hợp : 0 < a < 1: {\log _a}x > b khi và chỉ khi 0 < x < {a^b}.

2. Cách giải bất phương trình lôgarit

  • Đưa về cùng cơ số
    • Nếu a> 1 thì

{\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered} g(x) > 0 \hfill \\ f(x) > g(x) \hfill \\ \end{gathered} \right.

    • Nếu 0 < a < 1 thì

{\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered} f(x) > 0 \hfill \\ f(x) < g(x) \hfill \\ \end{gathered} \right.

  • Đặt ẩn phụ
  • Mũ hóa

Ví dụ: Tìm tập nghiệm của Bất phương trình {\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) \leqslant 2

Giải: 

+) Xét:   x > 0 \Rightarrow {2^x} > {2^0} = 1 \Rightarrow {2^x} + 1 > 2  \Rightarrow {\log _2}\left( {{2^x} + 1} \right) > {\log _2}2 = 1\left( 1 \right)

x > 0 \Rightarrow {4^x} > {4^0} = 1 \Rightarrow {4^x} + 2 > 2 + 1 = 3 \Rightarrow {\log _3}\left( {{4^x} + 2} \right) > {\log _3}3 = 1\left( 2 \right)

Cộng vế với vế của (1) và (2) ta được: {\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) > 2

Mà BPT: {\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) \leqslant 2 nên x > 0 (L)

+) Xét:    x \leqslant 0 \Rightarrow {2^x} \leqslant {2^0} = 1 \Rightarrow {2^x} + 1 \leqslant 2 \Rightarrow {\log _2}\left( {{2^x} + 1} \right) \leqslant {\log _2}2 = 1\left( 3 \right)

x \leqslant 0 \Rightarrow {4^x} \leqslant {4^0} = 1 \Rightarrow {4^x} + 2 \leqslant 2 + 1 = 3 \Rightarrow {\log _3}\left( {{4^x} + 2} \right) \leqslant {\log _3}3 = 1\left( 4 \right)

Cộng vế với vế của (3) và (4) ta được: {\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) \leqslant 2\left( {TM} \right)

Vậy x \leqslant 0 hay x \in \left( { - \infty ;0} \right].

Câu trắc nghiệm mã số: 1813,1812,1811,1809,1808,1807,1805,1749
  • 6 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12