Cho hình hộp chữ nhật OABC.DEFG có ![]() . Gọi L là tâm hình hộp. Biểu thị vectơ
. Gọi L là tâm hình hộp. Biểu thị vectơ ![]() theo ba vectơ
theo ba vectơ ![]() và
và ![]() ?
?
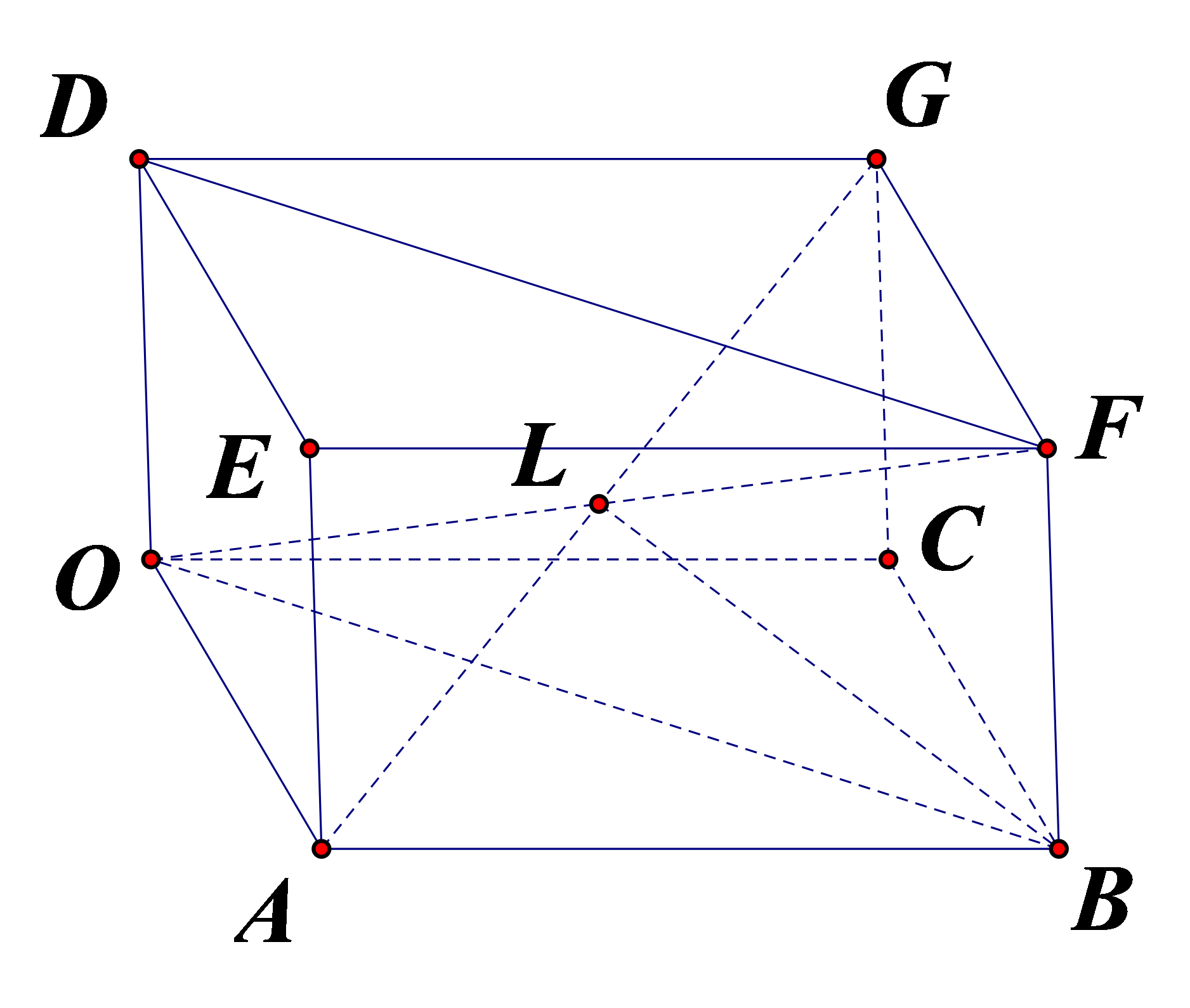
Vì I là tâm hình hộp theo giả thiết nên I là trung điểm đường chéo OF. Từ đây, suy ra
Cho hình hộp chữ nhật OABC.DEFG có ![]() . Gọi L là tâm hình hộp. Biểu thị vectơ
. Gọi L là tâm hình hộp. Biểu thị vectơ ![]() theo ba vectơ
theo ba vectơ ![]() và
và ![]() ?
?

Vì I là tâm hình hộp theo giả thiết nên I là trung điểm đường chéo OF. Từ đây, suy ra
Cho hình hộp ![]() Tìm hệ thức sai:
Tìm hệ thức sai:
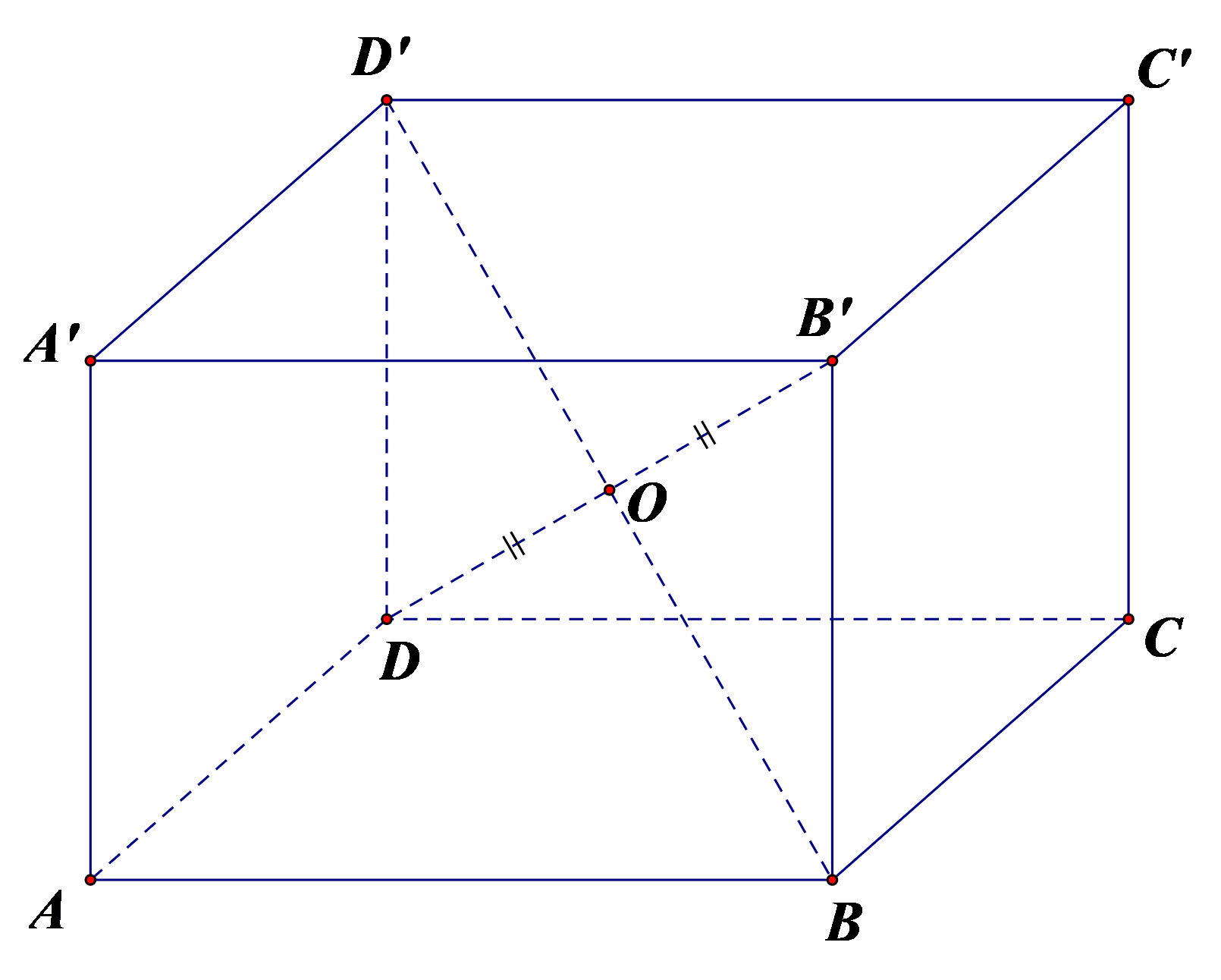
Gọi O là tâm hình hộp. Ta có:
Mặt khác ta được:
Từ đây suy ra:
Vậy là hệ thức sai và là đáp án cần chọn.
Cho khối tứ diện ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() .
.
Tìm hệ thức đúng:
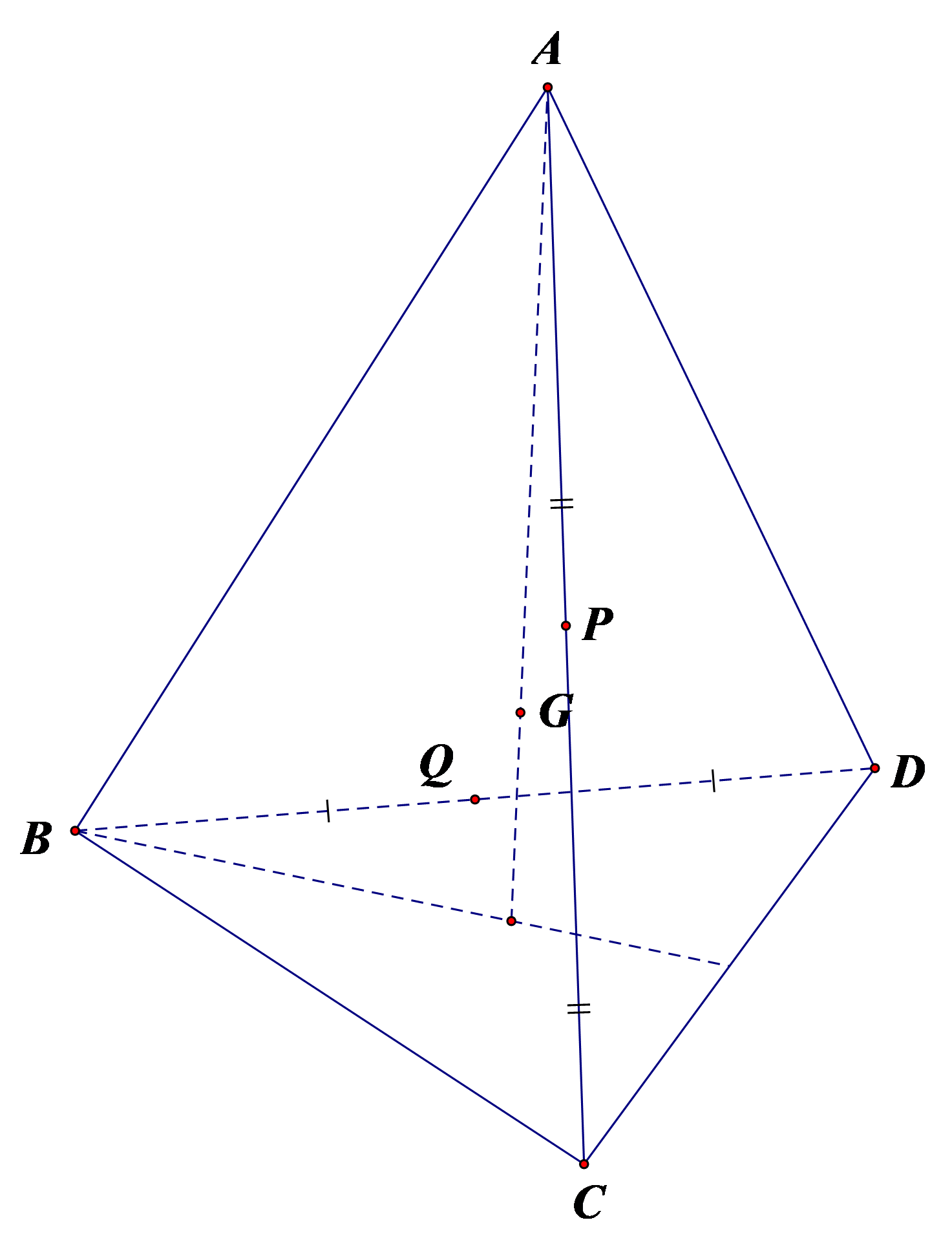
Theo đề bài, ta xét khối tứ diện ABCD, có:
(1)
(2)
Cộng từng vế của (1) cho (2), ta được:
Mà
Như vậy, .
Cho hai vectơ ![]() và
và ![]() với
với ![]() và
và ![]() .Tìm m để
.Tìm m để ![]() và
và ![]() vuông góc.
vuông góc.
Điều kiện để
vuông góc
Với
Cho tứ diện![]() .
. ![]() và
và ![]() lần lượt là trung điểm
lần lượt là trung điểm ![]() và
và ![]() . Chọn hệ thức sai:
. Chọn hệ thức sai:
Ta sẽ xét các đáp án:
Với (luôn đúng vì đây là hệ thức trung điểm)
Gọi P và Q lần lượt là trung điểm của AD và BC
là hình bình hành nên ta có:
Suy ra:(đúng)
Ta có: nên chọn đáp án sai là
(sai)
Với (đúng)
Cho ba điểm ![]() . Tính
. Tính ![]() để
để ![]() là trọng tâm tam giác ABC?
là trọng tâm tam giác ABC?
Vì G là trọng tâm tam giác ABC nên áp dụng công thức, ta có:
Thay tọa độ các điểm vào ta được hệ sau:
Trong không gian Oxyz cho tam giác ABC có G là trọng tâm của tam giác, biết ![]() .
.
Tìm tọa độ trọng tâm G của tam giác ABC đã cho?
Ta có nên suy ra được tọa độ điểm B và C tương ứng theo hệ sau là:
Vì G là trọng tâm của tam giác ABC nên ta có tọa độ điểm G là nghiệm của hệ:
Phân tích vectơ ![]() theo ba vectơ không đồng phẳng
theo ba vectơ không đồng phẳng
![]()
Ta có 3 vecto không đồng phẳng. Khi đó luôn có :
Trong không gian với hệ toạ độ ![]() , cho ba điểm
, cho ba điểm ![]() . Điểm M thuộc mặt phẳng
. Điểm M thuộc mặt phẳng ![]() và cách đều các điểm
và cách đều các điểm ![]() có tọa độ là:
có tọa độ là:
Gọi là điểm cần tìm.
Vì cách đều
nên ta có:
Vậy .
Tính góc của hai vectơ ![]()
Áp dụng công thức tính góc giữa 2 vecto, ta có:
Thay số suy ra được:
Trong không gian với hệ tọa độ ![]() , cho điểm
, cho điểm ![]() . Gọi
. Gọi ![]() là mặt phẳng đi qua điểm
là mặt phẳng đi qua điểm ![]() và cách gốc tọa độ
và cách gốc tọa độ ![]() một khoảng lớn nhất, mặt phẳng
một khoảng lớn nhất, mặt phẳng ![]() cắt các trục tọa độ tại các điểm
cắt các trục tọa độ tại các điểm ![]() . Tính thể tích khối chóp
. Tính thể tích khối chóp ![]() .
.
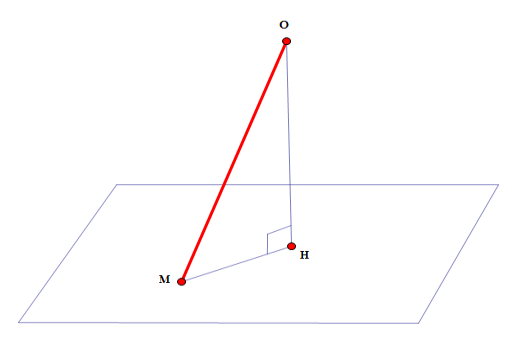
Gọi là hình chiếu của
lên
Tam giác có
Khi đó lớn nhất khi
, hay
.
Mp đi qua và nhận
làm véc tơ pháp tuyến,
phương trình :
cắt Ox, Oy, Oz lần lượt tại
=> Thể tích cần tìm là: .
Cho ba điểm ![]() . Tìm điểm E trên mặt phẳng
. Tìm điểm E trên mặt phẳng ![]() cách đều
cách đều ![]()
Gọi trên mặt phẳng
.
Ta có:
Cho ba điểm ![]() . Tìm tọa độ giao điểm của đường thẳng AB và mặt phẳng
. Tìm tọa độ giao điểm của đường thẳng AB và mặt phẳng ![]()
Gọi là giao điểm của đường thẳng AB và mặt phẳng (yOz).
Ta có và
cùng phương.
Cho ba điểm ![]() . Tìm tọa độ của C để ABC là tam giác đều?
. Tìm tọa độ của C để ABC là tam giác đều?
Áp dụng tích chất tam giác ABC đều có rồi xét hệ.
Tam giác ABC đều
Suy ra tọa độ điểm C là có 2 nghiệm C thỏa mãn:
Cho ba điểm ![]() . Tìm tọa độ của C để tam giác ABC là tam giác vuông cân tại A.
. Tìm tọa độ của C để tam giác ABC là tam giác vuông cân tại A.
Tam giác ABC vuông cân tại A
Trong không gian với hệ tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() và mặt
và mặt
cầu (S) tâm I(1;2;1), bán kính R. Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với
(S) tạo với nhau góc ![]() . Hãy viết phương trình mặt cầu (S)
. Hãy viết phương trình mặt cầu (S)
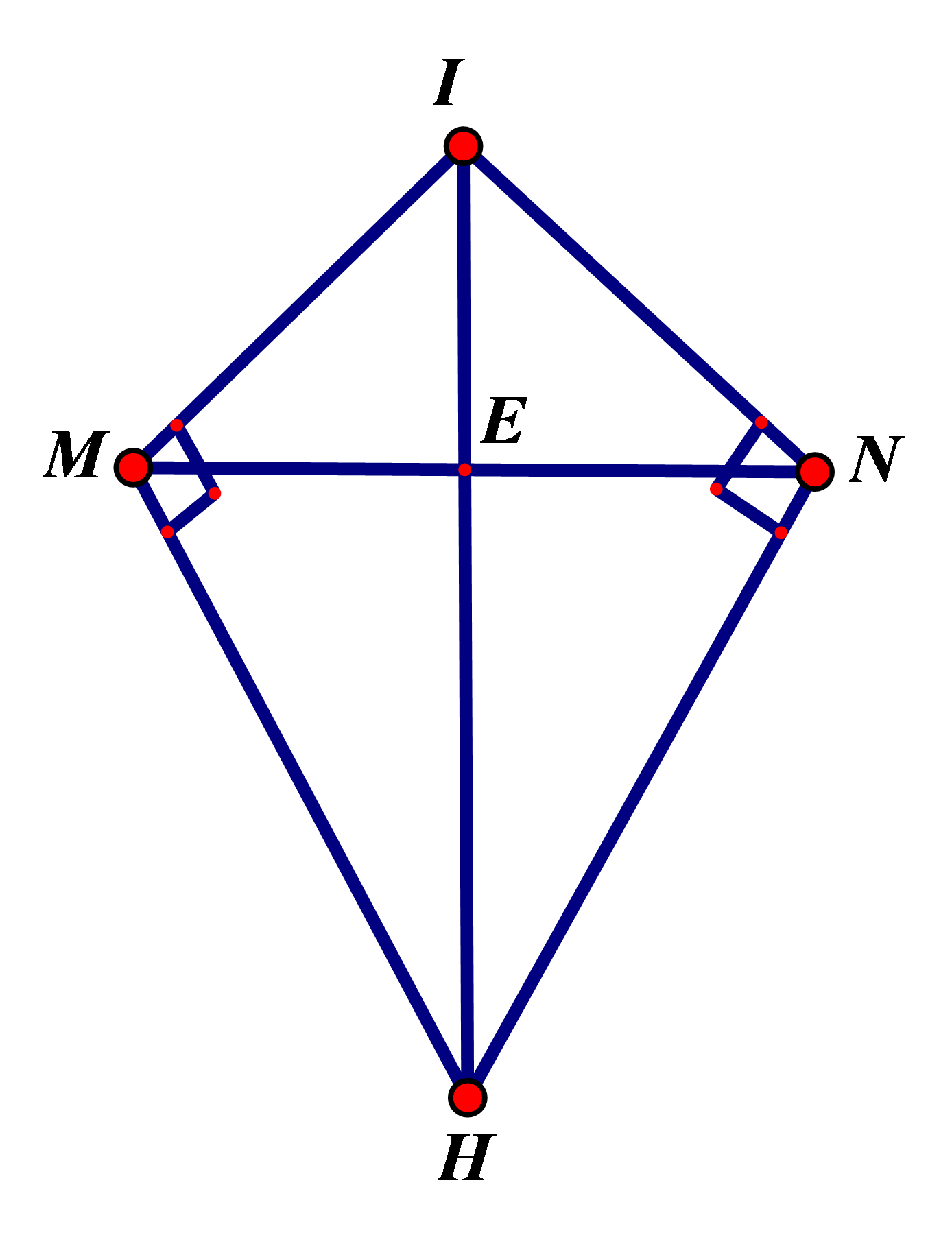
Gọi M, N là tiếp điểm của mặt phẳng (P), (Q) và mặt cầu (S). Gọi H là hình chiếu của điểm I trên đường thẳng d.
TH1: Góc :
Theo bài ra ta có:
TH2: Góc :
Theo bài ra ta có:
.
Cho 3 vectơ ![]() đều khác
đều khác ![]() . Ba vectơ
. Ba vectơ ![]() đồng phẳng khi và chỉ khi:
đồng phẳng khi và chỉ khi:
Áp dụng Điều kiện để 3 vecto đồng phẳng là:
Tính thể tích hình lăng trụ ABCD.EFGH, biết ![]() và
và ![]() .
.
Áp dụng công thức tính thể tích lăng trụ:
Theo đề bài, ta có:
Áp dụng CT tính thể tích khối lăng trụ:
Suy ra: .
Trong không gian Oxyz cho vectơ ![]() và
và ![]() . Gọi
. Gọi ![]() lần lượt là ba góc tạo bởi
lần lượt là ba góc tạo bởi ![]() với ba trục
với ba trục ![]() . Ta có:
. Ta có:
Áp dụng công thức hình chiếu vecto trên trục, ta có ngay được:
Cho M trên đường thẳng AB với ![]() và
và ![]() . Nếu
. Nếu ![]() với
với ![]() thì tọa độ của M là:
thì tọa độ của M là:
Vì M nằm trên AB và nên khi xét theo tọa độ vecto 2 điểm A và B, ta có:
