Cho hình phẳng ![]() giới hạn bởi đường cong
giới hạn bởi đường cong ![]() , trục hoành và các đường thẳng
, trục hoành và các đường thẳng ![]() . Khối tròn xoay tạo thành khi quay
. Khối tròn xoay tạo thành khi quay ![]() quanh trục hoành có thể tích
quanh trục hoành có thể tích ![]() là:
là:
Thể tích cần tính là:
Cho hình phẳng ![]() giới hạn bởi đường cong
giới hạn bởi đường cong ![]() , trục hoành và các đường thẳng
, trục hoành và các đường thẳng ![]() . Khối tròn xoay tạo thành khi quay
. Khối tròn xoay tạo thành khi quay ![]() quanh trục hoành có thể tích
quanh trục hoành có thể tích ![]() là:
là:
Thể tích cần tính là:
Tính tổng ![]()
Ta có:
Khi đó ta có:
Cho hàm số ![]() có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn ![]() và đồ thị hàm số
và đồ thị hàm số ![]() (như hình vẽ). biết
(như hình vẽ). biết ![]() và
và ![]() . Kết luận nào sau đây là đúng?
. Kết luận nào sau đây là đúng?
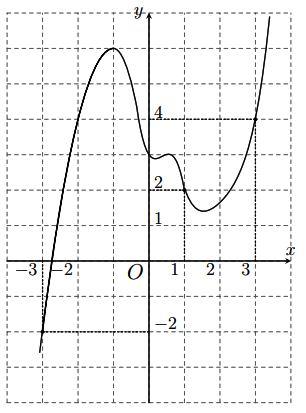
Hình vẽ minh họa:
Ta có:
Từ đồ thị ta thấy
Từ đồ thị ta thấy
=>
Mặt khác
Ta có bảng biến thiên như sau:
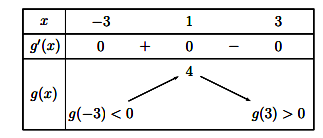
=> có duy nhất nghiệm trên
Tính thể tích của một vật thể nằm giữa hai mặt phẳng ![]() , biết thiết diện của vật thể cắt bởi mặt phẳng
, biết thiết diện của vật thể cắt bởi mặt phẳng ![]() vuông góc với trục
vuông góc với trục ![]() tại điểm có hoành độ là một tam giác đều có cạnh bằng
tại điểm có hoành độ là một tam giác đều có cạnh bằng ![]()
Diện tích thiết diện là
Ta có thể tích cần tính là
Cho hàm số ![]() có đạo hàm và liên tục trên
có đạo hàm và liên tục trên ![]() . Biết rằng đồ thị hàm số
. Biết rằng đồ thị hàm số ![]() như hình bên. Lập hàm số
như hình bên. Lập hàm số ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
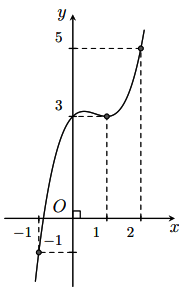
Hình vẽ minh họa:
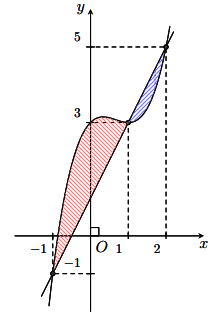
Đặt
Gọi là đồ thị của hàm số
Từ đồ thị ta thấy
Ta thấy
=> sai
=> đúng
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số ![]() , trục hoành và các đường thẳng
, trục hoành và các đường thẳng ![]()
Diện tích S của hình phẳng trên là:
Ta có:
=>
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và các đường thẳng
, trục hoành và các đường thẳng ![]()
Gọi S là diện tích của hình phẳng trên ta có:
Ta có:
Khi đó:
Một ô tô đang chạy đều với vận tốc ![]() thì người lái xe đạp phanh. Từ thời điểm ô tô chuyển động chậm dần đều với vận tốc
thì người lái xe đạp phanh. Từ thời điểm ô tô chuyển động chậm dần đều với vận tốc ![]() . Biết từ khi đạp phanh đến lúc dừng hẳn thì ô tô di chuyển được 56m. Tính giá trị của
. Biết từ khi đạp phanh đến lúc dừng hẳn thì ô tô di chuyển được 56m. Tính giá trị của ![]() ?
?
Khi dừng hẳn
Quãng đường xe đi được từ khi đạp phanh đến lúc dừng hẳn là:
Tính diện tích S của hình phẳng giới hạn bới đồ thị của hàm số ![]() và các đường thẳng
và các đường thẳng ![]() là:
là:
Ta có:
Phương trình hoành độ giao điểm của hai đồ thị là
Diện tích hình phẳng cần tìm là:
Cho hàm số ![]() liên tục và dương trên
liên tục và dương trên ![]() , hình phẳng giới hạn bởi các đường
, hình phẳng giới hạn bởi các đường ![]() , trục hoành và
, trục hoành và ![]() có diện tích bằng 5. Tính tích phân
có diện tích bằng 5. Tính tích phân 
Ta có:
Đặt ta được:
=>
Một ô tô xuất phát với vận tốc ![]() sau khi đi được một khoảng thời gian
sau khi đi được một khoảng thời gian ![]() thì bất ngờ phanh gấp với vận tốc
thì bất ngờ phanh gấp với vận tốc ![]() và đi thêm được một khoảng thời gian
và đi thêm được một khoảng thời gian ![]() nữa thì dừng lại. Hỏi từ khi xuất phát đến lúc dừng lại thì ô tô đã đi được bao nhiêu mét?
nữa thì dừng lại. Hỏi từ khi xuất phát đến lúc dừng lại thì ô tô đã đi được bao nhiêu mét?
Ta có: do đó khi gặp chướng ngại vật vật có vận tốc là
=>
Vật dừng lại khi
Quãng đường vật đi được là
Tính diện tích hình phẳng giới hạn bởi ![]()
Xét phương trình hoành độ giao điểm ta có:
Diện tích hình phẳng cần tính là:
Một bể thủy tinh chứa nước có thiết diện ngang (mặt trong của thùng) là một đường elip có trục lớn bằng 1m, trục bé bằng 0,8m, chiều dài bằng 3m nằm trong của thùng. Bể nước được đặt sao cho trục bé nằm theo phương thẳng đúng (như hình vẽ). Tính thể tích V của nước có trong bể, biết chiều cao nước trong bể là 0,6m. (Kết quả được làm tròn đến phần trăm).
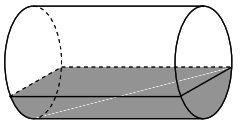
Xét một đáy của bể và gắn hệ trục tọa độ như hình vẽ:
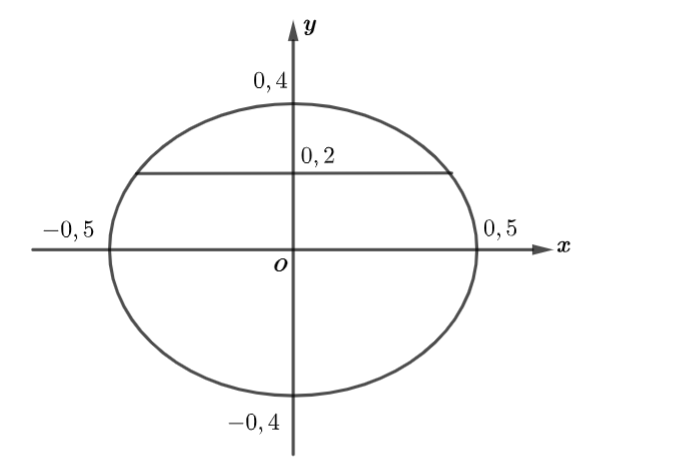
Phương trình đường elip đáy khi đó có phương trình
Khi đó chiều cao của mép nước trong bể với đường thẳng
Xét phương trình
Diện tích phần mặt chứa nước là:
Do đó thể tích nước trong thùng là:
Một ô tô đang chạy với vận tốc ![]() thì dừng lái đạp phanh. Sau khi đạp phanh, ô tô di chuyển động chậm dần đều với vận tốc
thì dừng lái đạp phanh. Sau khi đạp phanh, ô tô di chuyển động chậm dần đều với vận tốc ![]() , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?
, trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?
Khi dừng hẳn
Quãng đường xe đi được từ khi đạp phan đến lúc dừng hẳn là:
Một chất điểm dạng chuyển động với vận tốc ![]() thì tăng tốc với gia tốc
thì tăng tốc với gia tốc ![]() . Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3s kể từ lúc bắt đầu tăng tốc.
. Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3s kể từ lúc bắt đầu tăng tốc.
Ta có:
Do khi bắt đầu tăng tốc nên
Khi đó quãng đường xe đi được sau 3 giây kể từ khi ô tô tăng tốc bằng:
Cho hình phẳng ![]() giới hạn với các đường
giới hạn với các đường ![]() . Tính thể tích
. Tính thể tích ![]() của khối tròn xoay thu được khi
của khối tròn xoay thu được khi ![]() quay quanh trục
quay quanh trục ![]() ?
?
Thể tích cần tìm là:
Viết công thức tính thể tích ![]() của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số
của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số ![]() , trục
, trục ![]() và hai đường thẳng
và hai đường thẳng ![]() xung quanh trục
xung quanh trục ![]() .
.
Thể tích của khối tròn xoay cần tính là:
Tốc độ tăng trưởng bán kính của thân cây được tính bằng công thức ![]() , trong đó
, trong đó ![]() là thời gian khảo sát (tính theo năm), là thời điểm đầu khảo sát,
là thời gian khảo sát (tính theo năm), là thời điểm đầu khảo sát, ![]() là bán kính của thân cây tại thời điểm
là bán kính của thân cây tại thời điểm ![]() và
và ![]() . Tính bán kính của thân cây sau 20 năm kể từ lúc bắt đầu khảo sát, biết rằng bán kính cây tại thời điểm bắt đầu khảo sát là 5cm.
. Tính bán kính của thân cây sau 20 năm kể từ lúc bắt đầu khảo sát, biết rằng bán kính cây tại thời điểm bắt đầu khảo sát là 5cm.
Ta có:
Từ giả thiết ta có:
=>
Sau 5 năm bán kính thân cây bằng
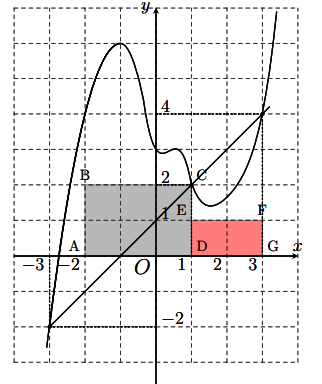
Trong hệ trục tọa độ Oxy, cho parabol ![]() và hai đường thẳng
và hai đường thẳng ![]() (mô tả như hình vẽ). Gọi
(mô tả như hình vẽ). Gọi ![]() là diện tích hình phẳng giới hạn bới và đường thẳng
là diện tích hình phẳng giới hạn bới và đường thẳng ![]() (phần tô màu đen);
(phần tô màu đen); ![]() là diện tích hình phẳng giới hạn bới parabol
là diện tích hình phẳng giới hạn bới parabol ![]() và đường thẳng
và đường thẳng ![]() (phần gạch chéo). Với điều kiện nào sau đây của
(phần gạch chéo). Với điều kiện nào sau đây của ![]() thì
thì ![]() ?
?
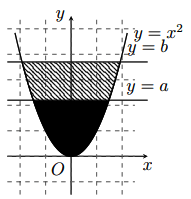
Phương trình hoành độ giao điểm của và đường thẳng
là:
Phương trình hoành độ giao điểm của và đường thẳng
là:
Diện tích hình phẳng giới hạn bởi và
là:
Diện tích hình phẳng giới hạn bởi và
là:
Khi đó:
Cho đường cong (C) ![]() . Xét điểm A có hoành độ dương thuộc (C), tiếp tuyến của (C) tại A tạo với (C) một hình phẳng có diện tích bằng 27. Hoành độ điểm A thuộc khoảng nào dưới đây?
. Xét điểm A có hoành độ dương thuộc (C), tiếp tuyến của (C) tại A tạo với (C) một hình phẳng có diện tích bằng 27. Hoành độ điểm A thuộc khoảng nào dưới đây?
Ta có:
Ta có:
Phương trình tiếp tuyến d của (C) tại A là
Ta có phương trình hoành độ giao điểm d và (C) là:
Gọi S là diện tích của hình phẳng giới hạn bởi tiếp tuyến d và (C).
Ta có:
