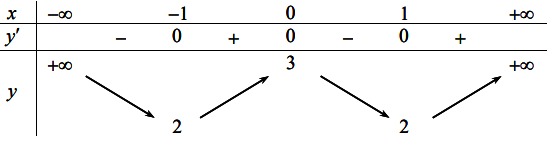
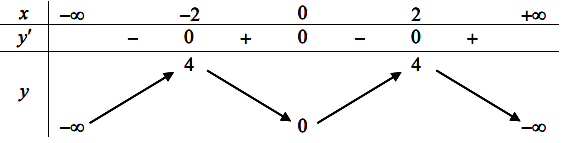
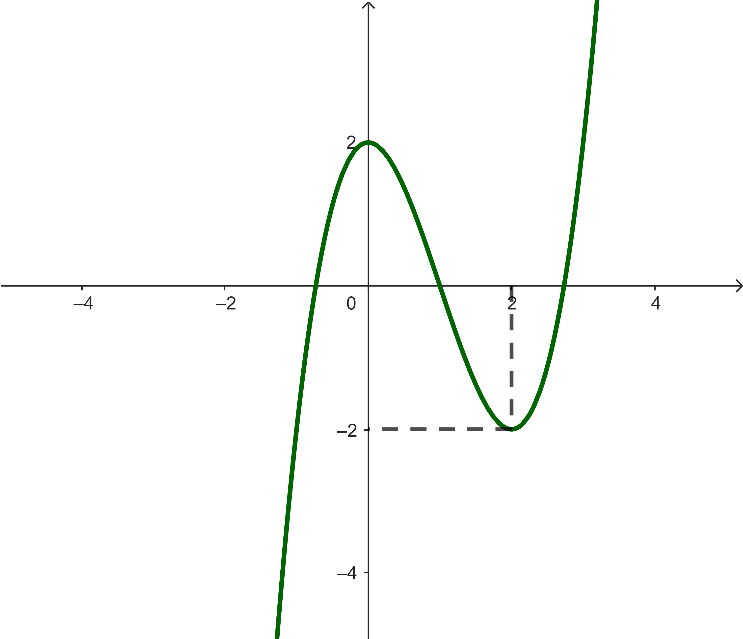
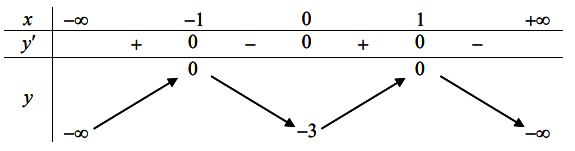
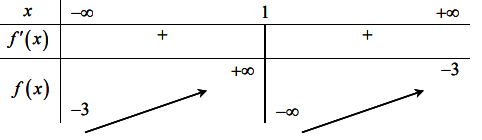
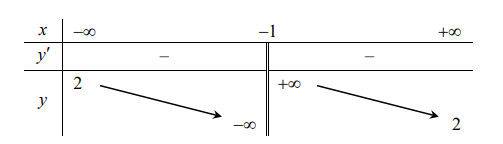
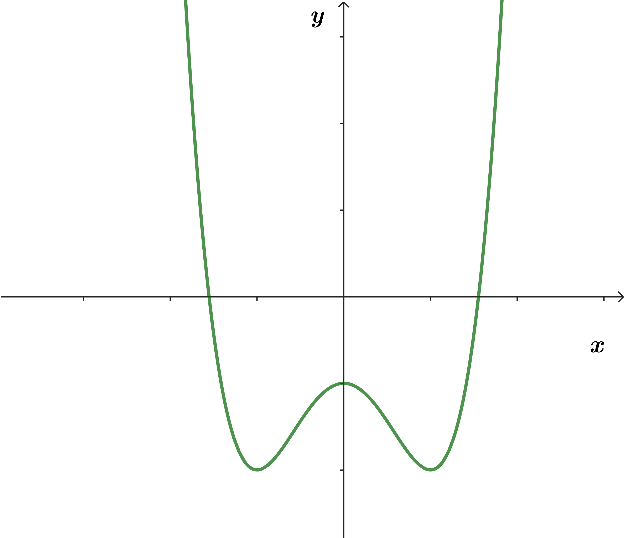
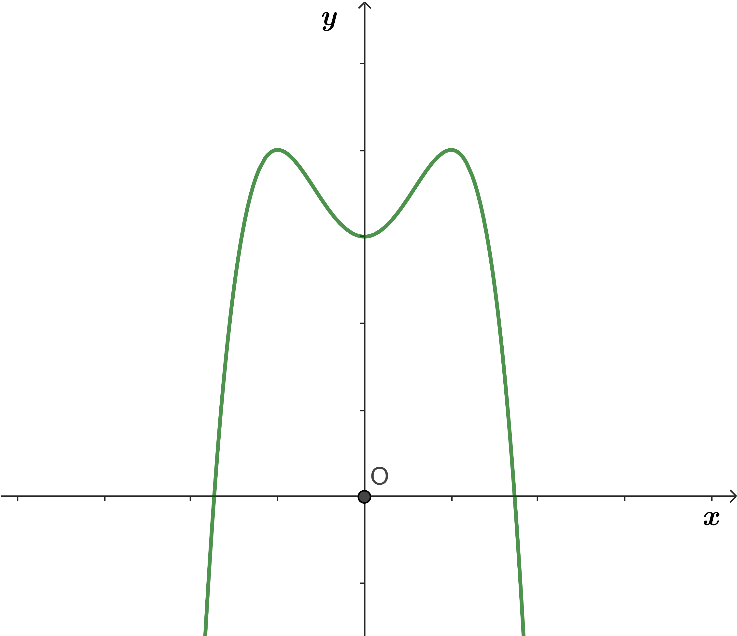
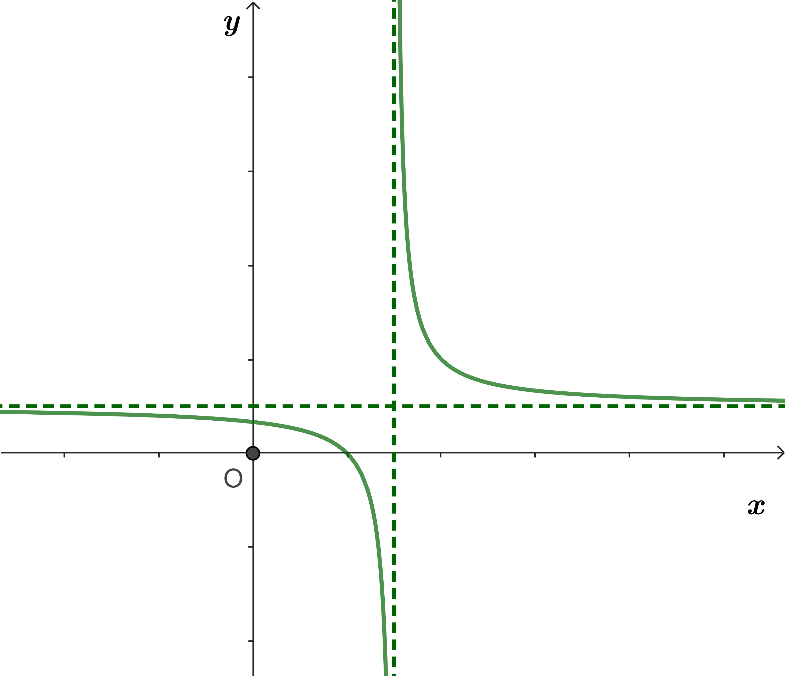
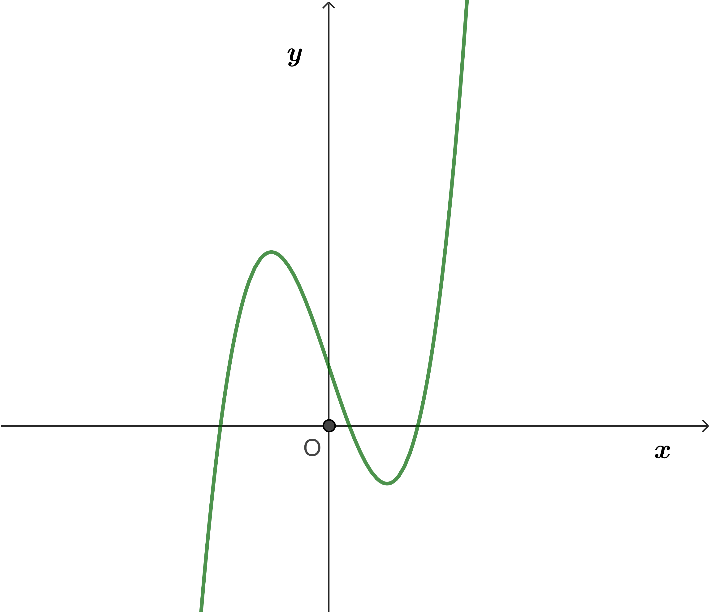
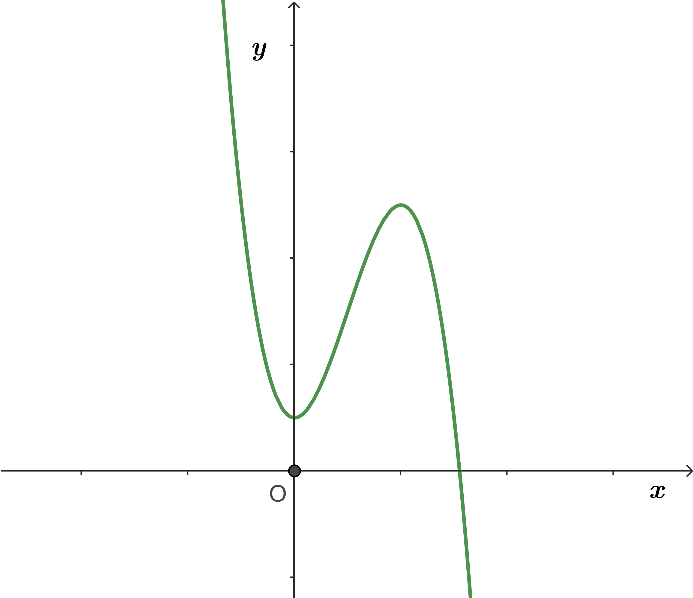
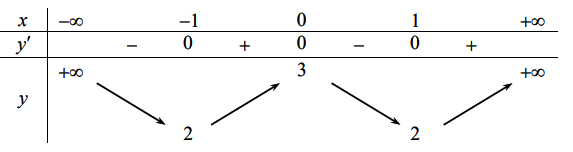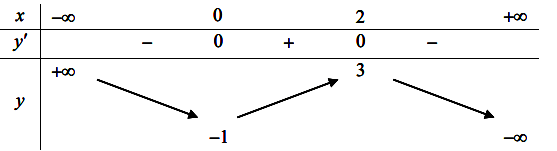Cho hàm số y = f(x) liên tục trên ![]() và có bảng biến thiên như hình vẽ dưới đây
và có bảng biến thiên như hình vẽ dưới đây
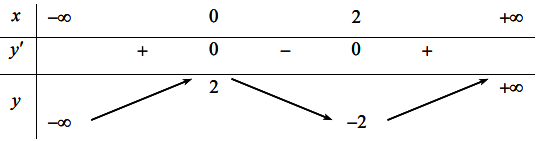
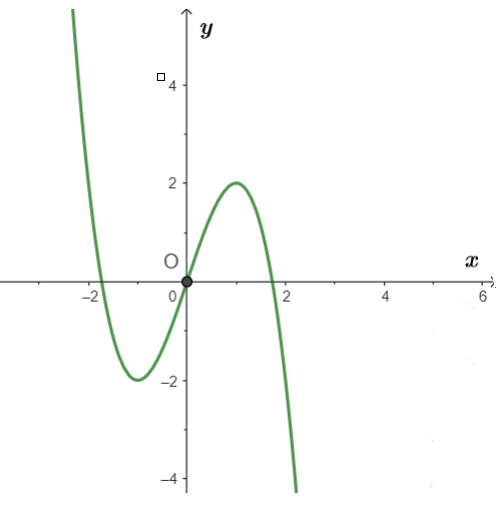
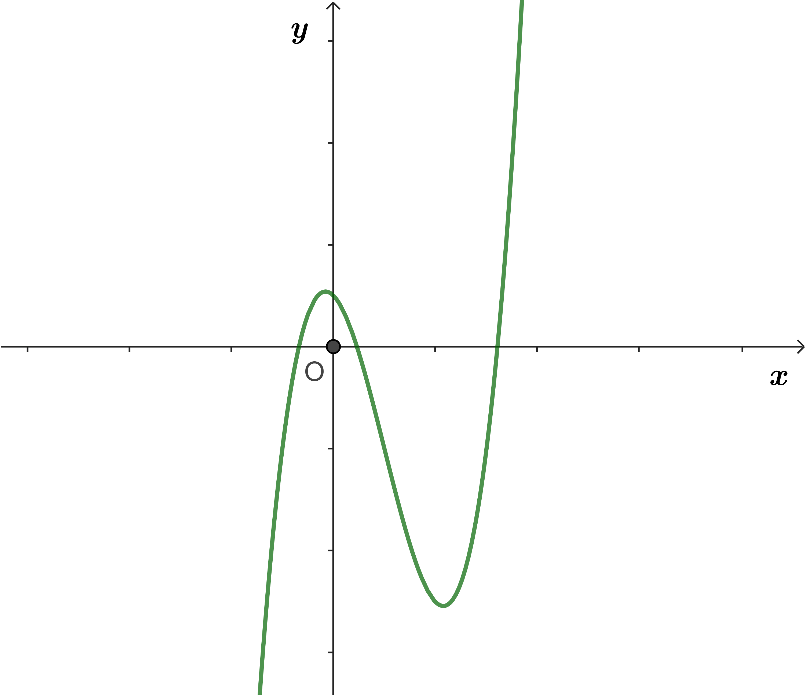
Hàm số y = f(x) là hàm số nào trong các hàm số sau:
Dựa vào bảng biến thiên ta thấy:
=> Hệ số a > 0
=> Loại đáp án B và C
Mặt khác hàm số đạt cực trị tại x = 0 và x = 2
=> Loại đáp án D